BEGAN: Boundary Equilibrium Generative Adversarial Networks
David Berthelot and Thomas Schumm and Luke Metz
arXiv e-Print archive - 2017 via Local arXiv
Keywords: cs.LG, stat.ML
First published: 2017/03/31 (7 years ago)
Abstract: We propose a new equilibrium enforcing method paired with a loss derived from the Wasserstein distance for training auto-encoder based Generative Adversarial Networks. This method balances the generator and discriminator during training. Additionally, it provides a new approximate convergence measure, fast and stable training and high visual quality. We also derive a way of controlling the trade-off between image diversity and visual quality. We focus on the image generation task, setting a new milestone in visual quality, even at higher resolutions. This is achieved while using a relatively simple model architecture and a standard training procedure.
more
less
David Berthelot and Thomas Schumm and Luke Metz
arXiv e-Print archive - 2017 via Local arXiv
Keywords: cs.LG, stat.ML
First published: 2017/03/31 (7 years ago)
Abstract: We propose a new equilibrium enforcing method paired with a loss derived from the Wasserstein distance for training auto-encoder based Generative Adversarial Networks. This method balances the generator and discriminator during training. Additionally, it provides a new approximate convergence measure, fast and stable training and high visual quality. We also derive a way of controlling the trade-off between image diversity and visual quality. We focus on the image generation task, setting a new milestone in visual quality, even at higher resolutions. This is achieved while using a relatively simple model architecture and a standard training procedure.
|
[link]
* [Detailed Summary](https://blog.heuritech.com/2017/04/11/began-state-of-the-art-generation-of-faces-with-generative-adversarial-networks/)
* [Tensorflow implementation](https://github.com/carpedm20/BEGAN-tensorflow)
### Summary
* They suggest a GAN algorithm that is based on an autoencoder with Wasserstein distance.
* Their method generates highly realistic human faces.
* Their method has a convergence measure, which reflects the quality of the generates images.
* Their method has a diversity hyperparameter, which can be used to set the tradeoff between image diversity and image quality.
### How
* Like other GANs, their method uses a generator G and a discriminator D.
* Generator
* The generator is fairly standard.
* It gets a noise vector `z` as input and uses upsampling+convolutions to generate images.
* It uses ELUs and no BN.
* Discriminator
* The discriminator is a full autoencoder (i.e. it converts input images to `8x8x3` tensors, then reconstructs them back to images).
* It has skip-connections from the `8x8x3` layer to each upsampling layer.
* It also uses ELUs and no BN.
* Their method now has the following steps:
1. Collect real images `x_real`.
2. Generate fake images `x_fake = G(z)`.
3. Reconstruct the real images `r_real = D(x_real)`.
4. Reconstruct the fake images `r_fake = D(x_fake)`.
5. Using an Lp-Norm (e.g. L1-Norm), compute the reconstruction loss of real images `d_real = Lp(x_real, r_real)`.
6. Using an Lp-Norm (e.g. L1-Norm), compute the reconstruction loss of fake images `d_fake = Lp(x_fake, r_fake)`.
7. The loss of D is now `L_D = d_real - d_fake`.
8. The loss of G is now `L_G = -L_D`.
* About the loss
* `r_real` and `r_fake` are really losses (e.g. L1-loss or L2-loss). In the paper they use `L(...)` for that. Here they are referenced as `d_*` in order to avoid confusion.
* The loss `L_D` is based on the Wasserstein distance, as in WGAN.
* `L_D` assumes, that the losses `d_real` and `d_fake` are normally distributed and tries to move their mean values. Ideally, the discriminator produces very different means for real/fake images, while the generator leads to very similar means.
* Their formulation of the Wasserstein distance does not require K-Lipschitz functions, which is why they don't have the weight clipping from WGAN.
* Equilibrium
* The generator and discriminator are at equilibrium, if `E[r_fake] = E[r_real]`. (That's undesirable, because it means that D can't differentiate between fake and real images, i.e. G doesn't get a proper gradient any more.)
* Let `g = E[r_fake] / E[r_real]`, then:
* Low `g` means that `E[r_fake]` is low and/or `E[r_real]` is high, which means that real images are not as well reconstructed as fake images. This means, that the discriminator will be more heavily trained towards reconstructing real images correctly (as that is the main source of error).
* High `g` conversely means that real images are well reconstructed (compared to fake ones) and that the discriminator will be trained more towards fake ones.
* `g` gives information about how much G and D should be trained each (so that none of the two overwhelms the other).
* They introduce a hyperparameter `gamma` (from interval `[0,1]`), which reflects the target value of the balance `g`.
* Using `gamma`, they change their losses `L_D` and `L_G` slightly:
* `L_D = d_real - k_t d_fake`
* `L_G = r_fake`
* `k_t+1 = k_t + lambda_k (gamma d_real - d_fake)`.
* `k_t` is a control term that controls how much D is supposed to focus on the fake images. It changes with every batch.
* `k_t` is clipped to `[0,1]` and initialized at `0` (max focus on reconstructing real images).
* `lambda_k` is like the learning rate of the control term, set to `0.001`.
* Note that `gamma d_real - d_fake = 0 <=> gamma d_real = d_fake <=> gamma = d_fake / d_real`.
* Convergence measure
* They measure the convergence of their model using `M`:
* `M = d_real + |gamma d_real - d_fake|`
* `M` goes down, if `d_real` goes down (D becomes better at autoencoding real images).
* `M` goes down, if the difference in reconstruction error between real and fake images goes down, i.e. if G becomes better at generating fake images.
* Other
* They use Adam with learning rate 0.0001. They decrease it by a factor of 2 whenever M stalls.
* Higher initial learning rate could lead to model collapse or visual artifacs.
* They generate images of max size 128x128.
* They don't use more than 128 filters per conv layer.
### Results
* NOTES:
* Below example images are NOT from generators trained on CelebA. They used a custom dataset of celebrity images. They don't show any example images from the dataset. The generated images look like there is less background around the faces, making the task easier.
* Few example images. Unclear how much cherry picking was involved. Though the results from the tensorflow example (see like at top) make it look like the examples are representative (aside from speckle-artifacts).
* No LSUN Bedrooms examples. Human faces are comparatively easy to generate.
* Example images at 128x128:
* 
* Effect of changing the target balance `gamma`:
* 
* High gamma leads to more diversity at lower quality.
* Interpolations:
* 
* Convergence measure `M` and associated image quality during the training:
* 
 |
StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks
Zhang, Han and Xu, Tao and Li, Hongsheng and Zhang, Shaoting and Huang, Xiaolei and Wang, Xiaogang and Metaxas, Dimitris N.
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Zhang, Han and Xu, Tao and Li, Hongsheng and Zhang, Shaoting and Huang, Xiaolei and Wang, Xiaogang and Metaxas, Dimitris N.
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They propose a two-stage GAN architecture that generates 256x256 images of (relatively) high quality.
* The model gets text as an additional input and the images match the text.
### How
* Most of the architecture is the same as in any GAN:
* Generator G generates images.
* Discriminator D discriminates betweens fake and real images.
* G gets a noise variable `z`, so that it doesn't always do the same thing.
* Two-staged image generation:
* Instead of one step, as in most GANs, they use two steps, each consisting of a G and D.
* The first generator creates 64x64 images via upsampling.
* The first discriminator judges these images via downsampling convolutions.
* The second generator takes the image from the first generator, downsamples it via convolutions, then applies some residual convolutions and then re-upsamples it to 256x256.
* The second discriminator is comparable to the first one (downsampling convolutions).
* Note that the second generator does not get an additional noise term `z`, only the first one gets it.
* For upsampling, they use 3x3 convolutions with ReLUs, BN and nearest neighbour upsampling.
* For downsampling, they use 4x4 convolutions with stride 2, Leaky ReLUs and BN (the first convolution doesn't seem to use BN).
* Text embedding:
* The generated images are supposed to match input texts.
* These input texts are embedded to vectors.
* These vectors are added as:
1. An additional input to the first generator.
2. An additional input to the second generator (concatenated after the downsampling and before the residual convolutions).
3. An additional input to the first discriminator (concatenated after the downsampling).
4. An additional input to the second discriminator (concatenated after the downsampling).
* In case the text embeddings need to be matrices, the values are simply reshaped to `(N, 1, 1)` and then repeated to `(N, H, W)`.
* The texts are converted to embeddings via a network at the start of the model.
* Input to that vector: Unclear. (Concatenated word vectors? Seems to not be described in the text.)
* The input is transformed to a vector via a fully connected layer (the text model is apparently not recurrent).
* The vector is transformed via fully connected layers to a mean vector and a sigma vector.
* These are then interpreted as normal distributions, from which the final output vector is sampled. This uses the reparameterization trick, similar to the method in VAEs.
* Just like in VAEs, a KL-divergence term is added to the loss, which prevents each single normal distribution from deviating too far from the unit normal distribution `N(0,1)`.
* The authors argue, that using the VAE-like formulation -- instead of directly predicting an output vector (via FC layers) -- compensated for the lack of labels (smoother manifold).
* Note: This way of generating text embeddings seems very simple. (No recurrence, only about two layers.) It probably won't do much more than just roughly checking for the existence of specific words and word combinations (e.g. "red head").
* Visualization of the architecture:
* 
### Results
* Note: No example images of the two-stage architecture for LSUN bedrooms.
* Using only the first stage of the architecture (first G and D) reduces the Inception score significantly.
* Adding the text to both the first and second generator improves the Inception score slightly.
* Adding the VAE-like text embedding generation (as opposed to only FC layers) improves the Inception score slightly.
* Generating images at higher resolution (256x256 instead of 128x128) improves the Inception score significantly
* Note: The 256x256 architecture has more residual convolutions than the 128x128 one.
* Note: The 128x128 and the 256x256 are both upscaled to 299x299 images before computing the Inception score. That should make the 128x128 images quite blurry and hence of low quality.
* Example images, with text and stage 1/2 results:
* 
* More examples of birds:
* 
* Examples of failures:
* 
* The authors argue, that most failure cases happen when stage 1 messes up.
 |
Self-Normalizing Neural Networks
Günter Klambauer and Thomas Unterthiner and Andreas Mayr and Sepp Hochreiter
arXiv e-Print archive - 2017 via Local arXiv
Keywords: cs.LG, stat.ML
First published: 2017/06/08 (6 years ago)
Abstract: Deep Learning has revolutionized vision via convolutional neural networks (CNNs) and natural language processing via recurrent neural networks (RNNs). However, success stories of Deep Learning with standard feed-forward neural networks (FNNs) are rare. FNNs that perform well are typically shallow and, therefore cannot exploit many levels of abstract representations. We introduce self-normalizing neural networks (SNNs) to enable high-level abstract representations. While batch normalization requires explicit normalization, neuron activations of SNNs automatically converge towards zero mean and unit variance. The activation function of SNNs are "scaled exponential linear units" (SELUs), which induce self-normalizing properties. Using the Banach fixed-point theorem, we prove that activations close to zero mean and unit variance that are propagated through many network layers will converge towards zero mean and unit variance -- even under the presence of noise and perturbations. This convergence property of SNNs allows to (1) train deep networks with many layers, (2) employ strong regularization, and (3) to make learning highly robust. Furthermore, for activations not close to unit variance, we prove an upper and lower bound on the variance, thus, vanishing and exploding gradients are impossible. We compared SNNs on (a) 121 tasks from the UCI machine learning repository, on (b) drug discovery benchmarks, and on (c) astronomy tasks with standard FNNs and other machine learning methods such as random forests and support vector machines. SNNs significantly outperformed all competing FNN methods at 121 UCI tasks, outperformed all competing methods at the Tox21 dataset, and set a new record at an astronomy data set. The winning SNN architectures are often very deep. Implementations are available at: github.com/bioinf-jku/SNNs.
more
less
Günter Klambauer and Thomas Unterthiner and Andreas Mayr and Sepp Hochreiter
arXiv e-Print archive - 2017 via Local arXiv
Keywords: cs.LG, stat.ML
First published: 2017/06/08 (6 years ago)
Abstract: Deep Learning has revolutionized vision via convolutional neural networks (CNNs) and natural language processing via recurrent neural networks (RNNs). However, success stories of Deep Learning with standard feed-forward neural networks (FNNs) are rare. FNNs that perform well are typically shallow and, therefore cannot exploit many levels of abstract representations. We introduce self-normalizing neural networks (SNNs) to enable high-level abstract representations. While batch normalization requires explicit normalization, neuron activations of SNNs automatically converge towards zero mean and unit variance. The activation function of SNNs are "scaled exponential linear units" (SELUs), which induce self-normalizing properties. Using the Banach fixed-point theorem, we prove that activations close to zero mean and unit variance that are propagated through many network layers will converge towards zero mean and unit variance -- even under the presence of noise and perturbations. This convergence property of SNNs allows to (1) train deep networks with many layers, (2) employ strong regularization, and (3) to make learning highly robust. Furthermore, for activations not close to unit variance, we prove an upper and lower bound on the variance, thus, vanishing and exploding gradients are impossible. We compared SNNs on (a) 121 tasks from the UCI machine learning repository, on (b) drug discovery benchmarks, and on (c) astronomy tasks with standard FNNs and other machine learning methods such as random forests and support vector machines. SNNs significantly outperformed all competing FNN methods at 121 UCI tasks, outperformed all competing methods at the Tox21 dataset, and set a new record at an astronomy data set. The winning SNN architectures are often very deep. Implementations are available at: github.com/bioinf-jku/SNNs.
|
[link]
https://github.com/bioinf-jku/SNNs
* They suggest a variation of ELUs, which leads to networks being automatically normalized.
* The effects are comparable to Batch Normalization, while requiring significantly less computation (barely more than a normal ReLU).
### How
* They define Self-Normalizing Neural Networks (SNNs) as neural networks, which automatically keep their activations at zero-mean and unit-variance (per neuron).
* SELUs
* They use SELUs to turn their networks into SNNs.
* Formula:
* 
* with `alpha = 1.6733` and `lambda = 1.0507`.
* They proof that with properly normalized weights the activations approach a fixed point of zero-mean and unit-variance. (Different settings for alpha and lambda can lead to other fixed points.)
* They proof that this is still the case when previous layer activations and weights do not have optimal values.
* They proof that this is still the case when the variance of previous layer activations is very high or very low and argue that the mean of those activations is not so important.
* Hence, SELUs with these hyperparameters should have self-normalizing properties.
* SELUs are here used as a basis because:
1. They can have negative and positive values, which allows to control the mean.
2. They have saturating regions, which allows to dampen high variances from previous layers.
3. They have a slope larger than one, which allows to increase low variances from previous layers.
4. They generate a continuous curve, which ensures that there is a fixed point between variance damping and increasing.
* ReLUs, Leaky ReLUs, Sigmoids and Tanhs do not offer the above properties.
* Initialization
* SELUs for SNNs work best with normalized weights.
* They suggest to make sure per layer that:
1. The first moment (sum of weights) is zero.
2. The second moment (sum of squared weights) is one.
* This can be done by drawing weights from a normal distribution `N(0, 1/n)`, where `n` is the number of neurons in the layer.
* Alpha-dropout
* SELUs don't perform as well with normal Dropout, because their point of low variance is not 0.
* They suggest a modification of Dropout called Alpha-dropout.
* In this technique, values are not dropped to 0 but to `alpha' = -lambda * alpha = -1.0507 * 1.6733 = -1.7581`.
* Similar to dropout, activations are changed during training to compensate for the dropped units.
* Each activation `x` is changed to `a(xd+alpha'(1-d))+b`.
* `d = B(1, q)` is the dropout variable consisting of 1s and 0s.
* `a = (q + alpha'^2 q(1-q))^(-1/2)`
* `b = -(q + alpha'^2 q(1-q))^(-1/2) ((1-q)alpha')`
* They made good experiences with dropout rates around 0.05 to 0.1.
### Results
* Note: All of their tests are with fully connected networks. No convolutions.
* Example training results:
* 
* Left: MNIST, Right: CIFAR10
* Networks have N layers each, see legend. No convolutions.
* 121 UCI Tasks
* They manage to beat SVMs and RandomForests, while other networks (Layer Normalization, BN, Weight Normalization, Highway Networks, ResNet) perform significantly worse than their network (and usually don't beat SVMs/RFs).
* Tox21
* They achieve better results than other networks (again, Layer Normalization, BN, etc.).
* They achive almost the same result as the so far best model on the dataset, which consists of a mixture of neural networks, SVMs and Random Forests.
* HTRU2
* They achieve better results than other networks.
* They beat the best non-neural method (Naive Bayes).
* Among all tested other networks, MSRAinit performs best, which references a network withput any normalization, only ReLUs and Microsoft Weight Initialization (see paper: `Delving deep into rectifiers: Surpassing human-level performance on imagenet classification`).
 |
Wasserstein GAN
Martin Arjovsky and Soumith Chintala and Léon Bottou
arXiv e-Print archive - 2017 via Local arXiv
Keywords: stat.ML, cs.LG
First published: 2017/01/26 (7 years ago)
Abstract: We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learning curves useful for debugging and hyperparameter searches. Furthermore, we show that the corresponding optimization problem is sound, and provide extensive theoretical work highlighting the deep connections to other distances between distributions.
more
less
Martin Arjovsky and Soumith Chintala and Léon Bottou
arXiv e-Print archive - 2017 via Local arXiv
Keywords: stat.ML, cs.LG
First published: 2017/01/26 (7 years ago)
Abstract: We introduce a new algorithm named WGAN, an alternative to traditional GAN training. In this new model, we show that we can improve the stability of learning, get rid of problems like mode collapse, and provide meaningful learning curves useful for debugging and hyperparameter searches. Furthermore, we show that the corresponding optimization problem is sound, and provide extensive theoretical work highlighting the deep connections to other distances between distributions.
|
[link]
* They suggest a slightly altered algorithm for GANs.
* The new algorithm is more stable than previous ones.
### How
* Each GAN contains a Generator that generates (fake-)examples and a Discriminator that discriminates between fake and real examples.
* Both fake and real examples can be interpreted as coming from a probability distribution.
* The basis of each GAN algorithm is to somehow measure the difference between these probability distributions
and change the network parameters of G so that the fake-distribution becomes more and more similar to the real distribution.
* There are multiple distance measures to do that:
* Total Variation (TV)
* KL-Divergence (KL)
* Jensen-Shannon divergence (JS)
* This one is based on the KL-Divergence and is the basis of the original GAN, as well as LAPGAN and DCGAN.
* Earth-Mover distance (EM), aka Wasserstein-1
* Intuitively, one can imagine both probability distributions as hilly surfaces. EM then reflects, how much mass has to be moved to convert the fake distribution to the real one.
* Ideally, a distance measure has everywhere nice values and gradients
(e.g. no +/- infinity values; no binary 0 or 1 gradients; gradients that get continously smaller when the generator produces good outputs).
* In that regard, EM beats JS and JS beats TV and KL (roughly speaking). So they use EM.
* EM
* EM is defined as
* 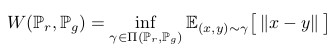
* (inf = infinum, more or less a minimum)
* which is intractable, but following the Kantorovich-Rubinstein duality it can also be calculated via
* 
* (sup = supremum, more or less a maximum)
* However, the second formula is here only valid if the network is a K-Lipschitz function (under every set of parameters).
* This can be guaranteed by simply clipping the discriminator's weights to the range `[-0.01, 0.01]`.
* Then in practice the following version of the tractable EM is used, where `w` are the parameters of the discriminator:
* 
* The full algorithm is mostly the same as for DCGAN:
* 
* Line 2 leads to training the discriminator multiple times per batch (i.e. more often than the generator).
* This is similar to the `max w in W` in the third formula (above).
* This was already part of the original GAN algorithm, but is here more actively used.
* Because of the EM distance, even a "perfect" discriminator still gives good gradient (in contrast to e.g. JS, where the discriminator should not be too far ahead). So the discriminator can be safely trained more often than the generator.
* Line 5 and 10 are derived from EM. Note that there is no more Sigmoid at the end of the discriminator!
* Line 7 is derived from the K-Lipschitz requirement (clipping of weights).
* High learning rates or using momentum-based optimizers (e.g. Adam) made the training unstable, which is why they use a small learning rate with RMSprop.
### Results
* Improved stability. The method converges to decent images with models which failed completely when using JS-divergence (like in DCGAN).
* For example, WGAN worked with generators that did not have batch normalization or only consisted of fully connected layers.
* Apparently no more mode collapse. (Mode collapse in GANs = the generator starts to generate often/always the practically same image, independent of the noise input.)
* There is a relationship between loss and image quality. Lower loss (at the generator) indicates higher image quality. Such a relationship did not exist for JS divergence.
* Example images:
* 
 |
YOLO9000: Better, Faster, Stronger
Joseph Redmon and Ali Farhadi
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/12/25 (7 years ago)
Abstract: We introduce YOLO9000, a state-of-the-art, real-time object detection system that can detect over 9000 object categories. First we propose various improvements to the YOLO detection method, both novel and drawn from prior work. The improved model, YOLOv2, is state-of-the-art on standard detection tasks like PASCAL VOC and COCO. At 67 FPS, YOLOv2 gets 76.8 mAP on VOC 2007. At 40 FPS, YOLOv2 gets 78.6 mAP, outperforming state-of-the-art methods like Faster RCNN with ResNet and SSD while still running significantly faster. Finally we propose a method to jointly train on object detection and classification. Using this method we train YOLO9000 simultaneously on the COCO detection dataset and the ImageNet classification dataset. Our joint training allows YOLO9000 to predict detections for object classes that don't have labelled detection data. We validate our approach on the ImageNet detection task. YOLO9000 gets 19.7 mAP on the ImageNet detection validation set despite only having detection data for 44 of the 200 classes. On the 156 classes not in COCO, YOLO9000 gets 16.0 mAP. But YOLO can detect more than just 200 classes; it predicts detections for more than 9000 different object categories. And it still runs in real-time.
more
less
Joseph Redmon and Ali Farhadi
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/12/25 (7 years ago)
Abstract: We introduce YOLO9000, a state-of-the-art, real-time object detection system that can detect over 9000 object categories. First we propose various improvements to the YOLO detection method, both novel and drawn from prior work. The improved model, YOLOv2, is state-of-the-art on standard detection tasks like PASCAL VOC and COCO. At 67 FPS, YOLOv2 gets 76.8 mAP on VOC 2007. At 40 FPS, YOLOv2 gets 78.6 mAP, outperforming state-of-the-art methods like Faster RCNN with ResNet and SSD while still running significantly faster. Finally we propose a method to jointly train on object detection and classification. Using this method we train YOLO9000 simultaneously on the COCO detection dataset and the ImageNet classification dataset. Our joint training allows YOLO9000 to predict detections for object classes that don't have labelled detection data. We validate our approach on the ImageNet detection task. YOLO9000 gets 19.7 mAP on the ImageNet detection validation set despite only having detection data for 44 of the 200 classes. On the 156 classes not in COCO, YOLO9000 gets 16.0 mAP. But YOLO can detect more than just 200 classes; it predicts detections for more than 9000 different object categories. And it still runs in real-time.
|
[link]
* They suggest a new version of YOLO, a model to detect bounding boxes in images.
* Their new version is more accurate, faster and is trained to recognize up to 9000 classes.
### How
* Their base model is the previous YOLOv1, which they improve here.
* Accuracy improvements
* They add batch normalization to the network.
* Pretraining usually happens on ImageNet at 224x224, fine tuning for bounding box detection then on another dataset, say Pascal VOC 2012, at higher resolutions, e.g. 448x448 in the case of YOLOv1.
This is problematic, because the pretrained network has to learn to deal with higher resolutions and a new task at the same time.
They instead first pretrain on low resolution ImageNet examples, then on higher resolution ImegeNet examples and only then switch to bounding box detection.
That improves their accuracy by about 4 percentage points mAP.
* They switch to anchor boxes, similar to Faster R-CNN. That's largely the same as in YOLOv1. Classification is now done per tested anchor box shape, instead of per grid cell.
The regression of x/y-coordinates is now a bit smarter and uses sigmoids to only translate a box within a grid cell.
* In Faster R-CNN the anchor box shapes are manually chosen (e.g. small squared boxes, large squared boxes, thin but high boxes, ...).
Here instead they learn these shapes from data.
That is done by applying k-Means to the bounding boxes in a dataset.
They cluster them into k=5 clusters and then use the centroids as anchor box shapes.
Their accuracy this way is the same as with 9 manually chosen anchor boxes.
(Using k=9 further increases their accuracy significantly, but also increases model complexity. As they want to predict 9000 classes they stay with k=5.)
* To better predict small bounding boxes, they add a pass-through connection from a higher resolution layer to the end of the network.
* They train their network now at multiple scales. (As the network is now fully convolutional, they can easily do that.)
* Speed improvements
* They get rid of their fully connected layers. Instead the network is now fully convolutional.
* They have also removed a handful or so of their convolutional layers.
* Capability improvement (weakly supervised learning)
* They suggest a method to predict bounding boxes of the 9000 most common classes in ImageNet.
They add a few more abstract classes to that (e.g. dog for all breeds of dogs) and arrive at over 9000 classes (9418 to be precise).
* They train on ImageNet and MSCOCO.
* ImageNet only contains class labels, no bounding boxes. MSCOCO only contains general classes (e.g. "dog" instead of the specific breed).
* They train iteratively on both datasets. MSCOCO is used for detection and classification, while ImageNet is only used for classification.
For an ImageNet example of class `c`, they search among the predicted bounding boxes for the one that has highest predicted probability of being `c`
and backpropagate only the classification loss for that box.
* In order to compensate the problem of different abstraction levels on the classes (e.g. "dog" vs a specific breed), they make use of WordNet.
Based on that data they generate a hierarchy/tree of classes, e.g. one path through that tree could be: object -> animal -> canine -> dog -> hunting dog -> terrier -> yorkshire terrier.
They let the network predict paths in that hierarchy, so that the prediction "dog" for a specific dog breed is not completely wrong.
* Visualization of the hierarchy:
* 
* They predict many small softmaxes for the paths in the hierarchy, one per node:
* 
### Results
* Accuracy
* They reach about 73.4 mAP when training on Pascal VOC 2007 and 2012. That's slightly behind Faster R-CNN with VGG16 with 75.9 mAP, trained on MSCOCO+2007+2012.
* Speed
* They reach 91 fps (10ms/image) at image resolution 288x288 and 40 fps (25ms/image) at 544x544.
* Weakly supervised learning
* They test their 9000-class-detection on ImageNet's detection task, which contains bounding boxes for 200 object classes.
* They achieve 19.7 mAP for all classes and 16.0% mAP for the 156 classes which are not part of MSCOCO.
* For some classes they get 0 mAP accuracy.
* The system performs well for all kinds of animals, but struggles with not-living objects, like sunglasses.
* Example images (notice the class labels):
* 
 |
You Only Look Once: Unified, Real-Time Object Detection
Redmon, Joseph and Divvala, Santosh Kumar and Girshick, Ross B. and Farhadi, Ali
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
Redmon, Joseph and Divvala, Santosh Kumar and Girshick, Ross B. and Farhadi, Ali
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a model ("YOLO") to detect bounding boxes in images.
* In comparison to Faster R-CNN, this model is faster but less accurate.
### How
* Architecture
* Input are images with a resolution of 448x448.
* Output are `S*S*(B*5 + C)` values (per image).
* `S` is the grid size (default value: 7). Each image is split up into `S*S` cells.
* `B` is the number of "tested" bounding box shapes at each cell (default value: 2).
So at each cell, the network might try one large and one small bounding box.
The network predicts additionally for each such tested bounding box `5` values.
These cover the exact position (x, y) and scale (height, width) of the bounding box as well as a confidence value.
They allow the network to fine tune the bounding box shape and reject it, e.g. if there is no object in the grid cell.
The confidence value is zero if there is no object in the grid cell and otherwise matches the IoU between predicted and true bounding box.
* `C` is the number of classes in the dataset (e.g. 20 in Pascal VOC). For each grid cell, the model decides once to which of the `C` objects the cell belongs.
* Rough overview of their outputs:
* 
* In contrast to Faster R-CNN, their model does *not* use a separate region proposal network (RPN).
* Per bounding box they actually predict the *square root* of height and width instead of the raw values.
That is supposed to result in similar errors/losses for small and big bounding boxes.
* They use a total of 24 convolutional layers and 2 fully connected layers.
* Some of these convolutional layers are 1x1-convs that halve the number of channels (followed by 3x3s that double them again).
* Overview of the architecture:
* 
* They use Leaky ReLUs (alpha=0.1) throughout the network. The last layer uses linear activations (apparently even for the class prediction...!?).
* Similarly to Faster R-CNN, they use a non maximum suppression that drops predicted bounding boxes if they are too similar to other predictions.
* Training
* They pretrain their network on ImageNet, then finetune on Pascal VOC.
* Loss
* They use sum-squared losses (apparently even for the classification, i.e. the `C` values).
* They dont propagate classification loss (for `C`) for grid cells that don't contain an object.
* For each grid grid cell they "test" `B` example shapes of bounding boxes (see above).
Among these `B` shapes, they only propagate the bounding box losses (regarding x, y, width, height, confidence) for the shape that has highest IoU with a ground truth bounding box.
* Most grid cells don't contain a bounding box. Their confidence values will all be zero, potentialle dominating the total loss.
To prevent that, the weighting of the confidence values in the loss function is reduced relative to the regression components (x, y, height, width).
### Results
* The coarse grid and B=2 setting lead to some problems. Namely, small objects are missed and bounding boxes can end up being dropped if they are too close to other bounding boxes.
* The model also has problems with unusual bounding box shapes.
* Overall their accuracy is about 10 percentage points lower than Faster R-CNN with VGG16 (63.4% vs 73.2%, measured in mAP on Pascal VOC 2007).
* They achieve 45fps (22ms/image), compared to 7fps (142ms/image) with Faster R-CNN + VGG16.
* Overview of results on Pascal VOC 2012:
* 
* They also suggest a faster variation of their model which reached 145fps (7ms/image) at a further drop of 10 percentage points mAP (to 52.7%).
* A significant part of their error seems to come from badly placed or sized bounding boxes (e.g. too wide or too much to the right).
* They mistake background less often for objects than Fast R-CNN. They test combining both models with each other and can improve Fast R-CNN's accuracy by about 2.5 percentage points mAP.
* They test their model on paintings/artwork (Picasso and People-Art datasets) and notice that it generalizes fairly well to that domain.
* Example results (notice the paintings at the top):
* 
 |
PVANet: Lightweight Deep Neural Networks for Real-time Object Detection
Sanghoon Hong and Byungseok Roh and Kye-Hyeon Kim and Yeongjae Cheon and Minje Park
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/11/23 (7 years ago)
Abstract: In object detection, reducing computational cost is as important as improving accuracy for most practical usages. This paper proposes a novel network structure, which is an order of magnitude lighter than other state-of-the-art networks while maintaining the accuracy. Based on the basic principle of more layers with less channels, this new deep neural network minimizes its redundancy by adopting recent innovations including C.ReLU and Inception structure. We also show that this network can be trained efficiently to achieve solid results on well-known object detection benchmarks: 84.9% and 84.2% mAP on VOC2007 and VOC2012 while the required compute is less than 10% of the recent ResNet-101.
more
less
Sanghoon Hong and Byungseok Roh and Kye-Hyeon Kim and Yeongjae Cheon and Minje Park
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/11/23 (7 years ago)
Abstract: In object detection, reducing computational cost is as important as improving accuracy for most practical usages. This paper proposes a novel network structure, which is an order of magnitude lighter than other state-of-the-art networks while maintaining the accuracy. Based on the basic principle of more layers with less channels, this new deep neural network minimizes its redundancy by adopting recent innovations including C.ReLU and Inception structure. We also show that this network can be trained efficiently to achieve solid results on well-known object detection benchmarks: 84.9% and 84.2% mAP on VOC2007 and VOC2012 while the required compute is less than 10% of the recent ResNet-101.
|
[link]
* They present a variation of Faster R-CNN.
* Faster R-CNN is a model that detects bounding boxes in images.
* Their variation is about as accurate as the best performing versions of Faster R-CNN.
* Their variation is significantly faster than these variations (roughly 50ms per image).
### How
* PVANET reuses the standard Faster R-CNN architecture:
* A base network that transforms an image into a feature map.
* A region proposal network (RPN) that uses the feature map to predict bounding box candidates.
* A classifier that uses the feature map and the bounding box candidates to predict the final bounding boxes.
* PVANET modifies the base network and keeps the RPN and classifier the same.
* Inception
* Their base network uses eight Inception modules.
* They argue that these are good choices here, because they are able to represent an image at different scales (aka at different receptive field sizes)
due to their mixture of 3x3 and 1x1 convolutions.
* 
* Representing an image at different scales is useful here in order to detect both large and small bounding boxes.
* Inception modules are also reasonably fast.
* Visualization of their Inception modules:
* 
* Concatenated ReLUs
* Before the eight Inception modules, they start the network with eight convolutions using concatenated ReLUs.
* These CReLUs compute both the classic ReLU result (`max(0, x)`) and concatenate to that the negated result, i.e. something like `f(x) = max(0, x <concat> (-1)*x)`.
* That is done, because among the early one can often find pairs of convolution filters that are the negated variations of each other.
So by adding CReLUs, the network does not have to compute these any more, instead they are created (almost) for free, reducing the computation time by up to 50%.
* Visualization of their final CReLU block:
* TODO
* 
* Multi-Scale output
* Usually one would generate the final feature map simply from the output of the last convolution.
* They instead combine the outputs of three different convolutions, each resembling a different scale (or level of abstraction).
* They take one from an early point of the network (downscaled), one from the middle part (kept the same) and one from the end (upscaled).
* They concatenate these and apply a 1x1 convolution to generate the final output.
* Other stuff
* Most of their network uses residual connections (including the Inception modules) to facilitate learning.
* They pretrain on ILSVRC2012 and then perform fine-tuning on MSCOCO, VOC 2007 and VOC 2012.
* They use plateau detection for their learning rate, i.e. if a moving average of the loss does not improve any more, they decrease the learning rate. They say that this increases accuracy significantly.
* The classifier in Faster R-CNN consists of fully connected layers. They compress these via Truncated SVD to speed things up. (That was already part of Fast R-CNN, I think.)
### Results
* On Pascal VOC 2012 they achieve 82.5% mAP at 46ms/image (Titan X GPU).
* Faster R-CNN + ResNet-101: 83.8% at 2.2s/image.
* Faster R-CNN + VGG16: 75.9% at 110ms/image.
* R-FCN + ResNet-101: 82.0% at 133ms/image.
* Decreasing the number of region proposals from 300 per image to 50 almost doubles the speed (to 27ms/image) at a small loss of 1.5 percentage points mAP.
* Using Truncated SVD for the classifier reduces the required timer per image by about 30% at roughly 1 percentage point of mAP loss.
 |
R-FCN: Object Detection via Region-based Fully Convolutional Networks
Dai, Jifeng and Li, Yi and He, Kaiming and Sun, Jian
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
Dai, Jifeng and Li, Yi and He, Kaiming and Sun, Jian
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They present a variation of Faster R-CNN, i.e. a model that predicts bounding boxes in images and classifies them.
* In contrast to Faster R-CNN, their model is fully convolutional.
* In contrast to Faster R-CNN, the computation per bounding box candidate (region proposal) is very low.
### How
* The basic architecture is the same as in Faster R-CNN:
* A base network transforms an image to a feature map. Here they use ResNet-101 to do that.
* A region proposal network (RPN) uses the feature map to locate bounding box candidates ("region proposals") in the image.
* A classifier uses the feature map and the bounding box candidates and classifies each one of them into `C+1` classes,
where `C` is the number of object classes to spot (e.g. "person", "chair", "bottle", ...) and `1` is added for the background.
* During that process, small subregions of the feature maps (those that match the bounding box candidates) must be extracted and converted to fixed-sizes matrices.
The method to do that is called "Region of Interest Pooling" (RoI-Pooling) and is based on max pooling.
It is mostly the same as in Faster R-CNN.
* Visualization of the basic architecture:
* 
* Position-sensitive classification
* Fully convolutional bounding box detectors tend to not work well.
* The authors argue, that the problems come from the translation-invariance of convolutions, which is a desirable property in the case of classification but not when precise localization of objects is required.
* They tackle that problem by generating multiple heatmaps per object class, each one being slightly shifted ("position-sensitive score maps").
* More precisely:
* The classifier generates per object class `c` a total of `k*k` heatmaps.
* In the simplest form `k` is equal to `1`. Then only one heatmap is generated, which signals whether a pixel is part of an object of class `c`.
* They use `k=3*3`. The first of those heatmaps signals, whether a pixel is part of the *top left* corner of a bounding box of class `c`. The second heatmap signals, whether a pixel is part of the *top center* of a bounding box of class `c` (and so on).
* The RoI-Pooling is applied to these heatmaps.
* For `k=3*3`, each bounding box candidate is converted to `3*3` values. The first one resembles the top left corner of the bounding box candidate. Its value is generated by taking the average of the values in that area in the first heatmap.
* Once the `3*3` values are generated, the final score of class `c` for that bounding box candidate is computed by averaging the values.
* That process is repeated for all classes and a softmax is used to determine the final class.
* The graphic below shows examples for that:
* 
* The above described RoI-Pooling uses only averages and hence is almost (computationally) free.
* They make use of that during the training by sampling many candidates and only backpropagating on those with high losses (online hard example mining, OHEM).
* À trous trick
* In order to increase accuracy for small bounding boxes they use the à trous trick.
* That means that they use a pretrained base network (here ResNet-101), then remove a pooling layer and set the à trous rate (aka dilation) of all convolutions after the removed pooling layer to `2`.
* The á trous rate describes the distance of sampling locations of a convolution. Usually that is `1` (sampled locations are right next to each other). If it is set to `2`, there is one value "skipped" between each pair of neighbouring sampling location.
* By doing that, the convolutions still behave as if the pooling layer existed (and therefore their weights can be reused). At the same time, they work at an increased resolution, making them more capable of classifying small objects. (Runtime increases though.)
* Training of R-FCN happens similarly to Faster R-CNN.
### Results
* Similar accuracy as the most accurate Faster R-CNN configurations at a lower runtime of roughly 170ms per image.
* Switching to ResNet-50 decreases accuracy by about 2 percentage points mAP (at faster runtime). Switching to ResNet-152 seems to provide no measureable benefit.
* OHEM improves mAP by roughly 2 percentage points.
* À trous trick improves mAP by roughly 2 percentage points.
* Training on `k=1` (one heatmap per class) results in a failure, i.e. a model that fails to predict bounding boxes. `k=7` is slightly more accurate than `k=3`.

1 Comments
|
Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks
Ren, Shaoqing and He, Kaiming and Girshick, Ross B. and Sun, Jian
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
Ren, Shaoqing and He, Kaiming and Girshick, Ross B. and Sun, Jian
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* R-CNN and its successor Fast R-CNN both rely on a "classical" method to find region proposals in images (i.e. "Which regions of the image look like they *might* be objects?").
* That classical method is selective search.
* Selective search is quite slow (about two seconds per image) and hence the bottleneck in Fast R-CNN.
* They replace it with a neural network (region proposal network, aka RPN).
* The RPN reuses the same features used for the remainder of the Fast R-CNN network, making the region proposal step almost free (about 10ms).
### How
* They now have three components in their network:
* A model for feature extraction, called the "feature extraction network" (**FEN**). Initialized with the weights of a pretrained network (e.g. VGG16).
* A model to use these features and generate region proposals, called the "Region Proposal Network" (**RPN**).
* A model to use these features and region proposals to classify each regions proposal's object and readjust the bounding box, called the "classification network" (**CN**). Initialized with the weights of a pretrained network (e.g. VGG16).
* Usually, FEN will contain the convolutional layers of the pretrained model (e.g. VGG16), while CN will contain the fully connected layers.
* (Note: Only "RPN" really pops up in the paper, the other two remain more or less unnamed. I added the two names to simplify the description.)
* Rough architecture outline:
* 
* The basic method at test is as follows:
1. Use FEN to convert the image to features.
2. Apply RPN to the features to generate region proposals.
3. Use Region of Interest Pooling (RoI-Pooling) to convert the features of each region proposal to a fixed sized vector.
4. Apply CN to the RoI-vectors to a) predict the class of each object (out of `K` object classes and `1` background class) and b) readjust the bounding box dimensions (top left coordinate, height, width).
* RPN
* Basic idea:
* Place anchor points on the image, all with the same distance to each other (regular grid).
* Around each anchor point, extract rectangular image areas in various shapes and sizes ("anchor boxes"), e.g. thin/square/wide and small/medium/large rectangles. (More precisely: The features of these areas are extracted.)
* Visualization:
* 
* Feed the features of these areas through a classifier and let it rate/predict the "regionness" of the rectangle in a range between 0 and 1. Values greater than 0.5 mean that the classifier thinks the rectangle might be a bounding box. (CN has to analyze that further.)
* Feed the features of these areas through a regressor and let it optimize the region size (top left coordinate, height, width). That way you get all kinds of possible bounding box shapes, even though you only use a few base shapes.
* Implementation:
* The regular grid of anchor points naturally arises due to the downscaling of the FEN, it doesn't have to be implemented explicitly.
* The extraction of anchor boxes and classification + regression can be efficiently implemented using convolutions.
* They first apply a 3x3 convolution on the feature maps. Note that the convolution covers a large image area due to the downscaling.
* Not so clear, but sounds like they use 256 filters/kernels for that convolution.
* Then they apply some 1x1 convolutions for the classification and regression.
* They use `2*k` 1x1 convolutions for classification and `4*k` 1x1 convolutions for regression, where `k` is the number of different shapes of anchor boxes.
* They use `k=9` anchor box types: Three sizes (small, medium, large), each in three shapes (thin, square, wide).
* The way they build training examples (below) forces some 1x1 convolutions to react only to some anchor box types.
* Training:
* Positive examples are anchor boxes that have an IoU with a ground truth bounding box of 0.7 or more. If no anchor point has such an IoU with a specific box, the one with the highest IoU is used instead.
* Negative examples are all anchor boxes that have IoU that do not exceed 0.3 for any bounding box.
* Any anchor point that falls in neither of these groups does not contribute to the loss.
* Anchor boxes that would violate image boundaries are not used as examples.
* The loss is similar to the one in Fast R-CNN: A sum consisting of log loss for the classifier and smooth L1 loss (=smoother absolute distance) for regression.
* Per batch they only sample examples from one image (for efficiency).
* They use 128 positive examples and 128 negative ones. If they can't come up with 128 positive examples, they add more negative ones.
* Test:
* They use non-maximum suppression (NMS) to remove too identical region proposals, i.e. among all region proposals that have an IoU overlap of 0.7 or more, they pick the one that has highest score.
* They use the 300 proposals with highest score after NMS (or less if there aren't that many).
* Feature sharing
* They want to share the features of the FEN between the RPN and the CN.
* So they need a special training method that fine-tunes all three components while keeping the features extracted by FEN useful for both RPN and CN at the same time (not only for one of them).
* Their training methods are:
* Alternating traing: One batch for FEN+RPN, one batch for FEN+CN, then again one batch for FEN+RPN and so on.
* Approximate joint training: Train one network of FEN+RPN+CN. Merge the gradients of RPN and CN that arrive at FEN via simple summation. This method does not compute a gradient from CN through the RPN's regression task, as that is non-trivial. (This runs 25-50% faster than alternating training, accuracy is mostly the same.)
* Non-approximate joint training: This would compute the above mentioned missing gradient, but isn't implemented.
* 4-step alternating training:
1. Clone FEN to FEN1 and FEN2.
2. Train the pair FEN1 + RPN.
3. Train the pair FEN2 + CN using the region proposals from the trained RPN.
4. Fine-tune the pair FEN2 + RPN. FEN2 is fixed, RPN takes the weights from step 2.
5. Fine-tune the pair FEN2 + CN. FEN2 is fixed, CN takes the weights from step 3, region proposals come from RPN from step 4.
* Results
* Example images:
* 
* Pascal VOC (with VGG16 as FEN)
* Using an RPN instead of SS (selective search) slightly improved mAP from 66.9% to 69.9%.
* Training RPN and CN on the same FEN (sharing FEN's weights) does not worsen the mAP, but instead improves it slightly from 68.5% to 69.9%.
* Using the RPN instead of SS significantly speeds up the network, from 1830ms/image (less than 0.5fps) to 198ms/image (5fps). (Both stats with VGG16. They also use ZF as the FEN, which puts them at 17fps, but mAP is lower.)
* Using per anchor point more scales and shapes (ratios) for the anchor boxes improves results.
* 1 scale, 1 ratio: 65.8% mAP (scale `128*128`, ratio 1:1) or 66.7% mAP (scale `256*256`, same ratio).
* 3 scales, 3 ratios: 69.9% mAP (scales `128*128`, `256*256`, `512*512`; ratios 1:1, 1:2, 2:1).
* Two-staged vs one-staged
* Instead of the two-stage system (first, generate proposals via RPN, then classify them via CN), they try a one-staged system.
* In the one-staged system they move a sliding window over the computed feature maps and regress at every location the bounding box sizes and classify the box.
* When doing this, their performance drops from 58.7% to about 54%.
 |
Fast R-CNN
Girshick, Ross B.
International Conference on Computer Vision - 2015 via Local Bibsonomy
Keywords: dblp
Girshick, Ross B.
International Conference on Computer Vision - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* The original R-CNN had three major disadvantages:
1. Two-staged training pipeline: Instead of only training a CNN, one had to train first a CNN and then multiple SVMs.
2. Expensive training: Training was slow and required lots of disk space (feature vectors needed to be written to disk for all region proposals (2000 per image) before training the SVMs).
3. Slow test: Each region proposal had to be handled independently.
* Fast R-CNN ist an improved version of R-CNN and tackles the mentioned problems.
* It no longer uses SVMs, only CNNs (single-stage).
* It does one single feature extraction per image instead of per region, making it much faster (9x faster at training, 213x faster at test).
* It is more accurate than R-CNN.
### How
* The basic architecture, training and testing methods are mostly copied from R-CNN.
* For each image at test time they do:
* They generate region proposals via selective search.
* They feed the image once through the convolutional layers of a pre-trained network, usually VGG16.
* For each region proposal they extract the respective region from the features generated by the network.
* The regions can have different sizes, but the following steps need fixed size vectors. So each region is downscaled via max-pooling so that it has a size of 7x7 (so apparently they ignore regions of sizes below 7x7...?).
* This is called Region of Interest Pooling (RoI-Pooling).
* During the backwards pass, partial derivatives can be transferred to the maximum value (as usually in max pooling). That derivative values are summed up over different regions (in the same image).
* They reshape the 7x7 regions to vectors of length `F*7*7`, where `F` was the number of filters in the last convolutional layer.
* They feed these vectors through another network which predicts:
1. The class of the region (including background class).
2. Top left x-coordinate, top left y-coordinate, log height and log width of the bounding box (i.e. it fine-tunes the region proposal's bounding box). These values are predicted once for every class (so `K*4` values).
* Architecture as image:
* 
* Sampling for training
* Efficiency
* If batch size is `B` it is inefficient to sample regions proposals from `B` images as each image will require a full forward pass through the base network (e.g. VGG16).
* It is much more efficient to use few images to share most of the computation between region proposals.
* They use two images per batch (each 64 region proposals) during training.
* This technique introduces correlations between examples in batches, but they did not observe any problems from that.
* They call this technique "hierarchical sampling" (first images, then region proposals).
* IoUs
* Positive examples for specific classes during training are region proposals that have an IoU with ground truth bounding boxes of `>=0.5`.
* Examples for background region proposals during training have IoUs with any ground truth box in the interval `(0.1, 0.5]`.
* Not picking IoUs below 0.1 is similar to hard negative mining.
* They use 25% positive examples, 75% negative/background examples per batch.
* They apply horizontal flipping as data augmentation, nothing else.
* Outputs
* For their class predictions the use a simple softmax with negative log likelihood.
* For their bounding box regression they use a smooth L1 loss (similar to mean absolute error, but switches to mean squared error for very low values).
* Smooth L1 loss is less sensitive to outliers and less likely to suffer from exploding gradients.
* The smooth L1 loss is only active for positive examples (not background examples). (Not active means that it is zero.)
* Training schedule
* The use SGD.
* They train 30k batches with learning rate 0.001, then 0.0001 for another 10k batches. (On Pascal VOC, they use more batches on larger datasets.)
* They use twice the learning rate for the biases.
* They use momentum of 0.9.
* They use parameter decay of 0.0005.
* Truncated SVD
* The final network for class prediction and bounding box regression has to be applied to every region proposal.
* It contains one large fully connected hidden layer and one fully connected output layer (`K+1` classes plus `K*4` regression values).
* For 2000 proposals that becomes slow.
* So they compress the layers after training to less weights via truncated SVD.
* A weights matrix is approximated via 
* U (`u x t`) are the first `t` left-singular vectors of W.
* Sigma is a `t x t` diagonal matrix of the top `t` singular values.
* V (`v x t`) are the first `t` right-singular vectors of W.
* W is then replaced by two layers: One contains `Sigma V^T` as weights (no biases), the other contains `U` as weights (with original biases).
* Parameter count goes down to `t(u+v)` from `uv`.
### Results
* They try three base models:
* AlexNet (Small, S)
* VGG-CNN-M-1024 (Medium, M)
* VGG16 (Large, L)
* On VGG16 and Pascal VOC 2007, compared to original R-CNN:
* Training time down to 9.5h from 84h (8.8x faster).
* Test rate *with SVD* (1024 singular values) improves from 47 seconds per image to 0.22 seconds per image (213x faster).
* Test rate *without SVD* improves similarly to 0.32 seconds per image.
* mAP improves from 66.0% to 66.6% (66.9% without SVD).
* Per class accuracy results:
* Fast_R-CNN__pvoc2012.jpg
* 
* Fixing the weights of VGG16's convolutional layers and only fine-tuning the fully connected layers (those are applied to each region proposal), decreases the accuracy to 61.4%.
* This decrease in accuracy is most significant for the later convolutional layers, but marginal for the first layers.
* Therefor they only train the convolutional layers starting with `conv3_1` (9 out of 13 layers), which speeds up training.
* Multi-task training
* Training models on classification and bounding box regression instead of only on classification improves the mAP (from 62.6% to 66.9%).
* Doing this in one hierarchy instead of two seperate models (one for classification, one for bounding box regression) increases mAP by roughly 2-3 percentage points.
* They did not find a significant benefit of training the model on multiple scales (e.g. same image sometimes at 400x400, sometimes at 600x600, sometimes at 800x800 etc.).
* Note that their raw CNN (everything before RoI-Pooling) is fully convolutional, so they can feed the images at any scale through the network.
* Increasing the amount of training data seemed to improve mAP a bit, but not as much as one might hope for.
* Using a softmax loss instead of an SVM seemed to marginally increase mAP (0-1 percentage points).
* Using more region proposals from selective search does not simply increase mAP. Instead it can lead to higher recall, but lower precision.
* 
* Using densely sampled region proposals (as in sliding window) significantly reduces mAP (from 59.2% to 52.9%). If SVMs instead of softmaxes are used, the results are even worse (49.3%).
 |
Rich Feature Hierarchies for Accurate Object Detection and Semantic Segmentation
Girshick, Ross B. and Donahue, Jeff and Darrell, Trevor and Malik, Jitendra
Conference and Computer Vision and Pattern Recognition - 2014 via Local Bibsonomy
Keywords: dblp
Girshick, Ross B. and Donahue, Jeff and Darrell, Trevor and Malik, Jitendra
Conference and Computer Vision and Pattern Recognition - 2014 via Local Bibsonomy
Keywords: dblp
|
[link]
* Previously, methods to detect bounding boxes in images were often based on the combination of manual feature extraction with SVMs.
* They replace the manual feature extraction with a CNN, leading to significantly higher accuracy.
* They use supervised pre-training on auxiliary datasets to deal with the small amount of labeled data (instead of the sometimes used unsupervised pre-training).
* They call their method R-CNN ("Regions with CNN features").
### How
* Their system has three modules: 1) Region proposal generation, 2) CNN-based feature extraction per region proposal, 3) classification.
* 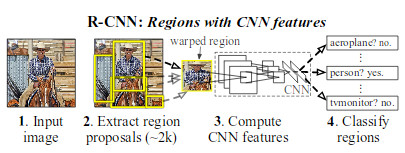
* Region proposals generation
* A region proposal is a bounding box candidate that *might* contain an object.
* By default they generate 2000 region proposals per image.
* They suggest "simple" (i.e. not learned) algorithms for this step (e.g. objectneess, selective search, CPMC).
* They use selective search (makes it comparable to previous systems).
* CNN features
* Uses a CNN to extract features, applied to each region proposal (replaces the previously used manual feature extraction).
* So each region proposal ist turned into a fixed length vector.
* They use AlexNet by Krizhevsky et al. as their base CNN (takes 227x227 RGB images, converts them into 4096-dimensional vectors).
* They add `p=16` pixels to each side of every region proposal, extract the pixels and then simply resize them to 227x227 (ignoring aspect ratio, so images might end up distorted).
* They generate one 4096d vector per image, which is less than what some previous manual feature extraction methods used. That enables faster classification, less memory usage and thus more possible classes.
* Classification
* A classifier that receives the extracted feature vectors (one per region proposal) and classifies them into a predefined set of available classes (e.g. "person", "car", "bike", "background / no object").
* They use one SVM per available class.
* The regions that were not classified as background might overlap (multiple bounding boxes on the same object).
* They use greedy non-maximum suppresion to fix that problem (for each class individually).
* That method simply rejects regions if they overlap strongly with another region that has higher score.
* Overlap is determined via Intersection of Union (IoU).
* Training method
* Pre-Training of CNN
* They use AlexNet pretrained on Imagenet (1000 classes).
* They replace the last fully connected layer with a randomly initialized one that leads to `C+1` classes (`C` object classes, `+1` for background).
* Fine-Tuning of CNN
* The use SGD with learning rate `0.001`.
* Batch size is 128 (32 positive windows, 96 background windows).
* A region proposal is considered positive, if its IoU with any ground-truth bounding box is `>=0.5`.
* SVM
* They train one SVM per class via hard negative mining.
* For positive examples they use here an IoU threshold of `>=0.3`, which performed better than 0.5.
### Results
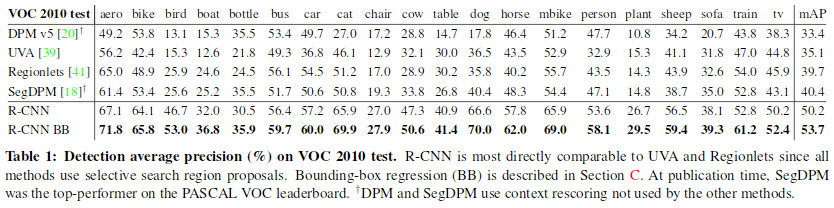
* Pascal VOC 2010
* They: 53.7% mAP
* Closest competitor (SegDPM): 40.4% mAP
* Closest competitor that uses the same region proposal method (UVA): 35.1% mAP
* 
* ILSVRC2013 detection
* They: 31.4% mAP
* Closest competitor (OverFeat): 24.3% mAP
* The feed a large number of region proposals through the network and log for each filter in the last conv-layer which images activated it the most:
* 
* Usefulness of layers:
* They remove later layers of the network and retrain in order to find out which layers are the most useful ones.
* Their result is that both fully connected layers of AlexNet seemed to be very domain-specific and profit most from fine-tuning.
* Using VGG16:
* Using VGG16 instead of AlexNet increased mAP from 58.5% to 66.0% on Pascal VOC 2007.
* Computation time was 7 times higher.
* They train a linear regression model that improves the bounding box dimensions based on the extracted features of the last pooling layer. That improved their mAP by 3-4 percentage points.
* The region proposals generated by selective search have a recall of 98% on Pascal VOC and 91.6% on ILSVRC2013 (measured by IoU of `>=0.5`).
 |
Ten Years of Pedestrian Detection, What Have We Learned?
Benenson, Rodrigo and Omran, Mohamed and Hosang, Jan Hendrik and Schiele, Bernt
European Conference on Computer Vision - 2014 via Local Bibsonomy
Keywords: dblp
Benenson, Rodrigo and Omran, Mohamed and Hosang, Jan Hendrik and Schiele, Bernt
European Conference on Computer Vision - 2014 via Local Bibsonomy
Keywords: dblp
|
[link]
* They compare the results of various models for pedestrian detection.
* The various models were developed over the course of ~10 years (2003-2014).
* They analyze which factors seemed to improve the results.
* They derive new models for pedestrian detection from that.
### Comparison: Datasets
* Available datasets
* INRIA: Small dataset. Diverse images.
* ETH: Video dataset. Stereo images.
* TUD-Brussels: Video dataset.
* Daimler: No color channel.
* Daimler stereo: Stereo images.
* Caltech-USA: Most often used. Large dataset.
* KITTI: Often used. Large dataset. Stereo images.
* All datasets except KITTI are part of the "unified evaluation toolbox" that allows authors to easily test on all of these datasets.
* The evaluation started initially with per-window (FPPW) and later changed to per-image (FPPI), because per-window skewed the results.
* Common evaluation metrics:
* MR: Log-average miss-rate (lower is better)
* AUC: Area under the precision-recall curve (higher is better)
### Comparison: Methods
* Families
* They identified three families of methods: Deformable Parts Models, Deep Neural Networks, Decision Forests.
* Decision Forests was the most popular family.
* No specific family seemed to perform better than other families.
* There was no evidence that non-linearity in kernels was needed (given sophisticated features).
* Additional data
* Adding (coarse) optical flow data to each image seemed to consistently improve results.
* There was some indication that adding stereo data to each image improves the results.
* Context
* For sliding window detectors, adding context from around the window seemed to improve the results.
* E.g. context can indicate whether there were detections next to the window as people tend to walk in groups.
* Deformable parts
* They saw no evidence that deformable part models outperformed other models.
* Multi-Scale models
* Training separate models for each sliding window scale seemed to improve results slightly.
* Deep architectures
* They saw no evidence that deep neural networks outperformed other models. (Note: Paper is from 2014, might have changed already?)
* Features
* Best performance was usually achieved with simple HOG+LUV features, i.e. by converting each window into:
* 6 channels of gradient orientations
* 1 channel of gradient magnitude
* 3 channels of LUV color space
* Some models use significantly more channels for gradient orientations, but there was no evidence that this was necessary to achieve good accuracy.
* However, using more different features (and more sophisticated ones) seemed to improve results.
### Their new model:
* They choose Decisions Forests as their model framework (2048 level-2 trees, i.e. 3 thresholds per tree).
* They use features from the [Integral Channels Features framework](http://pages.ucsd.edu/~ztu/publication/dollarBMVC09ChnFtrs_0.pdf). (Basically just a mixture of common/simple features per window.)
* They add optical flow as a feature.
* They add context around the window as a feature. (A second detector that detects windows containing two persons.)
* Their model significantly improves upon the state of the art (from 34 to 22% MR on Caltech dataset).
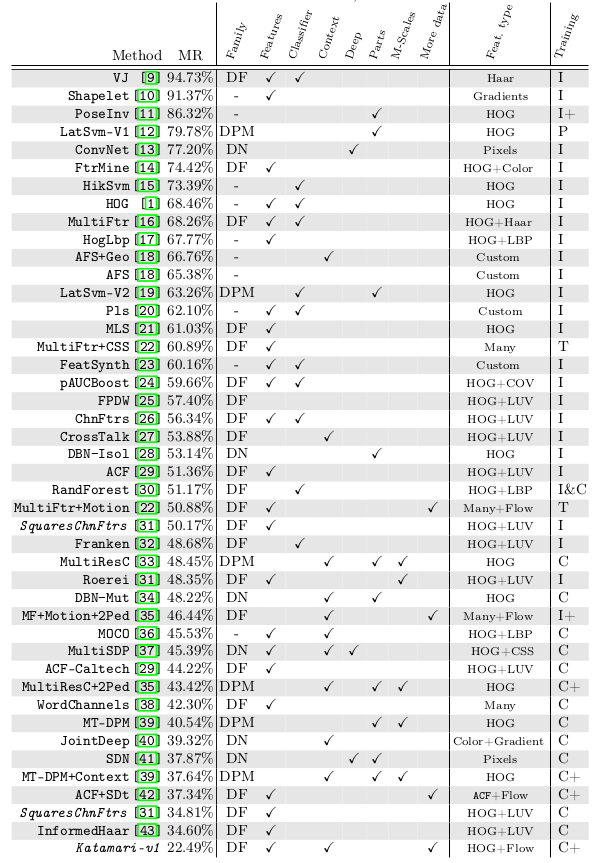
*Overview of models developed over the years, starting with Viola Jones (VJ) and ending with their suggested model (Katamari-v1). (DF = Decision Forest, DPM = Deformable Parts Model, DN = Deep Neural Network; I = Inria Dataset, C = Caltech Dataset)*
 |
Instance Normalization: The Missing Ingredient for Fast Stylization
Dmitry Ulyanov and Andrea Vedaldi and Victor Lempitsky
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/07/27 (7 years ago)
Abstract: It this paper we revisit the fast stylization method introduced in Ulyanov et. al. (2016). We show how a small change in the stylization architecture results in a significant qualitative improvement in the generated images. The change is limited to swapping batch normalization with instance normalization, and to apply the latter both at training and testing times. The resulting method can be used to train high-performance architectures for real-time image generation. The code will is made available on github.
more
less
Dmitry Ulyanov and Andrea Vedaldi and Victor Lempitsky
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/07/27 (7 years ago)
Abstract: It this paper we revisit the fast stylization method introduced in Ulyanov et. al. (2016). We show how a small change in the stylization architecture results in a significant qualitative improvement in the generated images. The change is limited to swapping batch normalization with instance normalization, and to apply the latter both at training and testing times. The resulting method can be used to train high-performance architectures for real-time image generation. The code will is made available on github.
|
[link]
* Style transfer between images works - in its original form - by iteratively making changes to a content image, so that its style matches more and more the style of a chosen style image.
* That iterative process is very slow.
* Alternatively, one can train a single feed-forward generator network to apply a style in one forward pass. The network is trained on a dataset of input images and their stylized versions (stylized versions can be generated using the iterative approach).
* So far, these generator networks were much faster than the iterative approach, but their quality was lower.
* They describe a simple change to these generator networks to increase the image quality (up to the same level as the iterative approach).
### How
* In the generator networks, they simply replace all batch normalization layers with instance normalization layers.
* Batch normalization normalizes using the information from the whole batch, while instance normalization normalizes each feature map on its own.
* Equations
* Let `H` = Height, `W` = Width, `T` = Batch size
* Batch Normalization:
* 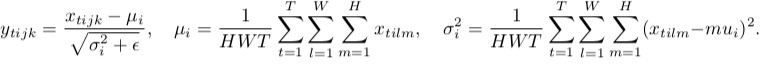
* Instance Normalization
* 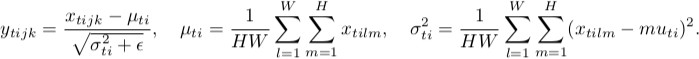
* They apply instance normalization at test time too (identically).
### Results
* Same image quality as iterative approach (at a fraction of the runtime).
* One content image with two different styles using their approach:
* 
 |
Stacked Hourglass Networks for Human Pose Estimation
Alejandro Newell and Kaiyu Yang and Jia Deng
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/03/22 (8 years ago)
Abstract: This work introduces a novel Convolutional Network architecture for the task of human pose estimation. Features are processed across all scales and consolidated to best capture the various spatial relationships associated with the body. We show how repeated bottom-up, top-down processing used in conjunction with intermediate supervision is critical to improving the performance of the network. We refer to the architecture as a 'stacked hourglass' network based on the successive steps of pooling and upsampling that are done to produce a final set of estimates. State-of-the-art results are achieved on the FLIC and MPII benchmarks outcompeting all recent methods.
more
less
Alejandro Newell and Kaiyu Yang and Jia Deng
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/03/22 (8 years ago)
Abstract: This work introduces a novel Convolutional Network architecture for the task of human pose estimation. Features are processed across all scales and consolidated to best capture the various spatial relationships associated with the body. We show how repeated bottom-up, top-down processing used in conjunction with intermediate supervision is critical to improving the performance of the network. We refer to the architecture as a 'stacked hourglass' network based on the successive steps of pooling and upsampling that are done to produce a final set of estimates. State-of-the-art results are achieved on the FLIC and MPII benchmarks outcompeting all recent methods.
|
[link]
Official code: https://github.com/anewell/pose-hg-train
* They suggest a new model architecture for human pose estimation (i.e. "lay a skeleton over a person").
* Their architecture is based progressive pooling followed by progressive upsampling, creating an hourglass form.
* Input are images showing a person's body.
* Outputs are K heatmaps (for K body joints), with each heatmap showing the likely position of a single joint on the person (e.g. "akle", "wrist", "left hand", ...).
### How
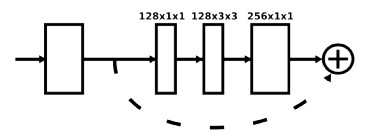
* *Basic building block*
* They use residuals as their basic building block.
* Each residual has three layers: One 1x1 convolution for dimensionality reduction (from 256 to 128 channels), a 3x3 convolution, a 1x1 convolution for dimensionality increase (back to 256).
* Visualized:
* 
* *Architecture*
* Their architecture starts with one standard 7x7 convolutions that has strides of (2, 2).
* They use MaxPooling (2x2, strides of (2, 2)) to downsample the images/feature maps.
* They use Nearest Neighbour upsampling (factor 2) to upsample the images/feature maps.
* After every pooling step they add three of their basic building blocks.
* Before each pooling step they branch off the current feature map as a minor branch and apply three basic building blocks to it. Then they add it back to the main branch after that one has been upsampeled again to the original size.
* The feature maps between each basic building block have (usually) 256 channels.
* Their HourGlass ends in two 1x1 convolutions that create the heatmaps.
* They stack two of their HourGlass networks after each other. Between them they place an intermediate loss. That way, the second network can learn to improve the predictions of the first network.
* Architecture visualized:
* 
* *Heatmaps*
* The output generated by the network are heatmaps, one per joint.
* Each ground truth heatmap has a small gaussian peak at the correct position of a joint, everything else has value 0.
* If a joint isn't visible, the ground truth heatmap for that joint is all zeros.
* *Other stuff*
* They use batch normalization.
* Activation functions are ReLUs.
* They use RMSprob as their optimizer.
* Implemented in Torch.
### Results
* They train and test on FLIC (only one HourGlass) and MPII (two stacked HourGlass networks).
* Training is done with augmentations (horizontal flip, up to 30 degress rotation, scaling, no translation to keep the body of interest in the center of the image).
* Evaluation is done via PCK@0.2 (i.e. percentage of predicted keypoints that are within 0.2 head sizes of their ground truth annotation (head size of the specific body)).
* Results on FLIC are at >95%.
* Results on MPII are between 80.6% (ankle) and 97.6% (head). Average is 89.4%.
* Using two stacked HourGlass networks performs around 3% better than one HourGlass network (even when adjusting for parameters).
* Training time was 5 days on a Titan X (9xx generation).
 |
DeepFace: Closing the Gap to Human-Level Performance in Face Verification
Taigman, Yaniv and Yang, Ming and Ranzato, Marc'Aurelio and Wolf, Lior
Conference and Computer Vision and Pattern Recognition - 2014 via Local Bibsonomy
Keywords: dblp
Taigman, Yaniv and Yang, Ming and Ranzato, Marc'Aurelio and Wolf, Lior
Conference and Computer Vision and Pattern Recognition - 2014 via Local Bibsonomy
Keywords: dblp
|
[link]
They describe a CNN architecture that can be used to identify a person given an image of their face.
### How
* The expected input is the image of a face (i.e. it does not search for faces in images, the faces already have to be extracted by a different method).
* *Face alignment / Frontalization*
* Target of this step: Get rid of variations within the face images, so that every face seems to look straight into the camera ("frontalized").
* 2D alignment
* They search for landmarks (fiducial points) on the face.
* They use SVRs (features: LBPs) for that.
* After every application of the SVR, the localized landmarks are used to transform/normalize the face. Then the SVR is applied again. By doing this, the locations of the landmarks are gradually refined.
* They use the detected landmarks to normalize the face images (via scaling, rotation and translation).
* 3D alignment
* The 2D alignment allows to normalize variations within the 2D-plane, not out-of-plane variations (e.g. seeing that face from its left/right side). To normalize out-of-plane variations they need a 3D transformation.
* They detect an additional 67 landmarks on the faces (again via SVRs).
* They construct a human face mesh from a dataset (USF Human-ID).
* They map the 67 landmarks to that mesh.
* They then use some more complicated steps to recover the frontalized face image.
* *CNN architecture*
* The CNN receives the frontalized face images (152x152, RGB).
* It then applies the following steps:
* Convolution, 32 filters, 11x11, ReLU (-> 32x142x142, CxHxW)
* Max pooling over 3x3, stride 2 (-> 32x71x71)
* Convolution, 16 filters, 9x9, ReLU (-> 16x63x63)
* Local Convolution, 16 filters, 9x9, ReLU (-> 16x55x55)
* Local Convolution, 16 filters, 7x7, ReLU (-> 16x25x25)
* Local Convolution, 16 filters, 5x5, ReLU (-> 16x21x21)
* Fully Connected, 4096, ReLU
* Fully Connected, 4030, Softmax
* Local Convolutions use a different set of learned weights at every "pixel" (while a normal convolution uses the same set of weights at all locations).
* They can afford to use local convolutions because of their frontalization, which roughly forces specific landmarks to be at specific locations.
* They use dropout (apparently only after the first fully connected layer).
* They normalize "the features" (probably the 4096 fully connected layer). Each component is divided by its maximum value across a training set. Additionally, the whole vector is L2-normalized. The goal of this step is to make the network less sensitive to illumination changes.
* The whole network has about 120 million parameters.
* Visualization of the architecture:
* 
* *Training*
* The network receives images, each showing a face, and is trained to classify the identity of the face (e.g. gets image of Obama, has to return "that's Obama").
* They use cross-entropy as their loss.
* *Face verification*
* In order to tell whether two images of faces show the same person they try three different methods.
* Each of these relies on the vector extracted by the first fully connected layer in the network (4096d).
* Let these vectors be `f1` (image 1) and `f2` (image 2). The methods are then:
1. Inner product between `f1` and `f2`. The classification (same person/not same person) is then done by a simple threshold.
2. Weighted X^2 (chi-squared) distance. Equation, per vector component i: `weight_i (f1[i] - f2[i])^2 / (f1[i] + f2[i])`. The vector is then fed into an SVM.
3. Siamese network. Means here simply that the absolute distance between `f1` and `f2` is calculated (`|f1-f2|`), each component is weighted by a learned weight and then the sum of the components is calculated. If the result is above a threshold, the faces are considered to show the same person.
### Results
* They train their network on the Social Face Classification (SFC) dataset. That seems to be a Facebook-internal dataset (i.e. not public) with 4.4 million faces of 4k people.
* When applied to the LFW dataset:
* Face recognition ("which person is shown in the image") (apparently they retrained the whole model on LFW for this task?):
* Simple SVM with LBP (i.e. not their network): 91.4% mean accuracy.
* Their model, with frontalization, with 2d alignment: ??? no value.
* Their model, no frontalization (only 2d alignment): 94.3% mean accuracy.
* Their model, no frontalization, no 2d alignment: 87.9% mean accuracy.
* Face verification (two images -> same/not same person) (apparently also trained on LFW? unclear):
* Method 1 (inner product + threshold): 95.92% mean accuracy.
* Method 2 (X^2 vector + SVM): 97.00% mean accurracy.
* Method 3 (siamese): Apparently 96.17% accuracy alone, and 97.25% when used in an ensemble with other methods (under special training schedule using SFC dataset).
* When applied to the YTF dataset (YouTube video frames):
* 92.5% accuracy via X^2-method.
 |
Character-based Neural Machine Translation
Costa-Jussà, Marta R. and Fonollosa, José A. R.
Association for Computational Linguistics - 2016 via Local Bibsonomy
Keywords: dblp
Costa-Jussà, Marta R. and Fonollosa, José A. R.
Association for Computational Linguistics - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* Most neural machine translation models currently operate on word vectors or one hot vectors of words.
* They instead generate the vector of each word on a character-level.
* Thereby, the model can spot character-similarities between words and treat them in a similar way.
* They do that only for the source language, not for the target language.
### How
* They treat each word of the source text on its own.
* To each word they then apply the model from [Character-aware neural language models](https://arxiv.org/abs/1508.06615), i.e. they do per word:
* Embed each character into a 620-dimensional space.
* Stack these vectors next to each other, resulting in a 2d-tensor in which each column is one of the vectors (i.e. shape `620xN` for `N` characters).
* Apply convolutions of size `620xW` to that tensor, where a few different values are used for `W` (i.e. some convolutions cover few characters, some cover many characters).
* Apply a tanh after these convolutions.
* Apply a max-over-time to the results of the convolutions, i.e. for each convolution use only the maximum value.
* Reshape to 1d-vector.
* Apply two highway-layers.
* They get 1024-dimensional vectors (one per word).
* Visualization of their steps:
* 
* Afterwards they apply the model from [Neural Machine Translation by Jointly Learning to Align and Translate](https://arxiv.org/abs/1409.0473) to these vectors, yielding a translation to a target language.
* Whenever that translation yields an unknown target-language-word ("UNK"), they replace it with the respective (untranslated) word from the source text.
### Results
* They the German-English [WMT](http://www.statmt.org/wmt15/translation-task.html) dataset.
* BLEU improvemements (compared to neural translation without character-level words):
* German-English improves by about 1.5 points.
* English-German improves by about 3 points.
* Reduction in the number of unknown target-language-words (same baseline again):
* German-English goes down from about 1500 to about 1250.
* English-German goes down from about 3150 to about 2650.
* Translation examples (Phrase = phrase-based/non-neural translation, NN = non-character-based neural translation, CHAR = theirs):
* 
 |
Convolutional Pose Machines
Wei, Shih-En and Ramakrishna, Varun and Kanade, Takeo and Sheikh, Yaser
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
Wei, Shih-En and Ramakrishna, Varun and Kanade, Takeo and Sheikh, Yaser
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a new model for human pose estimation (i.e. to lay a "skeleton" over the image of a person).
* Their model has a (more or less) recurrent architecture.
* Initial estimates of keypoint locations are refined in several steps.
* The idea of the recurrent architecture is derived from message passing, unrolled into one feed-forward model.
### How
* Architecture
* They generate the end result in multiple steps, similar to a recurrent network.
* Step 1:
* Receives the image (368x368 resolution).
* Applies a few convolutions to the image in order to predict for each pixel the likelihood of belonging to a keypoint (head, neck, right elbow, ...).
* Step 2 and later:
* (Modified) Receives the image (368x368 resolution) and the previous likelihood scores.
* (Same) Applies a few convolutions to the image in order to predict for each pixel the likelihood of belonging to a keypoint (head, neck, right elbow, ...).
* (New) Concatenates the likelihoods with the likelihoods of the previous step.
* (New) Applies a few more convolutions to the concatenation to compute the final likelihood scores.
* Visualization of the architecture:
* 
* Loss function
* The basic loss function is a simple mean squared error between the expected output maps per keypoint and the predicted ones.
* In the expected output maps they mark the correct positions of the keypoints using a small gaussian function.
* They apply losses after each step in the architecture, argueing that this helps against vanishing gradients (they don't seem to be using BN).
* The expected output maps of the first step actually have the positions of all keypoints of a certain type (e.g. neck) marked, i.e. if there are multiple people in the extracted image patch there might be multiple correct keypoint positions. Only at step 2 and later they reduce that to the expected person (i.e. one keypoint position per map).
### Results
* Example results:
* 
* Self-correction of predictions over several timesteps:
* 
* They beat existing methods on the datasets MPII, LSP and FLIC.
* Applying a loss function after each step (instead of only once after the last step) improved their results and reduced problems related to vanishing gradients.
* The effective receptive field size of each step had a significant influence on the results. They increased it to up to 300px (about 80% of the image size) and saw continuous improvements in accuracy.
* 
 |
HyperFace: A Deep Multi-task Learning Framework for Face Detection, Landmark Localization, Pose Estimation, and Gender Recognition
Ranjan, Rajeev and Patel, Vishal M. and Chellappa, Rama
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Ranjan, Rajeev and Patel, Vishal M. and Chellappa, Rama
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a single architecture that tries to solve the following tasks:
* Face localization ("Where are faces in the image?")
* Face landmark localization ("For a given face, where are its landmarks, e.g. eyes, nose and mouth?")
* Face landmark visibility estimation ("For a given face, which of its landmarks are actually visible and which of them are occluded by other objects/people?")
* Face roll, pitch and yaw estimation ("For a given face, what is its rotation on the x/y/z-axis?")
* Face gender estimation ("For a given face, which gender does the person have?")
### How
* *Pretraining the base model*
* They start with a basic model following the architecture of AlexNet.
* They train that model to classify whether the input images are faces or not faces.
* They then remove the fully connected layers, leaving only the convolutional layers.
* *Locating bounding boxes of face candidates*
* They then use a [selective search and segmentation algorithm](https://www.robots.ox.ac.uk/~vgg/rg/papers/sande_iccv11.pdf) on images to extract bounding boxes of objects.
* Each bounding box is considered a possible face.
* Each bounding box is rescaled to 227x227.
* *Feature extraction per face candidate*
* They feed each bounding box through the above mentioned pretrained network.
* They extract the activations of the network from the layers `max1` (27x27x96), `conv3` (13x13x384) and `pool5` (6x6x256).
* They apply to the first two extracted tensors (from max1, conv3) convolutions so that their tensor shapes are reduced to 6x6xC.
* They concatenate the three tensors to a 6x6x768 tensor.
* They apply a 1x1 convolution to that tensor to reduce it to 6x6x192.
* They feed the result through a fully connected layer resulting in 3072-dimensional vectors (per face candidate).
* *Classification and regression*
* They feed each 3072-dimensional vector through 5 separate networks:
1. Detection: Does the bounding box contain a face or no face. (2 outputs, i.e. yes/no)
2. Landmark Localization: What are the coordinates of landmark features (e.g. mouth, nose, ...). (21 landmarks, each 2 values for x/y = 42 outputs total)
3. Landmark Visibility: Which landmarks are visible. (21 yes/no outputs)
4. Pose estimation: Roll, pitch, yaw of the face. (3 outputs)
5. Gender estimation: Male/female face. (2 outputs)
* Each of these network contains a single fully connected layer with 512 nodes, followed by the output layer with the above mentioned number of nodes.
* *Architecture Visualization*:
* 
* *Training*
* The base model is trained once (see above).
* The feature extraction layers and the five classification/regression networks are trained afterwards (jointly).
* The loss functions for the five networks are:
1. Detection: BCE (binary cross-entropy). Detected bounding boxes that have an overlap `>=0.5` with an annotated face are considered positive samples, bounding boxes with overlap `<0.35` are considered negative samples, everything in between is ignored.
2. Landmark localization: Roughly MSE (mean squared error), with some weighting for visibility. Only bounding boxes with overlap `>0.35` are considered. Coordinates are normalized with respect to the bounding boxes center, width and height.
3. Landmark visibility: MSE (predicted visibility factor vs. expected visibility factor). Only for bounding boxes with overlap `>0.35`.
4. Pose estimation: MSE.
5. Gender estimation: BCE.
* *Testing*
* They use two postprocessing methods for detected faces:
* Iterative Region Proposals:
* They localize landmarks per face region.
* Then they compute a more appropriate face bounding box based on the localized landmarks.
* They feed that new bounding box through the network.
* They compute the face score (face / not face, i.e. number between 0 and 1) for both bounding boxes and choose the one with the higher score.
* This shrinks down bounding boxes that turned out to be too big.
* The method visualized:
* 
* Landmarks-based Non-Maximum Suppression:
* When multiple detected face bounding boxes overlap, one has to choose which of them to keep.
* A method to do that is to only keep the bounding box with the highest face-score.
* They instead use a median-of-k method.
* Their steps are:
1. Reduce every box in size so that it is a bounding box around the localized landmarks.
2. For every box, find all bounding boxes with a certain amount of overlap.
3. Among these bounding boxes, select the `k` ones with highest face score.
4. Based on these boxes, create a new box which's size is derived from the median coordinates of the landmarks.
5. Compute the median values for landmark coordinates, landmark visibility, gender, pose and use it as the respective values for the new box.
### Results
* Example results:
* 
* They test on AFW, AFWL, PASCAL, FDDB, CelebA.
* They achieve the best mean average precision values on PASCAL and AFW (compared to selected competitors).
* AFW results visualized:
* 
* Their approach achieve good performance on FDDB. It has some problems with small and/or blurry faces.
* If the feature fusion is removed from their approach (i.e. extracting features only from one fully connected layer at the end of the base network instead of merging feature maps from different convolutional layers), the accuracy of the predictions goes down.
* Their architecture ends in 5 shallow networks and shares many layers before them. If instead these networks share no or few layers, the accuracy of the predictions goes down.
* The postprocessing of bounding boxes (via Iterative Region Proposals and Landmarks-based Non-Maximum Suppression) has a quite significant influence on the performance.
* Processing time per image is 3s, of which 2s is the selective search algorithm (for the bounding boxes).
 |
Face attribute prediction using off-the-shelf CNN features
Zhong, Yang and Sullivan, Josephine and Li, Haibo
IEEE ICB - 2016 via Local Bibsonomy
Keywords: dblp
Zhong, Yang and Sullivan, Josephine and Li, Haibo
IEEE ICB - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* When using pretrained networks (like VGG) to solve tasks, one has to use features generated by these networks.
* These features come from specific layers, e.g. from the fully connected layers at the end of the network.
* They test whether the features from fully connected layers or from the last convolutional layer are better suited for face attribute prediction.
### How
* Base networks
* They use standard architectures for their test networks, specifically the architectures of FaceNet and VGG (very deep version).
* They modify these architectures to both use PReLUs.
* They do not use the pretrained weights, instead they train the networks on their own.
* They train them on the WebFace dataset (350k images, 10k different identities) to classify the identity of the shown person.
* Attribute prediction
* After training of the base networks, they train a separate SVM to predict attributes of faces.
* The datasets used for this step are CelebA (100k images, 10k identities) and LFWA (13k images, 6k identities).
* Each image in these datasets is annotated with 40 binary face attributes.
* Examples for attributes: Eyeglasses, bushy eyebrows, big lips, ...
* The features for the SVM are extracted from the base networks (i.e. feed forward a face through the network, then take the activations of a specific layer).
* The following features are tested:
* FC2: Activations of the second fully connected layer of the base network.
* FC1: As FC2, but the first fully connected layer.
* Spat 3x3: Activations of the last convolutional layer, max-pooled so that their widths and heights are both 3 (i.e. shape Cx3x3).
* Spat 1x1: Same as "Spat 3x3", but max-pooled to Cx1x1.
### Results
* The SVMs trained on "Spat 1x1" performed overall worst, the ones trained on "Spat 3x3" performed best.
* The accuracy order was roughly: `Spat 3x3 > FC1 > FC2 > Spat 1x1`.
* This effect was consistent for both networks (VGG, FaceNet) and for other training datasets as well.
* FC2 performed particularly bad for the "blurry" attribute (most likely because that was unimportant to the classification task).
* Accuracy comparison per attribute:
* 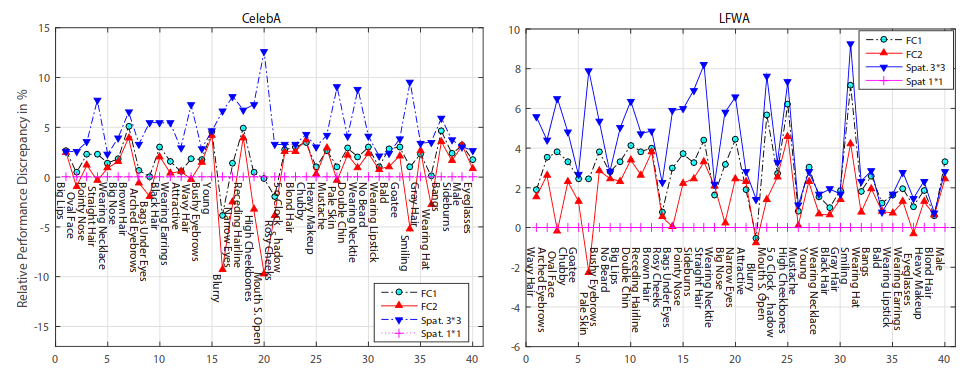
* The conclusion is, that when using pretrained networks one should not only try the last fully connected layer. Many characteristics of the input image might not appear any more in that layer (and later ones in general) as they were unimportant to the classification task.
 |
CMS-RCNN: Contextual Multi-Scale Region-based CNN for Unconstrained Face Detection
Zhu, Chenchen and Zheng, Yutong and Luu, Khoa and Savvides, Marios
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Zhu, Chenchen and Zheng, Yutong and Luu, Khoa and Savvides, Marios
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe a model to locate faces in images.
* Their model uses information from suspected face regions *and* from the corresponding suspected body regions to classify whether a region contains a face.
* The intuition is, that seeing the region around the face (specifically where the body should be) can help in estimating whether a suspected face is really a face (e.g. it might also be part of a painting, statue or doll).
### How
* Their whole model is called "CMS-RCNN" (Contextual Multi-Scale Region-CNN).
* It is based on the "Faster R-CNN" architecture.
* It uses the VGG network.
* Subparts of their model are: MS-RPN, CMS-CNN.
* MS-RPN finds candidate face regions. CMS-CNN refines their bounding boxes and classifies them (face / not face).
* **MS-RPN** (Multi-Scale Region Proposal Network)
* "Looks" at the feature maps of the network (VGG) at multiple scales (i.e. before/after pooling layers) and suggests regions for possible faces.
* Steps:
* Feed an image through the VGG network.
* Extract the feature maps of the three last convolutions that are before a pooling layer.
* Pool these feature maps so that they have the same heights and widths.
* Apply L2 normalization to each feature map so that they all have the same scale.
* Apply a 1x1 convolution to merge them to one feature map.
* Regress face bounding boxes from that feature map according to the Faster R-CNN technique.
* **CMS-CNN** (Contextual Multi-Scale CNN):
* "Looks" at feature maps of face candidates found by MS-RPN and classifies whether these regions contains faces.
* It also uses the same multi-scale technique (i.e. take feature maps from convs before pooling layers).
* It uses some area around these face regions as additional information (suspected regions of bodies).
* Steps:
* Receive face candidate regions from MS-RPN.
* Do per candidate region:
* Calculate the suspected coordinates of the body (only based on the x/y-position and size of the face region, i.e. not learned).
* Extract the feature maps of the *face* region (at multiple scales) and apply RoI-Pooling to it (i.e. convert to a fixed height and width).
* Extract the feature maps of the *body* region (at multiple scales) and apply RoI-Pooling to it (i.e. convert to a fixed height and width).
* L2-normalize each feature map.
* Concatenate the (RoI-pooled and normalized) feature maps of the face (at multiple scales) with each other (creates one tensor).
* Concatenate the (RoI-pooled and normalized) feature maps of the body (at multiple scales) with each other (creates another tensor).
* Apply a 1x1 convolution to the face tensor.
* Apply a 1x1 convolution to the body tensor.
* Apply two fully connected layers to the face tensor, creating a vector.
* Apply two fully connected layers to the body tensor, creating a vector.
* Concatenate both vectors.
* Based on that vector, make a classification of whether it is really a face.
* Based on that vector, make a regression of the face's final bounding box coordinates and dimensions.
* Note: They use in both networks the multi-scale approach in order to be able to find small or tiny faces. Otherwise, after pooling these small faces would be hard or impossible to detect.
### Results
* Adding context to the classification (i.e. the body regions) empirically improves the results.
* Their model achieves the highest recall rate on FDDB compared to other models. However, it has lower recall if only very few false positives are accepted.
* FDDB ROC curves (theirs is bold red):
* 
* Example results on FDDB:
* 
 |
Conditional Image Generation with PixelCNN Decoders
Aaron van den Oord and Nal Kalchbrenner and Oriol Vinyals and Lasse Espeholt and Alex Graves and Koray Kavukcuoglu
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV, cs.LG
First published: 2016/06/16 (7 years ago)
Abstract: This work explores conditional image generation with a new image density model based on the PixelCNN architecture. The model can be conditioned on any vector, including descriptive labels or tags, or latent embeddings created by other networks. When conditioned on class labels from the ImageNet database, the model is able to generate diverse, realistic scenes representing distinct animals, objects, landscapes and structures. When conditioned on an embedding produced by a convolutional network given a single image of an unseen face, it generates a variety of new portraits of the same person with different facial expressions, poses and lighting conditions. We also show that conditional PixelCNN can serve as a powerful decoder in an image autoencoder. Additionally, the gated convolutional layers in the proposed model improve the log-likelihood of PixelCNN to match the state-of-the-art performance of PixelRNN on ImageNet, with greatly reduced computational cost.
more
less
Aaron van den Oord and Nal Kalchbrenner and Oriol Vinyals and Lasse Espeholt and Alex Graves and Koray Kavukcuoglu
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV, cs.LG
First published: 2016/06/16 (7 years ago)
Abstract: This work explores conditional image generation with a new image density model based on the PixelCNN architecture. The model can be conditioned on any vector, including descriptive labels or tags, or latent embeddings created by other networks. When conditioned on class labels from the ImageNet database, the model is able to generate diverse, realistic scenes representing distinct animals, objects, landscapes and structures. When conditioned on an embedding produced by a convolutional network given a single image of an unseen face, it generates a variety of new portraits of the same person with different facial expressions, poses and lighting conditions. We also show that conditional PixelCNN can serve as a powerful decoder in an image autoencoder. Additionally, the gated convolutional layers in the proposed model improve the log-likelihood of PixelCNN to match the state-of-the-art performance of PixelRNN on ImageNet, with greatly reduced computational cost.
|
[link]
* PixelRNN
* PixelRNNs generate new images pixel by pixel (and row by row) via LSTMs (or other RNNs).
* Each pixel is therefore conditioned on the previously generated pixels.
* Training of PixelRNNs is slow due to the RNN-architecture (hard to parallelize).
* Previously PixelCNNs have been suggested, which use masked convolutions during training (instead of RNNs), but their image quality was worse.
* They suggest changes to PixelCNNs that improve the quality of the generated images (while still keeping them faster than RNNs).
### How
* PixelRNNs split up the distribution `p(image)` into many conditional probabilities, one per pixel, each conditioned on all previous pixels: `p(image) = <product> p(pixel i | pixel 1, pixel 2, ..., pixel i-1)`.
* PixelCNNs implement that using convolutions, which are faster to train than RNNs.
* These convolutions uses masked filters, i.e. the center weight and also all weights right and/or below the center pixel are `0` (because they are current/future values and we only want to condition on the past).
* In most generative models, several layers are stacked, ultimately ending in three float values per pixel (RGB images, one value for grayscale images). PixelRNNs (including this implementation) traditionally end in a softmax over 255 values per pixel and channel (so `3*255` per RGB pixel).
* The following image shows the application of such a convolution with the softmax output (left) and the mask for a filter (right):
* 
* Blind spot
* Using the mask on each convolutional filter effectively converts them into non-squared shapes (the green values in the image).
* Advantage: Using such non-squared convolutions prevents future values from leaking into present values.
* Disadvantage: Using such non-squared convolutions creates blind spots, i.e. for each pixel, some past values (diagonally top-right from it) cannot influence the value of that pixel.
* 
* They combine horizontal (1xN) and vertical (Nx1) convolutions to prevent that.
* Gated convolutions
* PixelRNNs via LSTMs so far created visually better images than PixelCNNs.
* They assume that one advantage of LSTMs is, that they (also) have multiplicative gates, while stacked convolutional layers only operate with summations.
* They alleviate that problem by adding gates to their convolutions:
* Equation: `output image = tanh(weights_1 * image) <element-wise product> sigmoid(weights_2 * image)`
* `*` is the convolutional operator.
* `tanh(weights_1 * image)` is a classical convolution with tanh activation function.
* `sigmoid(weights_2 * image)` are the gate values (0 = gate closed, 1 = gate open).
* `weights_1` and `weights_2` are learned.
* Conditional PixelCNNs
* When generating images, they do not only want to condition the previous values, but also on a laten vector `h` that describes the image to generate.
* The new image distribution becomes: `p(image) = <product> p(pixel i | pixel 1, pixel 2, ..., pixel i-1, h)`.
* To implement that, they simply modify the previously mentioned gated convolution, adding `h` to it:
* Equation: `output image = tanh(weights_1 * image + weights_2 . h) <element-wise product> sigmoid(weights_3 * image + weights_4 . h)`
* `.` denotes here the matrix-vector multiplication.
* PixelCNN Autoencoder
* The decoder in a standard autoencoder can be replaced by a PixelCNN, creating a PixelCNN-Autoencoder.
### Results
* They achieve similar NLL-results as PixelRNN on CIFAR-10 and ImageNet, while training about twice as fast.
* Here, "fast" means that they used 32 GPUs for 60 hours.
* Using Conditional PixelCNNs on ImageNet (i.e. adding class information to each convolution) did not improve the NLL-score, but it did improve the image quality.
* 
* They use a different neural network to create embeddings of human faces. Then they generate new faces based on these embeddings via PixelCNN.
* 
* Their PixelCNN-Autoencoder generates significantly sharper (i.e. less blurry) images than a "normal" autoencoder.
 |
InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets
Chen, Xi and Chen, Xi and Duan, Yan and Houthooft, Rein and Schulman, John and Sutskever, Ilya and Abbeel, Pieter
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
Chen, Xi and Chen, Xi and Duan, Yan and Houthooft, Rein and Schulman, John and Sutskever, Ilya and Abbeel, Pieter
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* Usually GANs transform a noise vector `z` into images. `z` might be sampled from a normal or uniform distribution.
* The effect of this is, that the components in `z` are deeply entangled.
* Changing single components has hardly any influence on the generated images. One has to change multiple components to affect the image.
* The components end up not being interpretable. Ideally one would like to have meaningful components, e.g. for human faces one that controls the hair length and a categorical one that controls the eye color.
* They suggest a change to GANs based on Mutual Information, which leads to interpretable components.
* E.g. for MNIST a component that controls the stroke thickness and a categorical component that controls the digit identity (1, 2, 3, ...).
* These components are learned in a (mostly) unsupervised fashion.
### How
* The latent code `c`
* "Normal" GANs parameterize the generator as `G(z)`, i.e. G receives a noise vector and transforms it into an image.
* This is changed to `G(z, c)`, i.e. G now receives a noise vector `z` and a latent code `c` and transforms both into an image.
* `c` can contain multiple variables following different distributions, e.g. in MNIST a categorical variable for the digit identity and a gaussian one for the stroke thickness.
* Mutual Information
* If using a latent code via `G(z, c)`, nothing forces the generator to actually use `c`. It can easily ignore it and just deteriorate to `G(z)`.
* To prevent that, they force G to generate images `x` in a way that `c` must be recoverable. So, if you have an image `x` you must be able to reliable tell which latent code `c` it has, which means that G must use `c` in a meaningful way.
* This relationship can be expressed with mutual information, i.e. the mutual information between `x` and `c` must be high.
* The mutual information between two variables X and Y is defined as `I(X; Y) = entropy(X) - entropy(X|Y) = entropy(Y) - entropy(Y|X)`.
* If the mutual information between X and Y is high, then knowing Y helps you to decently predict the value of X (and the other way round).
* If the mutual information between X and Y is low, then knowing Y doesn't tell you much about the value of X (and the other way round).
* The new GAN loss becomes `old loss - lambda * I(G(z, c); c)`, i.e. the higher the mutual information, the lower the result of the loss function.
* Variational Mutual Information Maximization
* In order to minimize `I(G(z, c); c)`, one has to know the distribution `P(c|x)` (from image to latent code), which however is unknown.
* So instead they create `Q(c|x)`, which is an approximation of `P(c|x)`.
* `I(G(z, c); c)` is then computed using a lower bound maximization, similar to the one in variational autoencoders (called "Variational Information Maximization", hence the name "InfoGAN").
* Basic equation: `LowerBoundOfMutualInformation(G, Q) = E[log Q(c|x)] + H(c) <= I(G(z, c); c)`
* `c` is the latent code.
* `x` is the generated image.
* `H(c)` is the entropy of the latent codes (constant throughout the optimization).
* Optimization w.r.t. Q is done directly.
* Optimization w.r.t. G is done via the reparameterization trick.
* If `Q(c|x)` approximates `P(c|x)` *perfectly*, the lower bound becomes the mutual information ("the lower bound becomes tight").
* In practice, `Q(c|x)` is implemented as a neural network. Both Q and D have to process the generated images, which means that they can share many convolutional layers, significantly reducing the extra cost of training Q.
### Results
* MNIST
* They use for `c` one categorical variable (10 values) and two continuous ones (uniform between -1 and +1).
* InfoGAN learns to associate the categorical one with the digit identity and the continuous ones with rotation and width.
* Applying Q(c|x) to an image and then classifying only on the categorical variable (i.e. fully unsupervised) yields 95% accuracy.
* Sampling new images with exaggerated continuous variables in the range `[-2,+2]` yields sound images (i.e. the network generalizes well).
* 
* 3D face images
* InfoGAN learns to represent the faces via pose, elevation, lighting.
* They used five uniform variables for `c`. (So two of them apparently weren't associated with anything sensible? They are not mentioned.)
* 3D chair images
* InfoGAN learns to represent the chairs via identity (categorical) and rotation or width (apparently they did two experiments).
* They used one categorical variable (four values) and one continuous variable (uniform `[-1, +1]`).
* SVHN
* InfoGAN learns to represent lighting and to spot the center digit.
* They used four categorical variables (10 values each) and two continuous variables (uniform `[-1, +1]`). (Again, a few variables were apparently not associated with anything sensible?)
* CelebA
* InfoGAN learns to represent pose, presence of sunglasses (not perfectly), hair style and emotion (in the sense of "smiling or not smiling").
* They used 10 categorical variables (10 values each). (Again, a few variables were apparently not associated with anything sensible?)
* 
 |
Improved Techniques for Training GANs
Salimans, Tim and Goodfellow, Ian J. and Zaremba, Wojciech and Cheung, Vicki and Radford, Alec and Chen, Xi
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Salimans, Tim and Goodfellow, Ian J. and Zaremba, Wojciech and Cheung, Vicki and Radford, Alec and Chen, Xi
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest some small changes to the GAN training scheme that lead to visually improved results.
* They suggest a new scoring method to compare the results of different GAN models with each other.
### How
* Feature Matching
* Usually G would be trained to mislead D as often as possible, i.e. to maximize D's output.
* Now they train G to minimize the feature distance between real and fake images. I.e. they do:
1. Pick a layer $l$ from D.
2. Forward real images through D and extract the features from layer $l$.
3. Forward fake images through D and extract the features from layer $l$.
4. Compute the squared euclidean distance between the layers and backpropagate.
* Minibatch discrimination
* They allow D to look at multiple images in the same minibatch.
* That is, they feed the features (of each image) extracted by an intermediate layer of D through a linear operation, resulting in a matrix per image.
* They then compute the L1-distances between these matrices.
* They then let D make its judgement (fake/real image) based on the features extracted from the image and these distances.
* They add this mechanism so that the diversity of images generated by G increases (which should also prevent collapses).
* Historical averaging
* They add a penalty term that punishes weights which are rather far away from their historical average values.
* I.e. the cost is `distance(current parameters, average of parameters over the last t batches)`.
* They argue that this can help the network to find equilibria that normal gradient descent would not find.
* One-sided label smoothing
* Usually one would use the labels 0 (image is fake) and 1 (image is real).
* Using smoother labels (0.1 and 0.9) seems to make networks more resistent to adversarial examples.
* So they smooth the labels of real images (apparently to 0.9?).
* Smoothing the labels of fake images would lead to (mathematical) problems in some cases, so they keep these at 0.
* Virtual Batch Normalization (VBN)
* Usually BN normalizes each example with respect to the other examples in the same batch.
* They instead normalize each example with respect to the examples in a reference batch, which was picked once at the start of the training.
* VBN is intended to reduce the dependence of each example on the other examples in the batch.
* VBN is computationally expensive, because it requires forwarding of two minibatches.
* They use VBN for their G.
* Inception Scoring
* They introduce a new scoring method for GAN results.
* Their method is based on feeding the generated images through another network, here they use Inception.
* For an image `x` and predicted classes `y` (softmax-output of Inception):
* They argue that they want `p(y|x)` to have low entropy, i.e. the model should be rather certain of seeing a class (or few classes) in the image.
* They argue that they want `p(y)` to have high entropy, i.e. the predicted classes (and therefore image contents) should have high diversity. (This seems like something that is quite a bit dependend on the used dataset?)
* They combine both measurements to the final score of `exp(KL(p(y|x) || p(y))) = exp( <sum over images> p(y|xi) * (log(p(y|xi)) - log(p(y))) )`.
* `p(y)` can be approximated as the mean of the softmax-outputs over many examples.
* Relevant python code that they use (where `part` seems to be of shape `(batch size, number of classes)`, i.e. the softmax outputs): `kl = part * (np.log(part) - np.log(np.expand_dims(np.mean(part, 0), 0))); kl = np.mean(np.sum(kl, 1)); scores.append(np.exp(kl));`
* They average this score over 50,000 generated images.
* Semi-supervised Learning
* For a dataset with K classes they extend D by K outputs (leading to K+1 outputs total).
* They then optimize two loss functions jointly:
* Unsupervised loss: The classic GAN loss, i.e. D has to predict the fake/real output correctly. (The other outputs seem to not influence this loss.)
* Supervised loss: D must correctly predict the image's class label, if it happens to be a real image and if it was annotated with a class.
* They note that training G with feature matching produces the best results for semi-supervised classification.
* They note that training G with minibatch discrimination produces significantly worse results for semi-supervised classification. (But visually the samples look better.)
* They note that using semi-supervised learning overall results in higher image quality than not using it. They speculate that this has to do with the class labels containing information about image statistics that are important to humans.
### Results
* MNIST
* They use weight normalization and white noise in D.
* Samples of high visual quality when using minibatch discrimination with semi-supervised learning.
* Very good results in semi-supervised learning when using feature matching.
* Using feature matching decreases visual quality of generated images, but improves results of semi-supervised learning.
* CIFAR-10
* D: 9-layer CNN with dropout, weight normalization.
* G: 4-layer CNN with batch normalization (so no VBN?).
* Visually very good generated samples when using minibatch discrimination with semi-supervised learning. (Probably new record quality.)
* Note: No comparison with nearest neighbours from the dataset.
* When using feature matching the results are visually not as good.
* Again, very good results in semi-supervised learning when using feature matching.
* SVHN
* Same setup as in CIFAR-10 and similar results.
* ImageNet
* They tried to generate 128x128 images and compared to DCGAN.
* They improved from "total garbage" to "garbage" (they now hit some textures, but structure is still wildly off).

*Generated CIFAR-10-like images (with minibatch discrimination and semi-supervised learning).*
 |
Synthesizing the preferred inputs for neurons in neural networks via deep generator networks
Nguyen, Anh and Dosovitskiy, Alexey and Yosinski, Jason and Brox, Thomas and Clune, Jeff
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
Nguyen, Anh and Dosovitskiy, Alexey and Yosinski, Jason and Brox, Thomas and Clune, Jeff
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a new method to generate images which maximize the activation of a specific neuron in a (trained) target network (abbreviated with "**DNN**").
* E.g. if your DNN contains a neuron that is active whenever there is a car in an image, the method should generate images containing cars.
* Such methods can be used to investigate what exactly a network has learned.
* There are plenty of methods like this one. They usually differ from each other by using different *natural image priors*.
* A natural image prior is a restriction on the generated images.
* Such a prior pushes the generated images towards realistic looking ones.
* Without such a prior it is easy to generate images that lead to high activations of specific neurons, but don't look realistic at all (e.g. they might look psychodelic or like white noise).
* That's because the space of possible images is extremely high-dimensional and can therefore hardly be covered reliably by a single network. Note also that training datasets usually only show a very limited subset of all possible images.
* Their work introduces a new natural image prior.
### How
* Usually, if one wants to generate images that lead to high activations, the basic/naive method is to:
1. Start with a noise image,
2. Feed that image through DNN,
3. Compute an error that is high if the activation of the specified neuron is low (analogous for high activation),
4. Backpropagate the error through DNN,
5. Change the noise image according to the gradient,
6. Repeat.
* So, the noise image is basically treated like weights in the network.
* Their alternative method is based on a Generator network **G**.
* That G is trained according to the method described in [Generating Images with Perceptual Similarity Metrics based on Deep Networks].
* Very rough outline of that method:
* First, a pretrained network **E** is given (they picked CaffeNet, which is a variation of AlexNet).
* G then has to learn to inverse E, i.e. G receives per image the features extracted by a specific layer in E (e.g. the last fully connected layer before the output) and has to generate (recreate) the image from these features.
* Their modified steps are:
1. *(New step)* Start with a noise vector,
2. *(New step)* Feed that vector through G resulting in an image,
3. *(Same)* Feed that image through DNN,
4. *(Same)* Compute an error that is low if the activation of the specified neuron is high (analogous for low activations),
5. *(Same)* Backpropagate the error through DNN,
6. *(Modified)* Change the noise *vector* according to the gradient,
7. *(Same)* Repeat.
* Visualization of their architecture:
* 
* Additionally they do:
* Apply an L2 norm to the noise vector, which adds pressure to each component to take low values. They say that this improved the results.
* Clip each component of the noise vector to a range `[0, a]`, which improved the results significantly.
* The range starts at `0`, because the network (E) inverted by their Generator (G) is based on ReLUs.
* `a` is derived from test images fed through E and set to 3 standard diviations of the mean activation of that component (recall that the "noise" vector mirrors a specific layer in E).
* They argue that this clipping is similar to a prior on the noise vector components. That prior reflects likely values of the layer in E that is used for the noise vector.
### Results
* Examples of generated images:
* 
* Early vs. late layers
* For G they have to pick a specific layer from E that G has to invert. They found that using "later" layers (e.g. the fully connected layers at the end) produced images with more reasonable overall structure than using "early" layers (e.g. first convolutional layers). Early layers led to repeating structures.
* Datasets and architectures
* Both G and DNN have to be trained on datasets.
* They found that these networks can actually be trained on different datasets, the results will still look good.
* However, they found that the architectures of DNN and E should be similar to create the best looking images (though this might also be down to depth of the tested networks).
* Verification that the prior can generate any image
* They tested whether the generated images really show what the DNN-neurons prefer and not what the Generator/prior prefers.
* To do that, they retrained DNNs on images that were both directly from the dataset as well as images that were somehow modified.
* Those modifications were:
* Treated RGB images as if they were BGR (creating images with weird colors).
* Copy-pasted areas in the images around (creating mosaics).
* Blurred the images (with gaussian blur).
* The DNNs were then trained to classify the "normal" images into 1000 classes and the modified images into 1000 other classes (2000 total).
* So at the end there were (in the same DNN) neurons reacting strongly to specific classes of unmodified images and other neurons that reacted strongly to specific classes of modified images.
* When generating images to maximize activations of specific neurons, the Generator was able to create both modified and unmodified images. Though it seemed to have some trouble with blurring.
* That shows that the generated images probably indeed show what the DNN has learned and not just what G has learned.
* Uncanonical images
* The method can sometimes generate uncanonical images (e.g. instead of a full dog just blobs of texture).
* They found that this seems to be mostly the case when the dataset images have uncanonical pose, i.e. are very diverse/multi-modal.
 |
FractalNet: Ultra-Deep Neural Networks without Residuals
Larsson, Gustav and Maire, Michael and Shakhnarovich, Gregory
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Larsson, Gustav and Maire, Michael and Shakhnarovich, Gregory
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe an architecture for deep CNNs that contains short and long paths. (Short = few convolutions between input and output, long = many convolutions between input and output)
* They achieve comparable accuracy to residual networks, without using residuals.
### How
* Basic principle:
* They start with two branches. The left branch contains one convolutional layer, the right branch contains a subnetwork.
* That subnetwork again contains a left branch (one convolutional layer) and a right branch (a subnetwork).
* This creates a recursion.
* At the last step of the recursion they simply insert two convolutional layers as the subnetwork.
* Each pair of branches (left and right) is merged using a pair-wise mean. (Result: One of the branches can be skipped or removed and the result after the merge will still be sound.)
* Their recursive expansion rule (left) and architecture (middle and right) visualized:

* Blocks:
* Each of the recursively generated networks is one block.
* They chain five blocks in total to create the network that they use for their experiments.
* After each block they add a max pooling layer.
* Their first block uses 64 filters per convolutional layer, the second one 128, followed by 256, 512 and again 512.
* Drop-path:
* They randomly dropout whole convolutional layers between merge-layers.
* They define two methods for that:
* Local drop-path: Drops each input to each merge layer with a fixed probability, but at least one always survives. (See image, first three examples.)
* Global drop-path: Drops convolutional layers so that only a single columns (and thereby path) in the whole network survives. (See image, right.)
* Visualization:
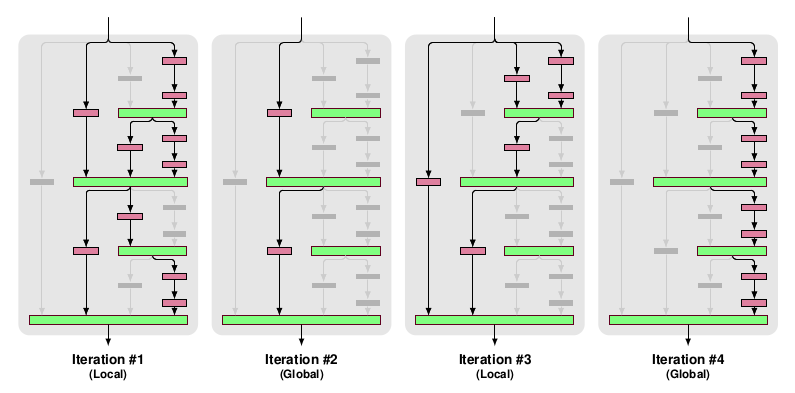
### Results
* They test on CIFAR-10, CIFAR-100 and SVHN with no or mild (crops, flips) augmentation.
* They add dropout at the start of each block (probabilities: 0%, 10%, 20%, 30%, 40%).
* They use for 50% of the batches local drop-path at 15% and for the other 50% global drop-path.
* They achieve comparable accuracy to ResNets (a bit behind them actually).
* Note: The best ResNet that they compare to is "ResNet with Identity Mappings". They don't compare to Wide ResNets, even though they perform best.
* If they use image augmentations, dropout and drop-path don't seem to provide much benefit (only small improvement).
* If they extract the deepest column and test on that one alone, they achieve nearly the same performance as with the whole network.
* They derive from that, that their fractal architecture is actually only really used to help that deepest column to learn anything. (Without shorter paths it would just learn nothing due to vanishing gradients.)
 |
PlaNet - Photo Geolocation with Convolutional Neural Networks
Weyand, Tobias and Kostrikov, Ilya and Philbin, James
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
Weyand, Tobias and Kostrikov, Ilya and Philbin, James
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe a convolutional network that takes in photos and returns where (on the planet) these photos were likely made.
* The output is a distribution over locations around the world (so not just one single location). This can be useful in the case of ambiguous images.
### How
* Basic architecture
* They simply use the Inception architecture for their model.
* They have 97M parameters.
* Grid
* The network uses a grid of cells over the planet.
* For each photo and every grid cell it returns the likelihood that the photo was made within the region covered by the cell (simple softmax layer).
* The naive way would be to use a regular grid around the planet (i.e. a grid in which all cells have the same size).
* Possible disadvantages:
* In places where lots of photos are taken you still have the same grid cell size as in places where barely any photos are taken.
* Maps are often distorted towards the poles (countries are represented much larger than they really are). This will likely affect the grid cells too.
* They instead use an adaptive grid pattern based on S2 cells.
* S2 cells interpret the planet as a sphere and project a cube onto it.
* The 6 sides of the cube are then partitioned using quad trees, creating the grid cells.
* They don't use the same depth for all quad trees. Instead they subdivide them only if their leafs contain enough photos (based on their dataset of geolocated images).
* They remove some cells for which their dataset does not contain enough images, e.g. cells on oceans. (They also remove these images from the dataset. They don't say how many images are affected by this.)
* They end up with roughly 26k cells, some of them reaching the street level of major cities.
* Visualization of their cells:
* Training
* For each example photo that they feed into the network, they set the correct grid cell to `1.0` and all other grid cells to `0.0`.
* They train on a dataset of 126M images with Exif geolocation information. The images were collected from all over the web.
* They used Adagrad.
* They trained on 200 CPUs for 2.5 months.
* Album network
* For photo albums they develop variations of their network.
* They do that because albums often contain images that are very hard to geolocate on their own, but much easier if the other images of the album are seen.
* They use LSTMs for their album network.
* The simplest one just iterates over every photo, applies their previously described model to it and extracts the last layer (before output) from that model. These vectors (one per image) are then fed into an LSTM, which is trained to predict (again) the grid cell location per image.
* More complicated versions use multiple passes or are bidirectional LSTMs (to use the information from the last images to classify the first ones in the album).
### Results
* They beat previous models (based on hand-engineered features or nearest neighbour methods) by a significant margin.
* In a small experiment they can beat experienced humans in geoguessr.com.
* Based on a dataset of 2.3M photos from Flickr, their method correctly predicts the country where the photo was made in 30% of all cases (top-1; top-5: about 50%). City-level accuracy is about 10% (top-1; top-5: about 18%).
* Example predictions (using in coarser grid with 354 cells):

* Using the LSTM-technique for albums significantly improves prediction accuracy for these images.
 |
Adam: A Method for Stochastic Optimization
Kingma, Diederik P. and Ba, Jimmy
arXiv e-Print archive - 2014 via Local Bibsonomy
Keywords: dblp
Kingma, Diederik P. and Ba, Jimmy
arXiv e-Print archive - 2014 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a new stochastic optimization method, similar to the existing SGD, Adagrad or RMSProp.
* Stochastic optimization methods have to find parameters that minimize/maximize a stochastic function.
* A function is stochastic (non-deterministic), if the same set of parameters can generate different results. E.g. the loss of different mini-batches can differ, even when the parameters remain unchanged. Even for the same mini-batch the results can change due to e.g. dropout.
* Their method tends to converge faster to optimal parameters than the existing competitors.
* Their method can deal with non-stationary distributions (similar to e.g. SGD, Adadelta, RMSProp).
* Their method can deal with very sparse or noisy gradients (similar to e.g. Adagrad).
### How
* Basic principle
* Standard SGD just updates the parameters based on `parameters = parameters - learningRate * gradient`.
* Adam operates similar to that, but adds more "cleverness" to the rule.
* It assumes that the gradient values have means and variances and tries to estimate these values.
* Recall here that the function to optimize is stochastic, so there is some randomness in the gradients.
* The mean is also called "the first moment".
* The variance is also called "the second (raw) moment".
* Then an update rule very similar to SGD would be `parameters = parameters - learningRate * means`.
* They instead use the update rule `parameters = parameters - learningRate * means/sqrt(variances)`.
* They call `means/sqrt(variances)` a 'Signal to Noise Ratio'.
* Basically, if the variance of a specific parameter's gradient is high, it is pretty unclear how it should be changend. So we choose a small step size in the update rule via `learningRate * mean/sqrt(highValue)`.
* If the variance is low, it is easier to predict how far to "move", so we choose a larger step size via `learningRate * mean/sqrt(lowValue)`.
* Exponential moving averages
* In order to approximate the mean and variance values you could simply save the last `T` gradients and then average the values.
* That however is a pretty bad idea, because it can lead to high memory demands (e.g. for millions of parameters in CNNs).
* A simple average also has the disadvantage, that it would completely ignore all gradients before `T` and weight all of the last `T` gradients identically. In reality, you might want to give more weight to the last couple of gradients.
* Instead, they use an exponential moving average, which fixes both problems and simply updates the average at every timestep via the formula `avg = alpha * avg + (1 - alpha) * avg`.
* Let the gradient at timestep (batch) `t` be `g`, then we can approximate the mean and variance values using:
* `mean = beta1 * mean + (1 - beta1) * g`
* `variance = beta2 * variance + (1 - beta2) * g^2`.
* `beta1` and `beta2` are hyperparameters of the algorithm. Good values for them seem to be `beta1=0.9` and `beta2=0.999`.
* At the start of the algorithm, `mean` and `variance` are initialized to zero-vectors.
* Bias correction
* Initializing the `mean` and `variance` vectors to zero is an easy and logical step, but has the disadvantage that bias is introduced.
* E.g. at the first timestep, the mean of the gradient would be `mean = beta1 * 0 + (1 - beta1) * g`, with `beta1=0.9` then: `mean = 0.9 * g`. So `0.9g`, not `g`. Both the mean and the variance are biased (towards 0).
* This seems pretty harmless, but it can be shown that it lowers the convergence speed of the algorithm by quite a bit.
* So to fix this pretty they perform bias-corrections of the mean and the variance:
* `correctedMean = mean / (1-beta1^t)` (where `t` is the timestep).
* `correctedVariance = variance / (1-beta2^t)`.
* Both formulas are applied at every timestep after the exponential moving averages (they do not influence the next timestep).

 |
Generating images with recurrent adversarial networks
Daniel Jiwoong Im and Chris Dongjoo Kim and Hui Jiang and Roland Memisevic
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.CV
First published: 2016/02/16 (8 years ago)
Abstract: Gatys et al. (2015) showed that optimizing pixels to match features in a convolutional network with respect reference image features is a way to render images of high visual quality. We show that unrolling this gradient-based optimization yields a recurrent computation that creates images by incrementally adding onto a visual "canvas". We propose a recurrent generative model inspired by this view, and show that it can be trained using adversarial training to generate very good image samples. We also propose a way to quantitatively compare adversarial networks by having the generators and discriminators of these networks compete against each other.
more
less
Daniel Jiwoong Im and Chris Dongjoo Kim and Hui Jiang and Roland Memisevic
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.CV
First published: 2016/02/16 (8 years ago)
Abstract: Gatys et al. (2015) showed that optimizing pixels to match features in a convolutional network with respect reference image features is a way to render images of high visual quality. We show that unrolling this gradient-based optimization yields a recurrent computation that creates images by incrementally adding onto a visual "canvas". We propose a recurrent generative model inspired by this view, and show that it can be trained using adversarial training to generate very good image samples. We also propose a way to quantitatively compare adversarial networks by having the generators and discriminators of these networks compete against each other.
|
[link]
* What
* They describe a new architecture for GANs.
* The architecture is based on letting the Generator (G) create images in multiple steps, similar to DRAW.
* They also briefly suggest a method to compare the quality of the results of different generators with each other.
* How
* In a classic GAN one samples a noise vector `z`, feeds that into a Generator (`G`), which then generates an image `x`, which is then fed through the Discriminator (`D`) to estimate its quality.
* Their method operates in basically the same way, but internally G is changed to generate images in multiple time steps.
* Outline of how their G operates:
* Time step 0:
* Input: Empty image `delta C-1`, randomly sampled `z`.
* Feed `delta C-1` through a number of downsampling convolutions to create a tensor. (Not very useful here, as the image is empty. More useful in later timesteps.)
* Feed `z` through a number of upsampling convolutions to create a tensor (similar to DCGAN).
* Concat the output of the previous two steps.
* Feed that concatenation through a few more convolutions.
* Output: `delta C0` (changes to apply to the empty starting canvas).
* Time step 1 (and later):
* Input: Previous change `delta C0`, randomly sampled `z` (can be the same as in step 0).
* Feed `delta C0` through a number of downsampling convolutions to create a tensor.
* Feed `z` through a number of upsampling convolutions to create a tensor (similar to DCGAN).
* Concat the output of the previous two steps.
* Feed that concatenation through a few more convolutions.
* Output: `delta C1` (changes to apply to the empty starting canvas).
* At the end, after all timesteps have been performed:
* Create final output image by summing all the changes, i.e. `delta C0 + delta C1 + ...`, which basically means `empty start canvas + changes from time step 0 + changes from time step 1 + ...`.
* Their architecture as an image:
* 
* Comparison measure
* They suggest a new method to compare GAN results with each other.
* They suggest to train pairs of G and D, e.g. for two pairs (G1, D1), (G2, D2). Then they let the pairs compete with each other.
* To estimate the quality of D they suggest `r_test = errorRate(D1, testset) / errorRate(D2, testset)`. ("Which D is better at spotting that the test set images are real images?")
* To estimate the quality of the generated samples they suggest `r_sample = errorRate(D1, images by G2) / errorRate(D2, images by G1)`. ("Which G is better at fooling an unknown D, i.e. possibly better at generating life-like images?")
* They suggest to estimate which G is better using r_sample and then to estimate how valid that result is using r_test.
* Results
* Generated images of churches, with timesteps 1 to 5:
* 
* Overfitting
* They saw no indication of overfitting in the sense of memorizing images from the training dataset.
* They however saw some indication of G just interpolating between some good images and of G reusing small image patches in different images.
* Randomness of noise vector `z`:
* Sampling the noise vector once seems to be better than resampling it at every timestep.
* Resampling it at every time step often led to very similar looking output images.
 |
Adversarially Learned Inference
Vincent Dumoulin and Ishmael Belghazi and Ben Poole and Alex Lamb and Martin Arjovsky and Olivier Mastropietro and Aaron Courville
arXiv e-Print archive - 2016 via Local arXiv
Keywords: stat.ML, cs.LG
First published: 2016/06/02 (7 years ago)
Abstract: We introduce the adversarially learned inference (ALI) model, which jointly learns a generation network and an inference network using an adversarial process. The generation network maps samples from stochastic latent variables to the data space while the inference network maps training examples in data space to the space of latent variables. An adversarial game is cast between these two networks and a discriminative network that is trained to distinguish between joint latent/data-space samples from the generative network and joint samples from the inference network. We illustrate the ability of the model to learn mutually coherent inference and generation networks through the inspections of model samples and reconstructions and confirm the usefulness of the learned representations by obtaining a performance competitive with other recent approaches on the semi-supervised SVHN task.
more
less
Vincent Dumoulin and Ishmael Belghazi and Ben Poole and Alex Lamb and Martin Arjovsky and Olivier Mastropietro and Aaron Courville
arXiv e-Print archive - 2016 via Local arXiv
Keywords: stat.ML, cs.LG
First published: 2016/06/02 (7 years ago)
Abstract: We introduce the adversarially learned inference (ALI) model, which jointly learns a generation network and an inference network using an adversarial process. The generation network maps samples from stochastic latent variables to the data space while the inference network maps training examples in data space to the space of latent variables. An adversarial game is cast between these two networks and a discriminative network that is trained to distinguish between joint latent/data-space samples from the generative network and joint samples from the inference network. We illustrate the ability of the model to learn mutually coherent inference and generation networks through the inspections of model samples and reconstructions and confirm the usefulness of the learned representations by obtaining a performance competitive with other recent approaches on the semi-supervised SVHN task.
|
[link]
* They suggest a new architecture for GANs.
* Their architecture adds another Generator for a reverse branch (from images to noise vector `z`).
* Their architecture takes some ideas from VAEs/variational neural nets.
* Overall they can improve on the previous state of the art (DCGAN).
### How
* Architecture
* Usually, in GANs one feeds a noise vector `z` into a Generator (G), which then generates an image (`x`) from that noise.
* They add a reverse branch (G2), in which another Generator takes a real image (`x`) and generates a noise vector `z` from that.
* The noise vector can now be viewed as a latent space vector.
* Instead of letting G2 generate *discrete* values for `z` (as it is usually done), they instead take the approach commonly used VAEs and use *continuous* variables instead.
* That is, if `z` represents `N` latent variables, they let G2 generate `N` means and `N` variances of gaussian distributions, with each distribution representing one value of `z`.
* So the model could e.g. represent something along the lines of "this face looks a lot like a female, but with very low probability could also be male".
* Training
* The Discriminator (D) is now trained on pairs of either `(real image, generated latent space vector)` or `(generated image, randomly sampled latent space vector)` and has to tell them apart from each other.
* Both Generators are trained to maximally confuse D.
* G1 (from `z` to `x`) confuses D maximally, if it generates new images that (a) look real and (b) fit well to the latent variables in `z` (e.g. if `z` says "image contains a cat", then the image should contain a cat).
* G2 (from `x` to `z`) confuses D maximally, if it generates good latent variables `z` that fit to the image `x`.
* Continuous variables
* The variables in `z` follow gaussian distributions, which makes the training more complicated, as you can't trivially backpropagate through gaussians.
* When training G1 (from `z` to `x`) the situation is easy: You draw a random `z`-vector following a gaussian distribution (`N(0, I)`). (This is basically the same as in "normal" GANs. They just often use uniform distributions instead.)
* When training G2 (from `x` to `z`) the situation is a bit harder.
* Here we need to use the reparameterization trick here.
* That roughly means, that G2 predicts the means and variances of the gaussian variables in `z` and then we draw a sample of `z` according to exactly these means and variances.
* That sample gives us discrete values for our backpropagation.
* If we do that sampling often enough, we get a good approximation of the true gradient (of the continuous variables). (Monte Carlo approximation.)
* Results
* Images generated based on Celeb-A dataset:
* 
* Left column per pair: Real image, right column per pair: reconstruction (`x -> z` via G2, then `z -> x` via G1)
* 
* Reconstructions of SVHN, notice how the digits often stay the same, while the font changes:
* 
* CIFAR-10 samples, still lots of errors, but some quite correct:
* 
 |
Resnet in Resnet: Generalizing Residual Architectures
Targ, Sasha and Almeida, Diogo and Lyman, Kevin
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Targ, Sasha and Almeida, Diogo and Lyman, Kevin
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe an architecture that merges classical convolutional networks and residual networks.
* The architecture can (theoretically) learn anything that a classical convolutional network or a residual network can learn, as it contains both of them.
* The architecture can (theoretically) learn how many convolutional layers it should use per residual block (up to the amount of convolutional layers in the whole network).
### How
* Just like residual networks, they have "blocks". Each block contains convolutional layers.
* Each block contains residual units and non-residual units.
* They have two "streams" of data in their network (just matrices generated by each block):
* Residual stream: The residual blocks write to this stream (i.e. it's their output).
* Transient stream: The non-residual blocks write to this stream.
* Residual and non-residual layers receive *both* streams as input, but only write to *their* stream as output.
* Their architecture visualized:

* Because of this architecture, their model can learn the number of layers per residual block (though BN and ReLU might cause problems here?):

* The easiest way to implement this should be along the lines of the following (some of the visualized convolutions can be merged):
* Input of size CxHxW (both streams, each C/2 planes)
* Concat
* Residual block: Apply C/2 convolutions to the C input planes, with shortcut addition afterwards.
* Transient block: Apply C/2 convolutions to the C input planes.
* Apply BN
* Apply ReLU
* Output of size CxHxW.
* The whole operation can also be implemented with just a single convolutional layer, but then one has to make sure that some weights stay at zero.
### Results
* They test on CIFAR-10 and CIFAR-100.
* They search for optimal hyperparameters (learning rate, optimizer, L2 penalty, initialization method, type of shortcut connection in residual blocks) using a grid search.
* Their model improves upon a wide ResNet and an equivalent non-residual CNN by a good margin (CIFAR-10: 0.5-1%, CIFAR-100: 1-2%).
 |
Rank Ordered Autoencoders
Paul Bertens
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, stat.ML, I.2.6; I.5.1; I.4.2
First published: 2016/05/05 (7 years ago)
Abstract: A new method for the unsupervised learning of sparse representations using autoencoders is proposed and implemented by ordering the output of the hidden units by their activation value and progressively reconstructing the input in this order. This can be done efficiently in parallel with the use of cumulative sums and sorting only slightly increasing the computational costs. Minimizing the difference of this progressive reconstruction with respect to the input can be seen as minimizing the number of active output units required for the reconstruction of the input. The model thus learns to reconstruct optimally using the least number of active output units. This leads to high sparsity without the need for extra hyperparameters, the amount of sparsity is instead implicitly learned by minimizing this progressive reconstruction error. Results of the trained model are given for patches of the CIFAR10 dataset, showing rapid convergence of features and extremely sparse output activations while maintaining a minimal reconstruction error and showing extreme robustness to overfitting. Additionally the reconstruction as function of number of active units is presented which shows the autoencoder learns a rank order code over the input where the highest ranked units correspond to the highest decrease in reconstruction error.
more
less
Paul Bertens
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, stat.ML, I.2.6; I.5.1; I.4.2
First published: 2016/05/05 (7 years ago)
Abstract: A new method for the unsupervised learning of sparse representations using autoencoders is proposed and implemented by ordering the output of the hidden units by their activation value and progressively reconstructing the input in this order. This can be done efficiently in parallel with the use of cumulative sums and sorting only slightly increasing the computational costs. Minimizing the difference of this progressive reconstruction with respect to the input can be seen as minimizing the number of active output units required for the reconstruction of the input. The model thus learns to reconstruct optimally using the least number of active output units. This leads to high sparsity without the need for extra hyperparameters, the amount of sparsity is instead implicitly learned by minimizing this progressive reconstruction error. Results of the trained model are given for patches of the CIFAR10 dataset, showing rapid convergence of features and extremely sparse output activations while maintaining a minimal reconstruction error and showing extreme robustness to overfitting. Additionally the reconstruction as function of number of active units is presented which shows the autoencoder learns a rank order code over the input where the highest ranked units correspond to the highest decrease in reconstruction error.
|
[link]
* Autoencoders typically have some additional criterion that pushes them towards learning meaningful representations.
* E.g. L1-Penalty on the code layer (z), Dropout on z, Noise on z.
* Often, representations with sparse activations are considered meaningful (so that each activation reflects are clear concept).
* This paper introduces another technique that leads to sparsity.
* They use a rank ordering on z.
* The first (according to the ranking) activations have to do most of the reconstruction work of the data (i.e. image).
### How
* Basic architecture:
* They use an Autoencoder architecture: Input -> Encoder -> z -> Decoder -> Output.
* Their encoder and decoder seem to be empty, i.e. z is the only hidden layer in the network.
* Their output is not just one image (or whatever is encoded), instead they generate one for every unit in layer z.
* Then they order these outputs based on the activation of the units in z (rank ordering), i.e. the output of the unit with the highest activation is placed in the first position, the output of the unit with the 2nd highest activation gets the 2nd position and so on.
* They then generate the final output image based on a cumulative sum. So for three reconstructed output images `I1, I2, I3` (rank ordered that way) they would compute `final image = I1 + (I1+I2) + (I1+I2+I3)`.
* They then compute the error based on that reconstruction (`reconstruction - input image`) and backpropagate it.
* Cumulative sum:
* Using the cumulative sum puts most optimization pressure on units with high activation, as they have the largest influence on the reconstruction error.
* The cumulative sum is best optimized by letting few units have high activations and generate most of the output (correctly). All the other units have ideally low to zero activations and low or no influence on the output. (Though if the output generated by the first units is wrong, you should then end up with an extremely high cumulative error sum...)
* So their `z` coding should end up with few but high activations, i.e. it should become very sparse.
* The cumulative generates an individual error per output, while an ordinary sum generates the same error for every output. They argue that this "blurs" the error less.
* To avoid blow ups in their network they use TReLUs, which saturate below 0 and above 1, i.e. `min(1, max(0, input))`.
* They use a custom derivative function for the TReLUs, which is dependent on both the input value of the unit and its gradient. Basically, if the input is `>1` (saturated) and the error is high, then the derivative pushes the weight down, so that the input gets into the unsaturated regime. Similarly for input values `<0` (pushed up). If the input value is between 0 and 1 and/or the error is low, then nothing is changed.
* They argue that the algorithmic complexity of the rank ordering should be low, due to sorts being `O(n log(n))`, where `n` is the number of hidden units in `z`.
### Results
* They autoencode 7x7 patches from CIFAR-10.
* They get very sparse activations.
* Training and test loss develop identically, i.e. no overfitting.
 |
Wide Residual Networks
Sergey Zagoruyko and Nikos Komodakis
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV, cs.LG, cs.NE
First published: 2016/05/23 (7 years ago)
Abstract: Deep residual networks were shown to be able to scale up to thousands of layers and still have improving performance. However, each fraction of a percent of improved accuracy costs nearly doubling the number of layers, and so training very deep residual networks has a problem of diminishing feature reuse, which makes these networks very slow to train. To tackle these problems, in this paper we conduct a detailed experimental study on the architecture of ResNet blocks, based on which we propose a novel architecture where we decrease depth and increase width of residual networks. We call the resulting network structures wide residual networks (WRNs) and show that these are far superior over their commonly used thin and very deep counterparts. For example, we demonstrate that even a simple 16-layer-deep wide residual network outperforms in accuracy and efficiency all previous deep residual networks, including thousand-layer-deep networks, achieving new state-of-the-art results on CIFAR-10, CIFAR-100 and SVHN.
more
less
Sergey Zagoruyko and Nikos Komodakis
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV, cs.LG, cs.NE
First published: 2016/05/23 (7 years ago)
Abstract: Deep residual networks were shown to be able to scale up to thousands of layers and still have improving performance. However, each fraction of a percent of improved accuracy costs nearly doubling the number of layers, and so training very deep residual networks has a problem of diminishing feature reuse, which makes these networks very slow to train. To tackle these problems, in this paper we conduct a detailed experimental study on the architecture of ResNet blocks, based on which we propose a novel architecture where we decrease depth and increase width of residual networks. We call the resulting network structures wide residual networks (WRNs) and show that these are far superior over their commonly used thin and very deep counterparts. For example, we demonstrate that even a simple 16-layer-deep wide residual network outperforms in accuracy and efficiency all previous deep residual networks, including thousand-layer-deep networks, achieving new state-of-the-art results on CIFAR-10, CIFAR-100 and SVHN.
|
[link]
* The authors start with a standard ResNet architecture (i.e. residual network has suggested in "Identity Mappings in Deep Residual Networks").
* Their residual block:

* Several residual blocks of 16 filters per conv-layer, followed by 32 and then 64 filters per conv-layer.
* They empirically try to answer the following questions:
* How many residual blocks are optimal? (Depth)
* How many filters should be used per convolutional layer? (Width)
* How many convolutional layers should be used per residual block?
* Does Dropout between the convolutional layers help?
### Results
* *Layers per block and kernel sizes*:
* Using 2 convolutional layers per residual block seems to perform best:

* Using 3x3 kernel sizes for both layers seems to perform best.
* However, using 3 layers with kernel sizes 3x3, 1x1, 3x3 and then using less residual blocks performs nearly as good and decreases the required time per batch.
* *Width and depth*:
* Increasing the width considerably improves the test error.
* They achieve the best results (on CIFAR-10) when decreasing the depth to 28 convolutional layers, with each having 10 times their normal width (i.e. 16\*10 filters, 32\*10 and 64\*10):

* They argue that their results show no evidence that would support the common theory that thin and deep networks somehow regularized better than wide and shallow(er) networks.
* *Dropout*:
* They use dropout with p=0.3 (CIFAR) and p=0.4 (SVHN).
* On CIFAR-10 dropout doesn't seem to consistently improve test error.
* On CIFAR-100 and SVHN dropout seems to lead to improvements that are either small (wide and shallower net, i.e. depth=28, width multiplier=10) or significant (ResNet-50).

* They also observed oscillations in error (both train and test) during the training. Adding dropout decreased these oscillations.
* *Computational efficiency*:
* Applying few big convolutions is much more efficient on GPUs than applying many small ones sequentially.
* Their network with the best test error is 1.6 times faster than ResNet-1001, despite having about 3 times more parameters.
 |
Identity Mappings in Deep Residual Networks
He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* The authors reevaluate the original residual design of neural networks.
* They compare various architectures of residual units and actually find one that works quite a bit better.
### How
* The new variation starts the transformation branch of each residual unit with BN and a ReLU.
* It removes BN and ReLU after the last convolution.
* As a result, the information from previous layers can flow completely unaltered through the shortcut branch of each residual unit.
* The image below shows some variations (of the position of BN and ReLU) that they tested. The new and better design is on the right:
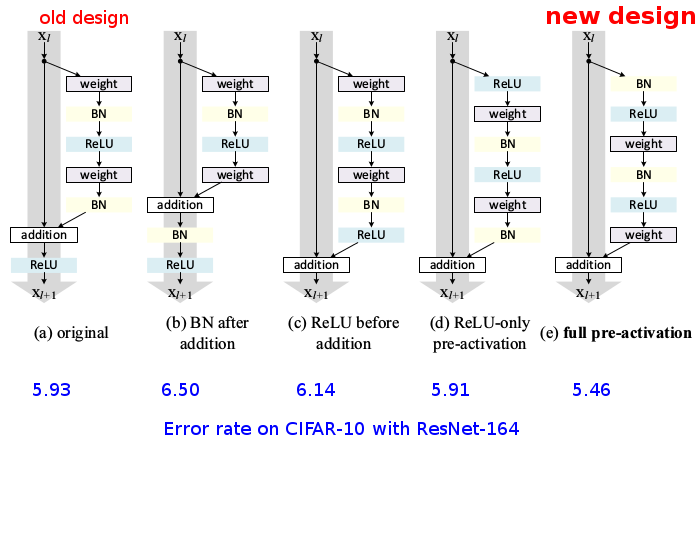
* They also tried various alternative designs for the shortcut connections. However, all of these designs performed worse than the original one. Only one (d) came close under certain conditions. Therefore, the recommendation is to stick with the old/original design.
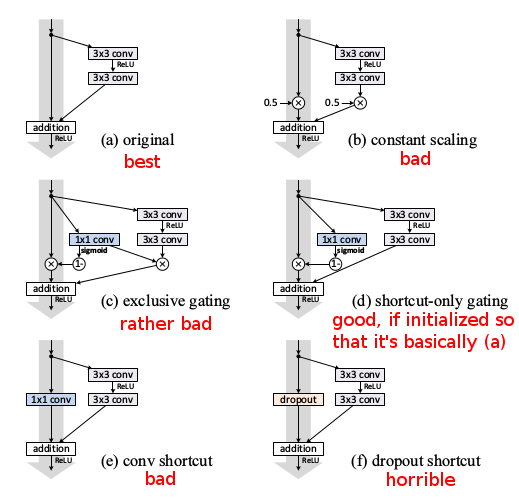
### Results
* Significantly faster training for very deep residual networks (1001 layers).
* Better regularization due to the placement of BN.
* CIFAR-10 and CIFAR-100 results, old vs. new design:
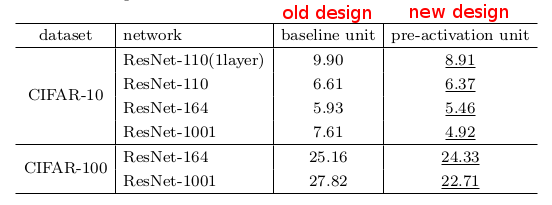
 |
Swapout: Learning an ensemble of deep architectures
Saurabh Singh and Derek Hoiem and David Forsyth
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV, cs.LG, cs.NE
First published: 2016/05/20 (7 years ago)
Abstract: We describe Swapout, a new stochastic training method, that outperforms ResNets of identical network structure yielding impressive results on CIFAR-10 and CIFAR-100. Swapout samples from a rich set of architectures including dropout, stochastic depth and residual architectures as special cases. When viewed as a regularization method swapout not only inhibits co-adaptation of units in a layer, similar to dropout, but also across network layers. We conjecture that swapout achieves strong regularization by implicitly tying the parameters across layers. When viewed as an ensemble training method, it samples a much richer set of architectures than existing methods such as dropout or stochastic depth. We propose a parameterization that reveals connections to exiting architectures and suggests a much richer set of architectures to be explored. We show that our formulation suggests an efficient training method and validate our conclusions on CIFAR-10 and CIFAR-100 matching state of the art accuracy. Remarkably, our 32 layer wider model performs similar to a 1001 layer ResNet model.
more
less
Saurabh Singh and Derek Hoiem and David Forsyth
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV, cs.LG, cs.NE
First published: 2016/05/20 (7 years ago)
Abstract: We describe Swapout, a new stochastic training method, that outperforms ResNets of identical network structure yielding impressive results on CIFAR-10 and CIFAR-100. Swapout samples from a rich set of architectures including dropout, stochastic depth and residual architectures as special cases. When viewed as a regularization method swapout not only inhibits co-adaptation of units in a layer, similar to dropout, but also across network layers. We conjecture that swapout achieves strong regularization by implicitly tying the parameters across layers. When viewed as an ensemble training method, it samples a much richer set of architectures than existing methods such as dropout or stochastic depth. We propose a parameterization that reveals connections to exiting architectures and suggests a much richer set of architectures to be explored. We show that our formulation suggests an efficient training method and validate our conclusions on CIFAR-10 and CIFAR-100 matching state of the art accuracy. Remarkably, our 32 layer wider model performs similar to a 1001 layer ResNet model.
|
[link]
* They describe a regularization method similar to dropout and stochastic depth.
* The method could be viewed as a merge of the two techniques (dropout, stochastic depth).
* The method seems to regularize better than any of the two alone.
### How
* Let `x` be the input to a layer. That layer produces an output. The output can be:
* Feed forward ("classic") network: `F(x)`.
* Residual network: `x + F(x)`.
* The standard dropout-like methods do the following:
* Dropout in feed forward networks: Sometimes `0`, sometimes `F(x)`. Decided per unit.
* Dropout in residual networks (rarely used): Sometimes `0`, sometimes `x + F(x)`. Decided per unit.
* Stochastic depth (only in residual networks): Sometimes `x`, sometimes `x + F(x)`. Decided per *layer*.
* Skip forward (only in residual networks): Sometimes `x`, sometimes `x + F(x)`. Decided per unit.
* **Swapout** (any network): Sometimes `0`, sometimes `F(x)`, sometimes `x`, sometimes `x + F(x)`. Decided per unit.
* Swapout can be represented using the formula `y = theta_1 * x + theta_2 * F(x)`.
* `*` is the element-wise product.
* `theta_1` and `theta_2` are tensors following bernoulli distributions, i.e. their values are all exactly `0` or exactly `1`.
* Setting the values of `theta_1` and `theta_2` per unit in the right way leads to the values `0` (both 0), `x` (1, 0), `F(x)` (0, 1) or `x + F(x)` (1, 1).
* Deterministic and Stochastic Inference
* Ideally, when using a dropout-like technique you would like to get rid of its stochastic effects during prediction, so that you can predict values with exactly *one* forward pass through the network (instead of having to average over many passes).
* For Swapout it can be mathematically shown that you can't calculate a deterministic version of it that performs equally to the stochastic one (averaging over many forward passes).
* This is even more the case when using Batch Normalization in a network. (Actually also when not using Swapout, but instead Dropout + BN.)
* So for best results you should use the stochastic method (averaging over many forward passes).
### Results
* They compare various dropout-like methods, including Swapout, applied to residual networks. (On CIFAR-10 and CIFAR-100.)
* General performance:
* Results with Swapout are better than with the other methods.
* According to their results, the ranking of methods is roughly: Swapout > Dropout > Stochastic Depth > Skip Forward > None.
* Stochastic vs deterministic method:
* The stochastic method of swapout (average over N forward passes) performs significantly better than the deterministic one.
* Using about 15-30 forward passes seems to yield good results.
* Optimal parameter choice:
* Previously the Swapout-formula `y = theta_1 * x + theta_2 * F(x)` was mentioned.
* `theta_1` and `theta_2` are generated via Bernoulli distributions which have parameters `p_1` and `p_2`.
* If using fixed values for `p_1` and `p_2` throughout the network, it seems to be best to either set both of them to `0.5` or to set `p_1` to `>0.5` and `p_2` to `<0.5` (preference towards `y = x`).
* It's best however to start both at `1.0` (always `y = x + F(x)`) and to then linearly decay them to both `0.5` towards the end of the network, i.e. to apply less noise to the early layers. (This is similar to the results in the Stochastic Depth paper.)
* Thin vs. wide residual networks:
* The standard residual networks that they compared to used a `(16, 32, 64)` pattern for their layers, i.e. they started with layers of each having 16 convolutional filters, followed by some layers with each having 32 filters, followed by some layers with 64 filters.
* They tried instead a `(32, 64, 128)` pattern, i.e. they doubled the amount of filters.
* Then they reduced the number of layers from 100 down to 20.
* Their wider residual network performed significantly better than the deep and thin counterpart. However, their parameter count also increased by about `4` times.
* Increasing the pattern again to `(64, 128, 256)` and increasing the number of layers from 20 to 32 leads to another performance improvement, beating a 1000-layer network of pattern `(16, 32, 64)`. (Parameter count is then `27` times the original value.)
* Comments
* Stochastic depth works layer-wise, while Swapout works unit-wise. When a layer in Stochastic Depth is dropped, its whole forward- and backward-pass don't have to be calculated. That saves time. Swapout is not going to save time.
* They argue that dropout+BN would also profit from using stochastic inference instead of deterministic inference, just like Swapout does. However, they don't mention using it for dropout in their comparison, only for Swapout.
* They show that linear decay for their parameters (less dropping on early layers, more on later ones) significantly improves the results of Swapout. However, they don't mention testing the same thing for dropout. Maybe dropout would also profit from it?
* For the above two points: Dropout's test error is at 5.87, Swapout's test error is at 5.68. So the difference is already quite small, making any disadvantage for dropout significant.

*Visualization of how Swapout works. From left to right: An input `x`; a standard layer is applied to the input `F(x)`; a residual layer is applied to the input `x + F(x)`; Skip Forward is applied to the layer; Swapout is applied to the layer. Stochastic Depth would be all units being orange (`x`) or blue (`x + F(x)`).*
 |
Multi-Scale Context Aggregation by Dilated Convolutions
Yu, Fisher and Koltun, Vladlen
arXiv e-Print archive - 2015 via Local Bibsonomy
Keywords: dblp
Yu, Fisher and Koltun, Vladlen
arXiv e-Print archive - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe a variation of convolutions that have a differently structured receptive field. * They argue that their variation works better for dense prediction, i.e. for predicting values for every pixel in an image (e.g. coloring, segmentation, upscaling). ### How * One can image the input into a convolutional layer as a 3d-grid. Each cell is a "pixel" generated by a filter. * Normal convolutions compute their output per cell as a weighted sum of the input cells in a dense area. I.e. all input cells are right next to each other. * In dilated convolutions, the cells are not right next to each other. E.g. 2-dilated convolutions skip 1 cell between each input cell, 3-dilated convolutions skip 2 cells etc. (Similar to striding.) * Normal convolutions are simply 1-dilated convolutions (skipping 0 cells). * One can use a 1-dilated convolution and then a 2-dilated convolution. The receptive field of the second convolution will then be 7x7 instead of the usual 5x5 due to the spacing. * Increasing the dilation factor by 2 per layer (1, 2, 4, 8, ...) leads to an exponential increase in the receptive field size, while every cell in the receptive field will still be part in the computation of at least one convolution. * They had problems with badly performing networks, which they fixed using an identity initialization for the weights. (Sounds like just using resdiual connections would have been easier.)  *Receptive fields of a 1-dilated convolution (1st image), followed by a 2-dilated conv. (2nd image), followed by a 4-dilated conv. (3rd image). The blue color indicates the receptive field size (notice the exponential increase in size). Stronger blue colors mean that the value has been used in more different convolutions.* ### Results * They took a VGG net, removed the pooling layers and replaced the convolutions with dilated ones (weights can be kept). * They then used the network to segment images. * Their results were significantly better than previous methods. * They also added another network with more dilated convolutions in front of the VGG one, again improving the results.  *Their performance on a segmentation task compared to two competing methods. They only used VGG16 without pooling layers and with convolutions replaced by dilated convolutions.*  |
Texture Synthesis Through Convolutional Neural Networks and Spectrum Constraints
Liu, Gang and Gousseau, Yann and Xia, Gui-Song
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Liu, Gang and Gousseau, Yann and Xia, Gui-Song
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* The well known method of Artistic Style Transfer can be used to generate new texture images (from an existing example) by skipping the content loss and only using the style loss.
* The method however can have problems with large scale structures and quasi-periodic patterns.
* They add a new loss based on the spectrum of the images (synthesized image and style image), which decreases these problems and handles especially periodic patterns well.
### How
* Everything is handled in the same way as in the Artistic Style Transfer paper (without content loss).
* On top of that they add their spectrum loss:
* The loss is based on a squared distance, i.e. $1/2 d(I_s, I_t)^2$.
* $I_s$ is the last synthesized image.
* $I_t$ is the texture example.
* $d(I_s, I_t)$ then does the following:
* It assumes that $I_t$ is an example for a space of target images.
* Within that set it finds the image $I_p$ which is most similar to $I_s$. That is done using a projection via Fourier Transformations. (See formula 5 in the paper.)
* The returned distance is then $I_s - I_p$.
### Results
* Equal quality for textures without quasi-periodic structures.
* Significantly better quality for textures with quasi-periodic structures.
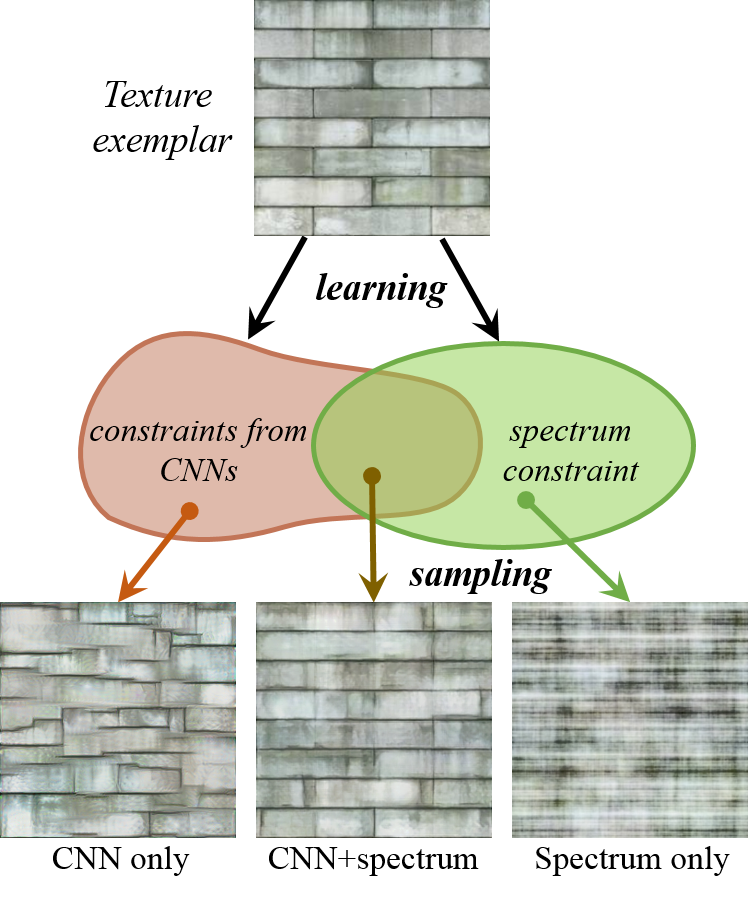
*Overview over their method, i.e. generated textures using style and/or spectrum-based loss.*
 |
Precomputed Real-Time Texture Synthesis with Markovian Generative Adversarial Networks
Li, Chuan and Wand, Michael
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
Li, Chuan and Wand, Michael
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
https://www.youtube.com/watch?v=PRD8LpPvdHI
* They describe a method that can be used for two problems:
* (1) Choose a style image and apply that style to other images.
* (2) Choose an example texture image and create new texture images that look similar.
* In contrast to previous methods their method can be applied very fast to images (style transfer) or noise (texture creation). However, per style/texture a single (expensive) initial training session is still necessary.
* Their method builds upon their previous paper "Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis".
### How
* Rough overview of their previous method:
* Transfer styles using three losses:
* Content loss: MSE between VGG representations.
* Regularization loss: Sum of x-gradient and y-gradients (encouraging smooth areas).
* MRF-based style loss: Sample `k x k` patches from VGG representations of content image and style image. For each patch from content image find the nearest neighbor (based on normalized cross correlation) from style patches. Loss is then the sum of squared errors of euclidean distances between content patches and their nearest neighbors.
* Generation of new images is done by starting with noise and then iteratively applying changes that minimize the loss function.
* They introduce mostly two major changes:
* (a) Get rid of the costly nearest neighbor search for the MRF loss. Instead, use a discriminator-network that receives a patch and rates how real that patch looks.
* This discriminator-network is costly to train, but that only has to be done once (per style/texture).
* (b) Get rid of the slow, iterative generation of images. Instead, start with the content image (style transfer) or noise image (texture generation) and feed that through a single generator-network to create the output image (with transfered style or generated texture).
* This generator-network is costly to train, but that only has to be done once (per style/texture).
* MDANs
* They implement change (a) to the standard architecture and call that an "MDAN" (Markovian Deconvolutional Adversarial Networks).
* So the architecture of the MDAN is:
* Input: Image (RGB pixels)
* Branch 1: Markovian Patch Quality Rater (aka Discriminator)
* Starts by feeding the image through VGG19 until layer `relu3_1`. (Note: VGG weights are fixed/not trained.)
* Then extracts `k x k` patches from the generated representations.
* Feeds each patch through a shallow ConvNet (convolution with BN then fully connected layer).
* Training loss is a hinge loss, i.e. max margin between classes +1 (real looking patch) and -1 (fake looking patch). (Could also take a single sigmoid output, but they argue that hinge loss isn't as likely to saturate.)
* This branch will be trained continuously while synthesizing a new image.
* Branch 2: Content Estimation/Guidance
* Note: This branch is only used for style transfer, i.e if using an content image and not for texture generation.
* Starts by feeding the currently synthesized image through VGG19 until layer `relu5_1`. (Note: VGG weights are fixed/not trained.)
* Also feeds the content image through VGG19 until layer `relu5_1`.
* Then uses a MSE loss between both representations (so similar to a MSE on RGB pixels that is often used in autoencoders).
* Nothing in this branch needs to trained, the loss only affects the synthesizing of the image.
* MGANs
* The MGAN is like the MDAN, but additionally implements change (b), i.e. they add a generator that takes an image and stylizes it.
* The generator's architecture is:
* Input: Image (RGB pixels) or noise (for texture synthesis)
* Output: Image (RGB pixels) (stylized input image or generated texture)
* The generator takes the image (pixels) and feeds that through VGG19 until layer `relu4_1`.
* Similar to the DCGAN generator, they then apply a few fractionally strided convolutions (with BN and LeakyReLUs) to that, ending in a Tanh output. (Fractionally strided convolutions increase the height/width of the images, here to compensate the VGG pooling layers.)
* The output after the Tanh is the output image (RGB pixels).
* They train the generator with pairs of `(input image, stylized image or texture)`. These pairs can be gathered by first running the MDAN alone on several images. (With significant augmentation a few dozen pairs already seem to be enough.)
* One of two possible loss functions can then be used:
* Simple standard choice: MSE on the euclidean distance between expected output pixels and generated output pixels. Can cause blurriness.
* Better choice: MSE on a higher VGG representation. Simply feed the generated output pixels through VGG19 until `relu4_1` and the reuse the already generated (see above) VGG-representation of the input image. This is very similar to the pixel-wise comparison, but tends to cause less blurriness.
* Note: For some reason the authors call their generator a VAE, but don't mention any typical VAE technique, so it's not described like one here.
* They use Adam to train their networks.
* For texture generation they use Perlin Noise instead of simple white noise. In Perlin Noise, lower frequency components dominate more than higher frequency components. White noise didn't work well with the VGG representations in the generator (activations were close to zero).
### Results
* Similar quality like previous methods, but much faster (compared to most methods).
* For the Markovian Patch Quality Rater (MDAN branch 1):
* They found that the weights of this branch can be used as initialization for other training sessions (e.g. other texture styles), leading to a decrease in required iterations/epochs.
* Using VGG for feature extraction seems to be crucial. Training from scratch generated in worse results.
* Using larger patch sizes preserves more structure of the structure of the style image/texture. Smaller patches leads to more flexibility in generated patterns.
* They found that using more than 3 convolutional layers or more than 64 filters per layer provided no visible benefit in quality.

*Result of their method, compared to other methods.*

*Architecture of their model.*
 |
Semantic Style Transfer and Turning Two-Bit Doodles into Fine Artworks
Alex J. Champandard
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/03/05 (8 years ago)
Abstract: Convolutional neural networks (CNNs) have proven highly effective at image synthesis and style transfer. For most users, however, using them as tools can be a challenging task due to their unpredictable behavior that goes against common intuitions. This paper introduces a novel concept to augment such generative architectures with semantic annotations, either by manually authoring pixel labels or using existing solutions for semantic segmentation. The result is a content-aware generative algorithm that offers meaningful control over the outcome. Thus, we increase the quality of images generated by avoiding common glitches, make the results look significantly more plausible, and extend the functional range of these algorithms---whether for portraits or landscapes, etc. Applications include semantic style transfer and turning doodles with few colors into masterful paintings!
more
less
Alex J. Champandard
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/03/05 (8 years ago)
Abstract: Convolutional neural networks (CNNs) have proven highly effective at image synthesis and style transfer. For most users, however, using them as tools can be a challenging task due to their unpredictable behavior that goes against common intuitions. This paper introduces a novel concept to augment such generative architectures with semantic annotations, either by manually authoring pixel labels or using existing solutions for semantic segmentation. The result is a content-aware generative algorithm that offers meaningful control over the outcome. Thus, we increase the quality of images generated by avoiding common glitches, make the results look significantly more plausible, and extend the functional range of these algorithms---whether for portraits or landscapes, etc. Applications include semantic style transfer and turning doodles with few colors into masterful paintings!
|
[link]
* They describe a method to transfer image styles based on semantic classes.
* This allows to:
* (1) Transfer styles between images more accurately than with previous models. E.g. so that the background of an image does not receive the style of skin/hair/clothes/... seen in the style image. Skin in the synthesized image should receive the style of skin from the style image. Same for hair, clothes, etc.
* (2) Turn simple doodles into artwork by treating the simplified areas in the doodle as semantic classes and annotating an artwork with these same semantic classes. (E.g. "this blob should receive the style from these trees.")
### How
* Their method is based on [Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis](Combining_MRFs_and_CNNs_for_Image_Synthesis.md).
* They use the same content loss and mostly the same MRF-based style loss. (Apparently they don't use the regularization loss.)
* They change the input of the MRF-based style loss.
* Usually that input would only be the activations of a VGG-layer (for the synthesized image or the style source image).
* They add a semantic map with weighting `gamma` to the activation, i.e. `<representation of image> = <activation of specific layer for that image> || gamma * <semantic map>`.
* The semantic map has N channels with 1s in a channel where a specific class is located (e.g. skin).
* The semantic map has to be created by the user for both the content image and the style image.
* As usually for the MRF loss, patches are then sampled from the representations. The semantic maps then influence the distance measure. I.e. patches are more likely to be sampled from the same semantic class.
* Higher `gamma` values make it more likely to sample from the same semantic class (because the distance from patches from different classes gets larger).
* One can create a small doodle with few colors, then use the colors as the semantic map. Then add a semantic map to an artwork and run the algorithm to transform the doodle into an artwork.
### Results
* More control over the transfered styles than previously.
* Less sensitive to the style weighting, because of the additional `gamma` hyperparameter.
* Easy transformation from doodle to artwork.

*Turning a doodle into an artwork. Note that the doodle input image is also used as the semantic map of the input.*
 |
Combining Markov Random Fields and Convolutional Neural Networks for Image Synthesis
Li, Chuan and Wand, Michael
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
Li, Chuan and Wand, Michael
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe a method that applies the style of a source image to a target image.
* Example: Let a normal photo look like a van Gogh painting.
* Example: Let a normal car look more like a specific luxury car.
* Their method builds upon the well known artistic style paper and uses a new MRF prior.
* The prior leads to locally more plausible patterns (e.g. less artifacts).
### How
* They reuse the content loss from the artistic style paper.
* The content loss was calculated by feed the source and target image through a network (here: VGG19) and then estimating the squared error of the euclidean distance between one or more hidden layer activations.
* They use layer `relu4_2` for the distance measurement.
* They replace the original style loss with a MRF based style loss.
* Step 1: Extract from the source image `k x k` sized overlapping patches.
* Step 2: Perform step (1) analogously for the target image.
* Step 3: Feed the source image patches through a pretrained network (here: VGG19) and select the representations `r_s` from specific hidden layers (here: `relu3_1`, `relu4_1`).
* Step 4: Perform step (3) analogously for the target image. (Result: `r_t`)
* Step 5: For each patch of `r_s` find the best matching patch in `r_t` (based on normalized cross correlation).
* Step 6: Calculate the sum of squared errors (based on euclidean distances) of each patch in `r_s` and its best match (according to step 5).
* They add a regularizer loss.
* The loss encourages smooth transitions in the synthesized image (i.e. few edges, corners).
* It is based on the raw pixel values of the last synthesized image.
* For each pixel in the synthesized image, they calculate the squared x-gradient and the squared y-gradient and then add both.
* They use the sum of all those values as their loss (i.e. `regularizer loss = <sum over all pixels> x-gradient^2 + y-gradient^2`).
* Their whole optimization problem is then roughly `image = argmin_image MRF-style-loss + alpha1 * content-loss + alpha2 * regularizer-loss`.
* In practice, they start their synthesis with a low resolution image and then progressively increase the resolution (each time performing some iterations of optimization).
* In practice, they sample patches from the style image under several different rotations and scalings.
### Results
* In comparison to the original artistic style paper:
* Less artifacts.
* Their method tends to preserve style better, but content worse.
* Can handle photorealistic style transfer better, so long as the images are similar enough. If no good matches between patches can be found, their method performs worse.

*Non-photorealistic example images. Their method vs. the one from the original artistic style paper.*

*Photorealistic example images. Their method vs. the one from the original artistic style paper.*
 |
Accurate Image Super-Resolution Using Very Deep Convolutional Networks
Kim, Jiwon and Lee, Jung Kwon and Lee, Kyoung Mu
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
Kim, Jiwon and Lee, Jung Kwon and Lee, Kyoung Mu
Conference and Computer Vision and Pattern Recognition - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe a model that upscales low resolution images to their high resolution equivalents ("Single Image Super Resolution").
* Their model uses a deeper architecture than previous models and has a residual component.
### How
* Their model is a fully convolutional neural network.
* Input of the model: The image to upscale, *already upscaled to the desired size* (but still blurry).
* Output of the model: The upscaled image (without the blurriness).
* They use 20 layers of padded 3x3 convolutions with size 64xHxW with ReLU activations. (No pooling.)
* They have a residual component, i.e. the model only learns and outputs the *change* that has to be applied/added to the blurry input image (instead of outputting the full image). That change is applied to the blurry input image before using the loss function on it. (Note that this is a bit different from the currently used "residual learning".)
* They use a MSE between the "correct" upscaling and the generated upscaled image (input image + residual).
* They use SGD starting with a learning rate of 0.1 and decay it 3 times by a factor of 10.
* They use weight decay of 0.0001.
* During training they use a special gradient clipping adapted to the learning rate. Usually gradient clipping restricts the gradient values to `[-t, t]` (`t` is a hyperparameter). Their gradient clipping restricts the values to `[-t/lr, t/lr]` (where `lr` is the learning rate).
* They argue that their special gradient clipping allows the use of significantly higher learning rates.
* They train their model on multiple scales, e.g. 2x, 3x, 4x upscaling. (Not really clear how. They probably feed their upscaled image again into the network or something like that?)
### Results
* Higher accuracy upscaling than all previous methods.
* Can handle well upscaling factors above 2x.
* Residual network learns significantly faster than non-residual network.

*Architecture of the model.*

*Super-resolution quality of their model (top, bottom is a competing model).*
 |
Joint Training of a Convolutional Network and a Graphical Model for Human Pose Estimation
Tompson, Jonathan J. and Jain, Arjun and LeCun, Yann and Bregler, Christoph
Neural Information Processing Systems Conference - 2014 via Local Bibsonomy
Keywords: dblp
Tompson, Jonathan J. and Jain, Arjun and LeCun, Yann and Bregler, Christoph
Neural Information Processing Systems Conference - 2014 via Local Bibsonomy
Keywords: dblp
|
[link]
* They describe a model for human pose estimation, i.e. one that finds the joints ("skeleton") of a person in an image.
* They argue that part of their model resembles a Markov Random Field (but in reality its implemented as just one big neural network).
### How
* They have two components in their network:
* Part-Detector:
* Finds candidate locations for human joints in an image.
* Pretty standard ConvNet. A few convolutional layers with pooling and ReLUs.
* They use two branches: A fine and a coarse one. Both branches have practically the same architecture (convolutions, pooling etc.). The coarse one however receives the image downscaled by a factor of 2 (half width/height) and upscales it by a factor of 2 at the end of the branch.
* At the end they merge the results of both branches with more convolutions.
* The output of this model are 4 heatmaps (one per joint? unclear), each having lower resolution than the original image.
* Spatial-Model:
* Takes the results of the part detector and tries to remove all detections that were false positives.
* They derive their architecture from a fully connected Markov Random Field which would be solved with one step of belief propagation.
* They use large convolutions (128x128) to resemble the "fully connected" part.
* They initialize the weights of the convolutions with joint positions gathered from the training set.
* The convolutions are followed by log(), element-wise additions and exp() to resemble an energy function.
* The end result are the input heatmaps, but cleaned up.
### Results
* Beats all previous models (with and without spatial model).
* Accuracy seems to be around 90% (with enough (16px) tolerance in pixel distance from ground truth).
* Adding the spatial model adds a few percentage points of accuracy.
* Using two branches instead of one (in the part detector) adds a bit of accuracy. Adding a third branch adds a tiny bit more.
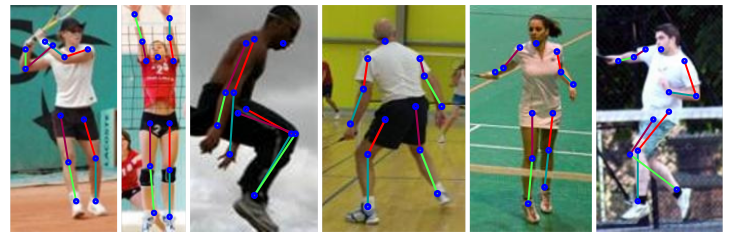
*Example results.*
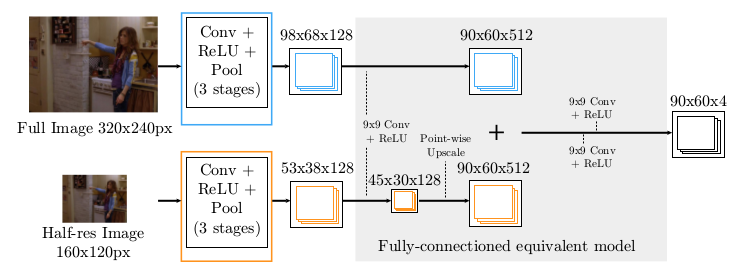
*Part Detector network.*
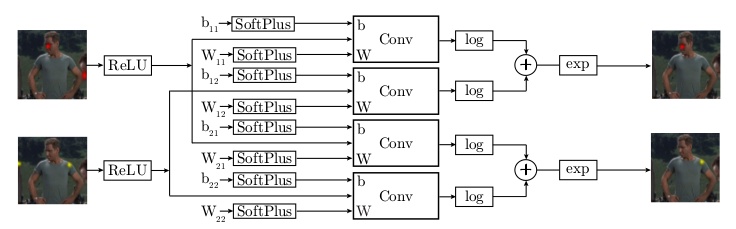
*Spatial Model (apparently only for two input heatmaps).*
-------------------------
# Rough chapter-wise notes
* (1) Introduction
* Human Pose Estimation (HPE) from RGB images is difficult due to the high dimensionality of the input.
* Approaches:
* Deformable-part models: Traditionally based on hand-crafted features.
* Deep-learning based disciminative models: Recently outperformed other models. However, it is hard to incorporate priors (e.g. possible joint- inter-connectivity) into the model.
* They combine:
* A part-detector (ConvNet, utilizes multi-resolution feature representation with overlapping receptive fields)
* Part-based Spatial-Model (approximates loopy belief propagation)
* They backpropagate through the spatial model and then the part-detector.
* (3) Model
* (3.1) Convolutional Network Part-Detector
* This model locates possible positions of human key joints in the image ("part detector").
* Input: RGB image.
* Output: 4 heatmaps, one per key joint (per pixel: likelihood).
* They use a fully convolutional network.
* They argue that applying convolutions to every pixel is similar to moving a sliding window over the image.
* They use two receptive field sizes for their "sliding window": A large but coarse/blurry one, a small but fine one.
* To implement that, they use two branches. Both branches are mostly identical (convolutions, poolings, ReLU). They simply feed a downscaled (half width/height) version of the input image into the coarser branch. At the end they upscale the coarser branch once and then merge both branches.
* After the merge they apply 9x9 convolutions and then 1x1 convolutions to get it down to 4xHxW (H=60, W=90 where expected input was H=320, W=240).
* (3.2) Higher-level Spatial-Model
* This model takes the detected joint positions (heatmaps) and tries to remove those that are probably false positives.
* It is a ConvNet, which tries to emulate (1) a Markov Random Field and (2) solving that MRF approximately via one step of belief propagation.
* The raw MRF formula would be something like `<likelihood of joint A per px> = normalize( <product over joint v from joints V> <probability of joint A per px given a> * <probability of joint v at px?> + someBiasTerm)`.
* They treat the probabilities as energies and remove from the formula the partition function (`normalize`) for various reasons (e.g. because they are only interested in the maximum value anyways).
* They use exp() in combination with log() to replace the product with a sum.
* They apply SoftPlus and ReLU so that the energies are always positive (and therefore play well with log).
* Apparently `<probability of joint v at px?>` are the input heatmaps of the part detector.
* Apparently `<probability of joint A per px given a>` is implemented as the weights of a convolution.
* Apparently `someBiasTerm` is implemented as the bias of a convolution.
* The convolutions that they use are large (128x128) to emulate a fully connected graph.
* They initialize the convolution weights based on histograms gathered from the dataset (empirical distribution of joint displacements).
* (3.3) Unified Models
* They combine the part-based model and the spatial model to a single one.
* They first train only the part-based model, then only the spatial model, then both.
* (4) Results
* Used datasets: FLIC (4k training images, 1k test, mostly front-facing and standing poses), FLIC-plus (17k, 1k ?), extended-LSP (10k, 1k).
* FLIC contains images showing multiple persons with only one being annotated. So for FLIC they add a heatmap of the annotated body torso to the input (i.e. the part-detector does not have to search for the person any more).
* The evaluation metric roughly measures, how often predicted joint positions are within a certain radius of the true joint positions.
* Their model performs significantly better than competing models (on both FLIC and LSP).
* Accuracy seems to be at around 80%-95% per joint (when choosing high enough evaluation tolerance, i.e. 10px+).
* Adding the spatial model to the part detector increases the accuracy by around 10-15 percentage points.
* Training the part detector and the spatial model jointly adds ~3 percentage points accuracy over training them separately.
* Adding the second filter bank (coarser branch in the part detector) adds around 5 percentage points accuracy. Adding a third filter bank adds a tiny bit more accuracy.
 |
Hierarchical Deep Reinforcement Learning: Integrating Temporal Abstraction and Intrinsic Motivation
Tejas D. Kulkarni and Karthik R. Narasimhan and Ardavan Saeedi and Joshua B. Tenenbaum
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.AI, cs.CV, cs.NE, stat.ML
First published: 2016/04/20 (7 years ago)
Abstract: Learning goal-directed behavior in environments with sparse feedback is a major challenge for reinforcement learning algorithms. The primary difficulty arises due to insufficient exploration, resulting in an agent being unable to learn robust value functions. Intrinsically motivated agents can explore new behavior for its own sake rather than to directly solve problems. Such intrinsic behaviors could eventually help the agent solve tasks posed by the environment. We present hierarchical-DQN (h-DQN), a framework to integrate hierarchical value functions, operating at different temporal scales, with intrinsically motivated deep reinforcement learning. A top-level value function learns a policy over intrinsic goals, and a lower-level function learns a policy over atomic actions to satisfy the given goals. h-DQN allows for flexible goal specifications, such as functions over entities and relations. This provides an efficient space for exploration in complicated environments. We demonstrate the strength of our approach on two problems with very sparse, delayed feedback: (1) a complex discrete stochastic decision process, and (2) the classic ATARI game `Montezuma's Revenge'.
more
less
Tejas D. Kulkarni and Karthik R. Narasimhan and Ardavan Saeedi and Joshua B. Tenenbaum
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.AI, cs.CV, cs.NE, stat.ML
First published: 2016/04/20 (7 years ago)
Abstract: Learning goal-directed behavior in environments with sparse feedback is a major challenge for reinforcement learning algorithms. The primary difficulty arises due to insufficient exploration, resulting in an agent being unable to learn robust value functions. Intrinsically motivated agents can explore new behavior for its own sake rather than to directly solve problems. Such intrinsic behaviors could eventually help the agent solve tasks posed by the environment. We present hierarchical-DQN (h-DQN), a framework to integrate hierarchical value functions, operating at different temporal scales, with intrinsically motivated deep reinforcement learning. A top-level value function learns a policy over intrinsic goals, and a lower-level function learns a policy over atomic actions to satisfy the given goals. h-DQN allows for flexible goal specifications, such as functions over entities and relations. This provides an efficient space for exploration in complicated environments. We demonstrate the strength of our approach on two problems with very sparse, delayed feedback: (1) a complex discrete stochastic decision process, and (2) the classic ATARI game `Montezuma's Revenge'.
|
[link]
* They present a hierarchical method for reinforcement learning.
* The method combines "long"-term goals with short-term action choices.
### How
* They have two components:
* Meta-Controller:
* Responsible for the "long"-term goals.
* Is trained to pick goals (based on the current state) that maximize (extrinsic) rewards, just like you would usually optimize to maximize rewards by picking good actions.
* The Meta-Controller only picks goals when the Controller terminates or achieved the goal.
* Controller:
* Receives the current state and the current goal.
* Has to pick a reward maximizing action based on those, just as the agent would usually do (only the goal is added here).
* The reward is intrinsic. It comes from the Critic. The Critic gives reward whenever the current goal is reached.
* For Montezuma's Revenge:
* A goal is to reach a specific object.
* The goal is encoded via a bitmask (as big as the game screen). The mask contains 1s wherever the object is.
* They hand-extract the location of a few specific objects.
* So basically:
* The Meta-Controller picks the next object to reach via a Q-value function.
* It receives extrinsic reward when objects have been reached in a specific sequence.
* The Controller picks actions that lead to reaching the object based on a Q-value function. It iterates action-choosing until it terminates or reached the goal-object.
* The Critic awards intrinsic reward to the Controller whenever the goal-object was reached.
* They use CNNs for the Meta-Controller and the Controller, similar in architecture to the Atari-DQN paper (shallow CNNs).
* They use two replay memories, one for the Meta-Controller (size 40k) and one for the Controller (size 1M).
* Both follow an epsilon-greedy policy (for picking goals/actions). Epsilon starts at 1.0 and is annealed down to 0.1.
* They use a discount factor / gamma of 0.9.
* They train with SGD.
### Results
* Learns to play Montezuma's Revenge.
* Learns to act well in a more abstract MDP with delayed rewards and where simple Q-learning failed.
--------------------
# Rough chapter-wise notes
* (1) Introduction
* Basic problem: Learn goal directed behaviour from sparse feedbacks.
* Challenges:
* Explore state space efficiently
* Create multiple levels of spatio-temporal abstractions
* Their method: Combines deep reinforcement learning with hierarchical value functions.
* Their agent is motivated to solve specific intrinsic goals.
* Goals are defined in the space of entities and relations, which constraints the search space.
* They define their value function as V(s, g) where s is the state and g is a goal.
* First, their agent learns to solve intrinsically generated goals. Then it learns to chain these goals together.
* Their model has two hiearchy levels:
* Meta-Controller: Selects the current goal based on the current state.
* Controller: Takes state s and goal g, then selects a good action based on s and g. The controller operates until g is achieved, then the meta-controller picks the next goal.
* Meta-Controller gets extrinsic rewards, controller gets intrinsic rewards.
* They use SGD to optimize the whole system (with respect to reward maximization).
* (3) Model
* Basic setting: Action a out of all actions A, state s out of S, transition function T(s,a)->s', reward by state F(s)->R.
* epsilon-greedy is good for local exploration, but it's not good at exploring very different areas of the state space.
* They use intrinsically motivated goals to better explore the state space.
* Sequences of goals are arranged to maximize the received extrinsic reward.
* The agent learns one policy per goal.
* Meta-Controller: Receives current state, chooses goal.
* Controller: Receives current state and current goal, chooses action. Keeps choosing actions until goal is achieved or a terminal state is reached. Has the optimization target of maximizing cumulative reward.
* Critic: Checks if current goal is achieved and if so provides intrinsic reward.
* They use deep Q learning to train their model.
* There are two Q-value functions. One for the controller and one for the meta-controller.
* Both formulas are extended by the last chosen goal g.
* The Q-value function of the meta-controller does not depend on the chosen action.
* The Q-value function of the controller receives only intrinsic direct reward, not extrinsic direct reward.
* Both Q-value functions are reprsented with DQNs.
* Both are optimized to minimize MSE losses.
* They use separate replay memories for the controller and meta-controller.
* A memory is added for the meta-controller whenever the controller terminates.
* Each new goal is picked by the meta-controller epsilon-greedy (based on the current state).
* The controller picks actions epsilon-greedy (based on the current state and goal).
* Both epsilons are annealed down.
* (4) Experiments
* (4.1) Discrete MDP with delayed rewards
* Basic MDP setting, following roughly: Several states (s1 to s6) organized in a chain. The agent can move left or right. It gets high reward if it moves to state s6 and then back to s1, otherwise it gets small reward per reached state.
* They use their hierarchical method, but without neural nets.
* Baseline is Q-learning without a hierarchy/intrinsic rewards.
* Their method performs significantly better than the baseline.
* (4.2) ATARI game with delayed rewards
* They play Montezuma's Revenge with their method, because that game has very delayed rewards.
* They use CNNs for the controller and meta-controller (architecture similar to the Atari-DQN paper).
* The critic reacts to (entity1, relation, entity2) relationships. The entities are just objects visible in the game. The relation is (apparently ?) always "reached", i.e. whether object1 arrived at object2.
* They extract the objects manually, i.e. assume the existance of a perfect unsupervised object detector.
* They encode the goals apparently not as vectors, but instead just use a bitmask (game screen heightand width), which has 1s at the pixels that show the object.
* Replay memory sizes: 1M for controller, 50k for meta-controller.
* gamma=0.99
* They first only train the controller (i.e. meta-controller completely random) and only then train both jointly.
* Their method successfully learns to perform actions which lead to rewards with long delays.
* It starts with easier goals and then learns harder goals.
 |
Let there be Color!: Joint End-to-end Learning of Global and Local Image Priors for Automatic Image Colorization with Simultaneous Classification
Satoshi Iizuka and Edgar Simo-Serra and Hiroshi Ishikawa
ACM Transactions on Graphics (Proc. of SIGGRAPH 2016) - 2016 via Local
Keywords:
Satoshi Iizuka and Edgar Simo-Serra and Hiroshi Ishikawa
ACM Transactions on Graphics (Proc. of SIGGRAPH 2016) - 2016 via Local
Keywords:
|
[link]
* They present a model which adds color to grayscale images (e.g. to old black and white images).
* It works best with 224x224 images, but can handle other sizes too.
### How
* Their model has three feature extraction components:
* Low level features:
* Receives 1xHxW images and outputs 512xH/8xW/8 matrices.
* Uses 6 convolutional layers (3x3, strided, ReLU) for that.
* Global features:
* Receives the low level features and converts them to 256 dimensional vectors.
* Uses 4 convolutional layers (3x3, strided, ReLU) and 3 fully connected layers (1024 -> 512 -> 256; ReLU) for that.
* Mid-level features:
* Receives the low level features and converts them to 256xH/8xW/8 matrices.
* Uses 2 convolutional layers (3x3, ReLU) for that.
* The global and mid-level features are then merged with a Fusion Layer.
* The Fusion Layer is basically an extended convolutional layer.
* It takes the mid-level features (256xH/8xW/8) and the global features (256) as input and outputs a matrix of shape 256xH/8xW/8.
* It mostly operates like a normal convolutional layer on the mid-level features. However, its weight matrix is extended to also include weights for the global features (which will be added at every pixel).
* So they use something like `fusion at pixel u,v = sigmoid(bias + weights * [global features, mid-level features at pixel u,v])` - and that with 256 different weight matrices and biases for 256 filters.
* After the Fusion Layer they use another network to create the coloring:
* This network receives 256xH/8xW/8 matrices (merge of global and mid-level features) and generates 2xHxW outputs (color in L\*a\*b\* color space).
* It uses a few convolutional layers combined with layers that do nearest neighbour upsampling.
* The loss for the colorization network is a MSE based on the true coloring.
* They train the global feature extraction also on the true class labels of the used images.
* Their model can handle any sized image. If the image doesn't have a size of 224x224, it must be resized to 224x224 for the gobal feature extraction. The mid-level feature extraction only uses convolutions, therefore it can work with any image size.
### Results
* The training set that they use is the "Places scene dataset".
* After cleanup the dataset contains 2.3M training images (205 different classes) and 19k validation images.
* Users rate images colored by their method in 92.6% of all cases as real-looking (ground truth: 97.2%).
* If they exclude global features from their method, they only achieve 70% real-looking images.
* They can also extract the global features from image A and then use them on image B. That transfers the style from A to B. But it only works well on semantically similar images.
*Architecture of their model.*

*Their model applied to old images.*
--------------------
# Rough chapter-wise notes
* (1) Introduction
* They use a CNN to color images.
* Their network extracts global priors and local features from grayscale images.
* Global priors:
* Extracted from the whole image (e.g. time of day, indoor or outdoors, ...).
* They use class labels of images to train those. (Not needed during test.)
* Local features: Extracted from small patches (e.g. texture).
* They don't generate a full RGB image, instead they generate the chrominance map using the CIE L\*a\*b\* colorspace.
* Components of the model:
* Low level features network: Generated first.
* Mid level features network: Generated based on the low level features.
* Global features network: Generated based on the low level features.
* Colorization network: Receives mid level and global features, which were merged in a fusion layer.
* Their network can process images of arbitrary size.
* Global features can be generated based on another image to change the style of colorization, e.g. to change the seasonal colors from spring to summer.
* (3) Joint Global and Local Model
* <repetition of parts of the introduction>
* They mostly use ReLUs.
* (3.1) Deep Networks
* <standard neural net introduction>
* (3.2) Fusing Global and Local Features for Colorization
* Global features are used as priors for local features.
* (3.2.1) Shared Low-Level Features
* The low level features are which's (low level) features are fed into the networks of both the global and the medium level features extractors.
* They generate them from the input image using a ConvNet with 6 layers (3x3, 1x1 padding, strided/no pooling, ends in 512xH/8xW/8).
* (3.2.2) Global Image Features
* They process the low level features via another network into global features.
* That network has 4 conv-layers (3x3, 2 strided layers, all 512 filters), followed by 3 fully connected layers (1024, 512, 256).
* Input size (of low level features) is expected to be 224x224.
* (3.2.3) Mid-Level Features
* Takes the low level features (512xH/8xW/8) and uses 2 conv layers (3x3) to transform them to 256xH/8xW/8.
* (3.2.4) Fusing Global and Local Features
* The Fusion Layer is basically an extended convolutional layer.
* It takes the mid-level features (256xH/8xW/8) and the global features (256) as input and outputs a matrix of shape 256xH/8xW/8.
* It mostly operates like a normal convolutional layer on the mid-level features. However, its weight matrix is extended to also include weights for the global features (which will be added at every pixel).
* So they use something like `fusion at pixel u,v = sigmoid(bias + weights * [global features, mid-level features at pixel u,v])` - and that with 256 different weight matrices and biases for 256 filters.
* (3.2.5) Colorization Network
* The colorization network receives the 256xH/8xW/8 matrix from the fusion layer and transforms it to the 2xHxW chrominance map.
* It basically uses two upsampling blocks, each starting with a nearest neighbour upsampling layer, followed by 2 3x3 convs.
* The last layer uses a sigmoid activation.
* The network ends in a MSE.
* (3.3) Colorization with Classification
* To make training more effective, they train parts of the global features network via image class labels.
* I.e. they take the output of the 2nd fully connected layer (at the end of the global network), add one small hidden layer after it, followed by a sigmoid output layer (size equals number of class labels).
* They train that with cross entropy. So their global loss becomes something like `L = MSE(color accuracy) + alpha*CrossEntropy(class labels accuracy)`.
* (3.4) Optimization and Learning
* Low level feature extraction uses only convs, so they can be extracted from any image size.
* Global feature extraction uses fc layers, so they can only be extracted from 224x224 images.
* If an image has a size unequal to 224x224, it must be (1) resized to 224x224, fed through low level feature extraction, then fed through the global feature extraction and (2) separately (without resize) fed through the low level feature extraction and then fed through the mid-level feature extraction.
* However, they only trained on 224x224 images (for efficiency).
* Augmentation: 224x224 crops from 256x256 images; random horizontal flips.
* They use Adadelta, because they don't want to set learning rates. (Why not adagrad/adam/...?)
* (4) Experimental Results and Discussion
* They set the alpha in their loss to `1/300`.
* They use the "Places scene dataset". They filter images with low color variance (including grayscale images). They end up with 2.3M training images and 19k validation images. They have 205 classes.
* Batch size: 128.
* They train for about 11 epochs.
* (4.1) Colorization results
* Good looking colorization results on the Places scene dataset.
* (4.2) Comparison with State of the Art
* Their method succeeds where other methods fail.
* Their method can handle very different kinds of images.
* (4.3) User study
* When rated by users, 92.6% think that their coloring is real (ground truth: 97.2%).
* Note: Users were told to only look briefly at the images.
* (4.4) Importance of Global Features
* Their model *without* global features only achieves 70% user rating.
* There are too many ambiguities on the local level.
* (4.5) Style Transfer through Global Features
* They can perform style transfer by extracting the global features of image B and using them for image A.
* (4.6) Colorizing the past
* Their model performs well on old images despite the artifacts commonly found on those.
* (4.7) Classification Results
* Their method achieves nearly as high classification accuracy as VGG (see classification loss for global features).
* (4.8) Comparison of Color Spaces
* L\*a\*b\* color space performs slightly better than RGB and YUV, so they picked that color space.
* (4.9) Computation Time
* One image is usually processed within seconds.
* CPU takes roughly 5x longer.
* (4.10) Limitations and Discussion
* Their approach is data driven, i.e. can only deal well with types of images that appeared in the dataset.
* Style transfer works only really well for semantically similar images.
* Style transfer cannot necessarily transfer specific colors, because the whole model only sees the grayscale version of the image.
* Their model tends to strongly prefer the most common color for objects (e.g. grass always green).
 |
Artistic style transfer for videos
Manuel Ruder and Alexey Dosovitskiy and Thomas Brox
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/04/28 (7 years ago)
Abstract: In the past, manually re-drawing an image in a certain artistic style required a professional artist and a long time. Doing this for a video sequence single-handed was beyond imagination. Nowadays computers provide new possibilities. We present an approach that transfers the style from one image (for example, a painting) to a whole video sequence. We make use of recent advances in style transfer in still images and propose new initializations and loss functions applicable to videos. This allows us to generate consistent and stable stylized video sequences, even in cases with large motion and strong occlusion. We show that the proposed method clearly outperforms simpler baselines both qualitatively and quantitatively.
more
less
Manuel Ruder and Alexey Dosovitskiy and Thomas Brox
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.CV
First published: 2016/04/28 (7 years ago)
Abstract: In the past, manually re-drawing an image in a certain artistic style required a professional artist and a long time. Doing this for a video sequence single-handed was beyond imagination. Nowadays computers provide new possibilities. We present an approach that transfers the style from one image (for example, a painting) to a whole video sequence. We make use of recent advances in style transfer in still images and propose new initializations and loss functions applicable to videos. This allows us to generate consistent and stable stylized video sequences, even in cases with large motion and strong occlusion. We show that the proposed method clearly outperforms simpler baselines both qualitatively and quantitatively.
|
[link]
https://www.youtube.com/watch?v=vQk_Sfl7kSc&feature=youtu.be
* The paper describes a method to transfer the style (e.g. choice of colors, structure of brush strokes) of an image to a whole video.
* The method is designed so that the transfered style is consistent over many frames.
* Examples for such consistency:
* No flickering of style between frames. So the next frame has always roughly the same style in the same locations.
* No artefacts at the boundaries of objects, even if they are moving.
* If an area gets occluded and then unoccluded a few frames later, the style of that area is still the same as before the occlusion.
### How
* Assume that we have a frame to stylize $x$ and an image from which to extract the style $a$.
* The basic process is the same as in the original Artistic Style Transfer paper, they just add a bit on top of that.
* They start with a gaussian noise image $x'$ and change it gradually so that a loss function gets minimized.
* The loss function has the following components:
* Content loss *(old, same as in the Artistic Style Transfer paper)*
* This loss makes sure that the content in the generated/stylized image still matches the content of the original image.
* $x$ and $x'$ are fed forward through a pretrained network (VGG in their case).
* Then the generated representations of the intermediate layers of the network are extracted/read.
* One or more layers are picked and the difference between those layers for $x$ and $x'$ is measured via a MSE.
* E.g. if we used only the representations of the layer conv5 then we would get something like `(conv5(x) - conv5(x'))^2` per example. (Where conv5() also executes all previous layers.)
* Style loss *(old)*
* This loss makes sure that the style of the generated/stylized image matches the style source $a$.
* $x'$ and $a$ are fed forward through a pretrained network (VGG in their case).
* Then the generated representations of the intermediate layers of the network are extracted/read.
* One or more layers are picked and the Gram Matrices of those layers are calculated.
* Then the difference between those matrices is measured via a MSE.
* Temporal loss *(new)*
* This loss enforces consistency in style between a pair of frames.
* The main sources of inconsistency are boundaries of moving objects and areas that get unonccluded.
* They use the optical flow to detect motion.
* Applying an optical flow method to two frames $(i, i+1)$ returns per pixel the movement of that pixel, i.e. if the pixel at $(x=1, y=2)$ moved to $(x=2, y=4)$ the optical flow at that pixel would be $(u=1, v=2)$.
* The optical flow can be split into the forward flow (here `fw`) and the backward flow (here `bw`). The forward flow is the flow from frame i to i+1 (as described in the previous point). The backward flow is the flow from frame $i+1$ to $i$ (reverse direction in time).
* Boundaries
* At boundaries of objects the derivative of the flow is high, i.e. the flow "suddenly" changes significantly from one pixel to the other.
* So to detect boundaries they use (per pixel) roughly the equation `gradient(u)^2 + gradient(v)^2 > length((u,v))`.
* Occlusions and disocclusions
* If a pixel does not get occluded/disoccluded between frames, the optical flow method should be able to correctly estimate the motion of that pixel between the frames. The forward and backward flows then should be roughly equal, just in opposing directions.
* If a pixel does get occluded/disoccluded between frames, it will not be visible in one the two frames and therefore the optical flow method cannot reliably estimate the motion for that pixel. It is then expected that the forward and backward flow are unequal.
* To measure that effect they roughly use (per pixel) a formula matching `length(fw + bw)^2 > length(fw)^2 + length(bw)^2`.
* Mask $c$
* They create a mask $c$ with the size of the frame.
* For every pixel they estimate whether the boundary-equation *or* the disocclusion-equation is true.
* If either of them is true, they add a 0 to the mask, otherwise a 1. So the mask is 1 wherever there is *no* disocclusion or motion boundary.
* Combination
* The final temporal loss is the mean (over all pixels) of $c*(x-w)^2$.
* $x$ is the frame to stylize.
* $w$ is the previous *stylized* frame (frame i-1), warped according to the optical flow between frame i-1 and i.
* `c` is the mask value at the pixel.
* By using the difference `x-w` they ensure that the difference in styles between two frames is low.
* By adding `c` they ensure the style-consistency only at pixels that probably should have a consistent style.
* Long-term loss *(new)*
* This loss enforces consistency in style between pairs of frames that are longer apart from each other.
* It is a simple extension of the temporal (short-term) loss.
* The temporal loss was computed for frames (i-1, i). The long-term loss is the sum of the temporal losses for the frame pairs {(i-4,i), (i-2,i), (i-1,i)}.
* The $c$ mask is recomputed for every pair and 1 if there are no boundaries/disocclusions detected, but only if there is not a 1 for the same pixel in a later mask. The additional condition is intended to associate pixels with their closest neighbours in time to minimize possible errors.
* Note that the long-term loss can completely replace the temporal loss as the latter one is contained in the former one.
* Multi-pass approach *(new)*
* They had problems with contrast around the boundaries of the frames.
* To combat that, they use a multi-pass method in which they seem to calculate the optical flow in multiple forward and backward passes? (Not very clear here what they do and why it would help.)
* Initialization with previous frame *(new)*
* Instead of starting at a gaussian noise image every time, they instead use the previous stylized frame.
* That immediately leads to more similarity between the frames.
 |
Playing Atari with Deep Reinforcement Learning
Volodymyr Mnih and Koray Kavukcuoglu and David Silver and Alex Graves and Ioannis Antonoglou and Daan Wierstra and Martin Riedmiller
arXiv e-Print archive - 2013 via Local arXiv
Keywords: cs.LG
First published: 2013/12/19 (10 years ago)
Abstract: We present the first deep learning model to successfully learn control policies directly from high-dimensional sensory input using reinforcement learning. The model is a convolutional neural network, trained with a variant of Q-learning, whose input is raw pixels and whose output is a value function estimating future rewards. We apply our method to seven Atari 2600 games from the Arcade Learning Environment, with no adjustment of the architecture or learning algorithm. We find that it outperforms all previous approaches on six of the games and surpasses a human expert on three of them.
more
less
Volodymyr Mnih and Koray Kavukcuoglu and David Silver and Alex Graves and Ioannis Antonoglou and Daan Wierstra and Martin Riedmiller
arXiv e-Print archive - 2013 via Local arXiv
Keywords: cs.LG
First published: 2013/12/19 (10 years ago)
Abstract: We present the first deep learning model to successfully learn control policies directly from high-dimensional sensory input using reinforcement learning. The model is a convolutional neural network, trained with a variant of Q-learning, whose input is raw pixels and whose output is a value function estimating future rewards. We apply our method to seven Atari 2600 games from the Arcade Learning Environment, with no adjustment of the architecture or learning algorithm. We find that it outperforms all previous approaches on six of the games and surpasses a human expert on three of them.
|
[link]
* They use an implementation of Q-learning (i.e. reinforcement learning) with CNNs to automatically play Atari games.
* The algorithm receives the raw pixels as its input and has to choose buttons to press as its output. No hand-engineered features are used. So the model "sees" the game and "uses" the controller, just like a human player would.
* The model achieves good results on various games, beating all previous techniques and sometimes even surpassing human players.
### How
* Deep Q Learning
* *This is yet another explanation of deep Q learning, see also [this blog post](http://www.nervanasys.com/demystifying-deep-reinforcement-learning/) for longer explanation.*
* While playing, sequences of the form (`state1`, `action1`, `reward`, `state2`) are generated.
* `state1` is the current game state. The agent only sees the pixels of that state. (Example: Screen shows enemy.)
* `action1` is an action that the agent chooses. (Example: Shoot!)
* `reward` is the direct reward received for picking `action1` in `state1`. (Example: +1 for a kill.)
* `state2` is the next game state, after the action was chosen in `state1`. (Example: Screen shows dead enemy.)
* One can pick actions at random for some time to generate lots of such tuples. That leads to a replay memory.
* Direct reward
* After playing randomly for some time, one can train a model to predict the direct reward given a screen (we don't want to use the whole state, just the pixels) and an action, i.e. `Q(screen, action) -> direct reward`.
* That function would need a forward pass for each possible action that we could take. So for e.g. 8 buttons that would be 8 forward passes. To make things more efficient, we can let the model directly predict the direct reward for each available action, e.g. for 3 buttons `Q(screen) -> (direct reward of action1, direct reward of action2, direct reward of action3)`.
* We can then sample examples from our replay memory. The input per example is the screen. The output is the reward as a tuple. E.g. if we picked button 1 of 3 in one example and received a reward of +1 then our output/label for that example would be `(1, 0, 0)`.
* We can then train the model by playing completely randomly for some time, then sample some batches and train using a mean squared error. Then play a bit less randomly, i.e. start to use the action which the network thinks would generate the highest reward. Then train again, and so on.
* Indirect reward
* Doing the previous steps, the model will learn to anticipate the *direct* reward correctly. However, we also want it to predict indirect rewards. Otherwise, the model e.g. would never learn to shoot rockets at enemies, because the reward from killing an enemy would come many frames later.
* To learn the indirect reward, one simply adds the reward value of highest reward action according to `Q(state2)` to the direct reward.
* I.e. if we have a tuple (`state1`, `action1`, `reward`, `state2`), we would not add (`state1`, `action1`, `reward`) to the replay memory, but instead (`state1`, `action1`, `reward + highestReward(Q(screen2))`). (Where `highestReward()` returns the reward of the action with the highest reward according to Q().)
* By training to predict `reward + highestReward(Q(screen2))` the network learns to anticipate the direct reward *and* the indirect reward. It takes a leap of faith to accept that this will ever converge to a good solution, but it does.
* We then add `gamma` to the equation: `reward + gamma*highestReward(Q(screen2))`. `gamma` may be set to 0.9. It is a discount factor that devalues future states, e.g. because the world is not deterministic and therefore we can't exactly predict what's going to happen. Note that Q will automatically learn to stack it, e.g. `state3` will be discounted to `gamma^2` at `state1`.
* This paper
* They use the mentioned Deep Q Learning to train their model Q.
* They use a k-th frame technique, i.e. they let the model decide upon an action at (here) every 4th frame.
* Q is implemented via a neural net. It receives 84x84x4 grayscale pixels that show the game and projects that onto the rewards of 4 to 18 actions.
* The input is HxWx4 because they actually feed the last 4 frames into the network, instead of just 1 frame. So the network knows more about what things are moving how.
* The network architecture is:
* 84x84x4 (input)
* 16 convs, 8x8, stride 4, ReLU
* 32 convs, 4x4, stride 2, ReLU
* 256 fully connected neurons, ReLU
* <N_actions> fully connected neurons, linear
* They use a replay memory of 1 million frames.
### Results
* They ran experiments on the Atari games Beam Rider, Breakout, Enduro, Pong, Qbert, Seaquest and Space Invaders.
* Same architecture and hyperparameters for all games.
* Rewards were based on score changes in the games, i.e. they used +1 (score increases) and -1 (score decreased).
* Optimizer: RMSProp, Batch Size: 32.
* Trained for 10 million examples/frames per game.
* They had no problems with instability and their average Q value per game increased smoothly.
* Their method beats all other state of the art methods.
* They managed to beat a human player in games that required not so much "long" term strategies (the less frames the better).
* Video: starts at 46:05.
https://youtu.be/dV80NAlEins?t=46m05s

*The original full algorithm, as shown in the paper.*
--------------------
### Rough chapter-wise notes
* (1) Introduction
* Problems when using neural nets in reinforcement learning (RL):
* Reward signal is often sparse, noise and delayed.
* Often assumption that data samples are independent, while they are correlated in RL.
* Data distribution can change when the algorithm learns new behaviours.
* They use Q-learning with a CNN and stochastic gradient descent.
* They use an experience replay mechanism (i.e. memory) from which they can sample previous transitions (for training).
* They apply their method to Atari 2600 games in the Arcade Learning Environment (ALE).
* They use only the visible pixels as input to the network, i.e. no manual feature extraction.
* (2) Background
* blablabla, standard deep q learning explanation
* (3) Related Work
* TD-Backgammon: "Solved" backgammon. Worked similarly to Q-learning and used a multi-layer perceptron.
* Attempts to copy TD-Backgammon to other games failed.
* Research was focused on linear function approximators as there were problems with non-linear ones diverging.
* Recently again interest in using neural nets for reinforcement learning. Some attempts to fix divergence problems with gradient temporal-difference methods.
* NFQ is a very similar method (to the one in this paper), but worked on the whole batch instead of minibatches, making it slow. It also first applied dimensionality reduction via autoencoders on the images instead of training on them end-to-end.
* HyperNEAT was applied to Atari games and evolved a neural net for each game. The networks learned to exploit design flaws.
* (4) Deep Reinforcement Learning
* They want to connect a reinforcement learning algorithm with a deep neural network, e.g. to get rid of handcrafted features.
* The network is supposes to run on the raw RGB images.
* They use experience replay, i.e. store tuples of (pixels, chosen action, received reward) in a memory and use that during training.
* They use Q-learning.
* They use an epsilon-greedy policy.
* Advantages from using experience replay instead of learning "live" during game playing:
* Experiences can be reused many times (more efficient).
* Samples are less correlated.
* Learned parameters from one batch don't determine as much the distributions of the examples in the next batch.
* They save the last N experiences and sample uniformly from them during training.
* (4.1) Preprocessing and Model Architecture
* Raw Atari images are 210x160 pixels with 128 possible colors.
* They downsample them to 110x84 pixels and then crop the 84x84 playing area out of them.
* They also convert the images to grayscale.
* They use the last 4 frames as input and stack them.
* So their network input has shape 84x84x4.
* They use one output neuron per possible action. So they can compute the Q-value (expected reward) of each action with one forward pass.
* Architecture: 84x84x4 (input) => 16 8x8 convs, stride 4, ReLU => 32 4x4 convs stride 2 ReLU => fc 256, ReLU => fc N actions, linear
* 4 to 18 actions/outputs (depends on the game).
* Aside from the outputs, the architecture is the same for all games.
* (5) Experiments
* Games that they played: Beam Rider, Breakout, Enduro, Pong, Qbert, Seaquest, Space Invaders
* They use the same architecture und hyperparameters for all games.
* They give a reward of +1 whenever the in-game score increases and -1 whenever it decreases.
* They use RMSProp.
* Mini batch size was 32.
* They train for 10 million frames/examples.
* They initialize epsilon (in their epsilon greedy strategy) to 1.0 and decrease it linearly to 0.1 at one million frames.
* They let the agent decide upon an action at every 4th in-game frame (3rd in space invaders).
* (5.1) Training and stability
* They plot the average reward und Q-value per N games to evaluate the agent's training progress,
* The average reward increases in a noisy way.
* The average Q value increases smoothly.
* They did not experience any divergence issues during their training.
* (5.2) Visualizating the Value Function
* The agent learns to predict the value function accurately, even for rather long sequences (here: ~25 frames).
* (5.3) Main Evaluation
* They compare to three other methods that use hand-engineered features and/or use the pixel data combined with significant prior knownledge.
* They mostly outperform the other methods.
* They managed to beat a human player in three games. The ones where the human won seemed to require strategies that stretched over longer time frames.
 |
Attend, Infer, Repeat: Fast Scene Understanding with Generative Models
Eslami, S. M. Ali and Heess, Nicolas and Weber, Theophane and Tassa, Yuval and Kavukcuoglu, Koray and Hinton, Geoffrey E.
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Eslami, S. M. Ali and Heess, Nicolas and Weber, Theophane and Tassa, Yuval and Kavukcuoglu, Koray and Hinton, Geoffrey E.
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* AIR (attend, infer, repeat) is a recurrent autoencoder architecture to transform images into latent representations object by object.
* As an autoencoder it is unsupervised.
* The latent representation is generated in multiple time steps.
* Each time step is intended to encode information about exactly one object in the image.
* The information encoded for each object is (mostly) a what-where information, i.e. which class the object has and where (in 2D: translation, scaling) it is shown.
* AIR has a dynamic number of time step. After encoding one object the model can decide whether it has encoded all objects or whether there is another one to encode. As a result the latent layer size is not fixed.
* AIR uses an attention mechanism during the encoding to focus on each object.
### How
* At its core, AIR is a variational autoencoder.
* It maximizes lower bounds on the error instead of using a "classic" reconstruction error (like MSE on the euclidean distance).
* It has an encoder and a decoder.
* The model uses a recurrent architecture via an LSTM.
* It (ideally) encodes/decodes one object per time step.
* Encoder
* The encoder receives the image and generates latent information for one object (what object, where it is).
* At the second timestep it receives the image, the previous timestep's latent information and the previous timestep's hidden layer. It then generates another latent information (for another object).
* And so on.
* Decoder
* The decoder receives latent information from the encoder (timestep by timestep) and treats it as a what-where information when reconstructing the images.
* It takes the what-part and uses a "normal" decoder to generate an image that shows the object.
* It takes the where-part and the generated image and feeds both into a spatial transformer, which then transforms the generated image by translating or rotating it.
* Dynamic size
* AIR makes use of a dynamically sized latent layer. It is not necessarily limited to a fixed number of time steps.
* Implementation: Instead of just letting the encoder generate what-where information, the encoder also generates a "present" information, which is 0 or 1. If it is 1, the reccurence will continue with encoding and decoding another object. Otherwise it will stop.
* Attention
* To add an attention mechanism, AIR first uses the LSTM's hidden layer to generate "where" and "present" information per object.
* It stops if the "present" information is 0.
* Otherwise it uses the "where" information to focus on the object using a spatial transformer. The object is then encoded to the "what" information.
### Results
* On a dataset of images, each containing multiple MNIST digits, AIR learns to accurately count the digits and estimate their position and scale.
* When AIR is trained on images of 0 to 2 digits and tested on images containing 3 digits it performs poorly.
* When AIR is trained on images of 0, 1 or 3 digits and tested on images containing 2 digits it performs mediocre.
* DAIR performs well on both tasks. Likely because it learns to remove each digit from the image after it has investigated it.
* When AIR is trained on 0 to 2 digits and a second network is trained (separately) to work with the generated latent layer (trained to sum the shown digits and rate whether they are shown in ascending order), then that second network reaches high accuracy with relatively few examples. That indicates usefulness for unsupervised learning.
* When AIR is trained on a dataset of handwritten characters from different alphabets, it learns to represent distinct strokes in its latent layer.
* When AIR is trained in combination with a renderer (inverse graphics), it is able to accurately recover latent parameters of rendered objects - better than supervised networks. That indicates usefulness for robots which have to interact with objects.

*AIR architecture for MNIST. Left: Decoder for two objects that are each first generated (y_att) and then fed into a Spatial Transformer (y) before being combined into an image (x). Middle: , Right: Encoder with multiple time steps that generates what-where information per object and stops when the "present" information (z_pres) is 0. Right: Combination of both for MNIST with Spatial Transformer for the attention mechanism (top left).*

*Encoder with DAIR architecture. DAIR modifies the image after every timestep (e.g. to remove objects that were already encoded).*
--------------------
### Rough chapter-wise notes
* (1) Introduction
* Assumption: Images are made up of distinct objects. These objects have visual and physical properties.
* They developed a framework for efficient inference in images (i.e. get from the image to a latent representation of the objects, i.e. inverse graphics).
* Parts of the framework: High dimensional representations (e.g. object images), interpretable latent variables (e.g. for rotation) and generative processes (to combine object images with latent variables).
* Contributions:
* A scheme for efficient variational inference in latent spaces of variable dimensionality.
* Idea: Treat inference as an iterative process, implemented via an RNN that looks at one object at a time and learns an appropriate number of inference steps. (Attend-Infer-Repeat, AIR)
* End-to-end training via amortized variational inference (continuous variables: gradient descent, discrete variables: black-box optimization).
* AIR allows to train generative models that automatically learn to decompose scenes.
* AIR allows to recover objects and their attributes from rendered 3D scenes (inverse rendering).
* (2) Approach
* Just like in VAEs, the scene interpretation is treated with a bayesian approach.
* There are latent variables `z` and images `x`.
* Images are generated via a probability distribution `p(x|z)`.
* This can be reversed via bayes rule to `p(x|z) = p(x)p(z|x) / p(z)`, which means that `p(x|z)p(z) / p(x) = p(z|x)`.
* The prior `p(z)` must be chosen and captures assumptions about the distributions of the latent variables.
* `p(x|z)` is the likelihood and represents the model that generates images from latent variables.
* They assume that there can be multiple objects in an image.
* Every object gets its own latent variables.
* A probability distribution p(x|z) then converts each object (on its own) from the latent variables to an image.
* The number of objects follows a probability distribution `p(n)`.
* For the prior and likelihood they assume two scenarios:
* 2D: Three dimensions for X, Y and scale. Additionally n dimensions for its shape.
* 3D: Dimensions for X, Y, Z, rotation, object identity/category (multinomial variable). (No scale?)
* Both 2D and 3D can be separated into latent variables for "where" and "what".
* It is assumed that the prior latent variables are independent of each other.
* (2.1) Inference
* Inference for their model is intractable, therefore they use an approximation `q(z,n|x)`, which minizes `KL(q(z,n|x)||p(z,n|x))`, i.e. KL(approximation||real) using amortized variational approximation.
* Challenges for them:
* The dimensionality of their latent variable layer is a random variable p(n) (i.e. no static size.).
* Strong symmetries.
* They implement inference via an RNN which encodes the image object by object.
* The encoded latent variables can be gaussians.
* They encode the latent layer length `n` via a vector (instead of an integer). The vector has the form of `n` ones followed by one zero.
* If the length vector is `#z` then they want to approximate `q(z,#z|x)`.
* That can apparently be decomposed into `<product> q(latent variable value i, #z is still 1 at i|x, previous latent variable values) * q(has length n|z,x)`.
* So instead of computing `#z` once, they instead compute at every time step whether there is another object in the image, which indirectly creates a chain of ones followed by a zero (the `#z` vector).
* (2.2) Learning
* The parameters theta (`p`, latent variable -> image) and phi (`q`, image -> latent variables) are jointly optimized.
* Optimization happens by maximizing a lower bound `E[log(p(x,z,n) / q(z,n|x))]` called the negative free energy.
* (2.2.1) Parameters of the model theta
* Parameters theta of log(p(x,z,n)) can easily be obtained using differentiation, so long as z and n are well approximated.
* The differentiation of the lower bound with repsect to theta can be approximated using Monte Carlo methods.
* (2.2.2) Parameters of the inference network phi
* phi are the parameters of q, i.e. of the RNN that generates z and #z in i timesteps.
* At each timestep (i.e. per object) the RNN generates three kinds of information: What (object), where (it is), whether it is present (i <= n).
* Each of these information is represented via variables. These variables can be discrete or continuous.
* When differentiating w.r.t. a continuous variable they use the reparameterization trick.
* When differentiating w.r.t. a discrete variable they use the likelihood ratio estimator.
* (3) Models and Experiments
* The RNN is implemented via an LSTM.
* DAIR
* The "normal" AIR model uses at every time step the image and the RNN's hidden layer to generate the next latent information (what object, where it is and whether it is present).
* DAIR uses that latent information to change the image at every time step and then use the difference (D) image for the next time step, i.e. DAIR can remove an object from the image after it has generated latent variables for it.
* (3.1) Multi-MNIST
* They generate a dataset of images containing multiple MNIST digits.
* Each image contains 0 to 2 digits.
* AIR is trained on the dataset.
* It learns without supervision a good attention scanning policy for the images (to "hit" all digits), to count the digits visible in the image and to use a matching number of time steps.
* During training, the model seems to first learn proper reconstruction of the digits and only then to do it with as few timesteps as possible.
* (3.1.1) Strong Generalization
* They test the generalization capabilities of AIR.
* *Extrapolation task*: They generate images with 0 to 2 digits for training, then test on images with 3 digits. The model is unable to correctly count the digits (~0% accuracy).
* *Interpolation task*: They generate images with 0, 1 or 3 digits for training, then test on images with 2 digits. The model performs OK-ish (~60% accuracy).
* DAIR performs in both cases well (~80% for extrapolation, ~95% accuracy for interpolation).
* (3.1.2) Representational Power
* They train AIR on images containing 0, 1 or 2 digits.
* Then they train a second network. That network takes the output of the first one and computes a) the sum of the digits and b) estimates whether they are shown in ascending order.
* Accuracy for both tasks is ~95%.
* The network reaches that accuracy significantly faster than a separately trained CNN (i.e. requires less labels / is more unsupervised).
* (3.2) Omniglot
* They train AIR on the Omniglot dataset (1.6k handwritten characters from 50 alphabets).
* They allow the model to use up to 4 timesteps.
* The model learns to reconstruct the images in timesteps that resemble strokes.
* (3.3) 3D Scenes
* Here, the generator p(x|z) is a 3D renderer, only q(z|x) must be approximated.
* The model has to learn to count the objects and to estimate per object its identity (class) and pose.
* They use "finite-differencing" to get gradients through the renderer and use "score function estimators" to get gradients with respect to discrete variables.
* They first test with a setup where the object count is always 1. The network learns to accurately recover the object parameters.
* A similar "normal" network has much more problems with recovering the parameters, especially rotation, because the conditional probabilities are multi-modal. The lower bound maximization strategy seems to work better in those cases.
* In a second experiment with multiple complex objects, AIR also achieves high reconstruction accuracy.
 |
Noisy Activation Functions
Gülçehre, Çaglar and Moczulski, Marcin and Denil, Misha and Bengio, Yoshua
International Conference on Machine Learning - 2016 via Local Bibsonomy
Keywords: dblp
Gülçehre, Çaglar and Moczulski, Marcin and Denil, Misha and Bengio, Yoshua
International Conference on Machine Learning - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* Certain activation functions, mainly sigmoid, tanh, hard-sigmoid and hard-tanh can saturate.
* That means that their gradient is either flat 0 after threshold values (e.g. -1 and +1) or that it approaches zero for high/low values.
* If there's no gradient, training becomes slow or stops completely.
* That's a problem, because sigmoid, tanh, hard-sigmoid and hard-tanh are still often used in some models, like LSTMs, GRUs or Neural Turing Machines.
* To fix the saturation problem, they add noise to the output of the activation functions.
* The noise increases as the unit saturates.
* Intuitively, once the unit is saturating, it will occasionally "test" an activation in the non-saturating regime to see if that output performs better.
### How
* The basic formula is: `phi(x,z) = alpha*h(x) + (1-alpha)u(x) + d(x)std(x)epsilon`
* Variables in that formula:
* Non-linear part `alpha*h(x)`:
* `alpha`: A constant hyperparameter that determines the "direction" of the noise and the slope. Values below 1.0 let the noise point away from the unsaturated regime. Values <=1.0 let it point towards the unsaturated regime (higher alpha = stronger noise).
* `h(x)`: The original activation function.
* Linear part `(1-alpha)u(x)`:
* `u(x)`: First-order Taylor expansion of h(x).
* For sigmoid: `u(x) = 0.25x + 0.5`
* For tanh: `u(x) = x`
* For hard-sigmoid: `u(x) = max(min(0.25x+0.5, 1), 0)`
* For hard-tanh: `u(x) = max(min(x, 1), -1)`
* Noise/Stochastic part `d(x)std(x)epsilon`:
* `d(x) = -sgn(x)sgn(1-alpha)`: Changes the "direction" of the noise.
* `std(x) = c(sigmoid(p*v(x))-0.5)^2 = c(sigmoid(p*(h(x)-u(x)))-0.5)^2`
* `c` is a hyperparameter that controls the scale of the standard deviation of the noise.
* `p` controls the magnitude of the noise. Due to the `sigmoid(y)-0.5` this can influence the sign. `p` is learned.
* `epsilon`: A noise creating random variable. Usually either a Gaussian or the positive half of a Gaussian (i.e. `z` or `|z|`).
* The hyperparameter `c` can be initialized at a high value and then gradually decreased over time. That would be comparable to simulated annealing.
* Noise could also be applied to the input, i.e. `h(x)` becomes `h(x + noise)`.
### Results
* They replaced sigmoid/tanh/hard-sigmoid/hard-tanh units in various experiments (without further optimizations).
* The experiments were:
* Learn to execute source code (LSTM?)
* Language model from Penntreebank (2-layer LSTM)
* Neural Machine Translation engine trained on Europarl (LSTM?)
* Image caption generation with soft attention trained on Flickr8k (LSTM)
* Counting unique integers in a sequence of integers (LSTM)
* Associative recall (Neural Turing Machine)
* Noisy activations practically always led to a small or moderate improvement in resulting accuracy/NLL/BLEU.
* In one experiment annealed noise significantly outperformed unannealed noise, even beating careful curriculum learning. (Somehow there are not more experiments about that.)
* The Neural Turing Machine learned far faster with noisy activations and also converged to a much better solution.

*Hard-tanh with noise for various alphas. Noise increases in different ways in the saturing regimes.*

*Performance during training of a Neural Turing Machine with and without noisy activation units.*
--------------------
# Rough chapter-wise notes
* (1) Introduction
* ReLU and Maxout activation functions have improved the capabilities of training deep networks.
* Previously, tanh and sigmoid were used, which were only suited for shallow networks, because they saturate, which kills the gradient.
* They suggest a different avenue: Use saturating nonlinearities, but inject noise when they start to saturate (and let the network learn how much noise is "good").
* The noise allows to train deep networks with saturating activation functions.
* Many current architectures (LSTMs, GRUs, Neural Turing Machines, ...) require "hard" decisions (yes/no). But they use "soft" activation functions to implement those, because hard functions lack gradient.
* The soft activation functions can still saturate (no more gradient) and don't match the nature of the binary decision problem. So it would be good to replace them with something better.
* They instead use hard activation functions and compensate for the lack of gradient by using noise (during training).
* Networks with hard activation functions outperform those with soft ones.
* (2) Saturating Activation Functions
* Activation Function = A function that maps a real value to a new real value and is differentiable almost everywhere.
* Right saturation = The gradient of an activation function becomes 0 if the input value goes towards infinity.
* Left saturation = The gradient of an activation function becomes 0 if the input value goes towards -infinity.
* Saturation = A activation function saturates if it right-saturates and left-saturates.
* Hard saturation = If there is a constant c for which for which the gradient becomes 0.
* Soft saturation = If there is no constant, i.e. the input value must become +/- infinity.
* Soft saturating activation functions can be converted to hard saturating ones by using a first-order Taylor expansion and then clipping the values to the required range (e.g. 0 to 1).
* A hard activating tanh is just `f(x) = x`. With clipping to [-1, 1]: `max(min(f(x), 1), -1)`.
* The gradient for hard activation functions is 0 above/below certain constants, which will make training significantly more challenging.
* hard-sigmoid, sigmoid and tanh are contractive mappings, hard-tanh for some reason only when it's greater than the threshold.
* The fixed-point for tanh is 0, for the others !=0. That can have influences on the training performance.
* (3) Annealing with Noisy Activation Functions
* Suppose that there is an activation function like hard-sigmoid or hard-tanh with additional noise (iid, mean=0, variance=std^2).
* If the noise's `std` is 0 then the activation function is the original, deterministic one.
* If the noise's `std` is very high then the derivatives and gradient become high too. The noise then "drowns" signal and the optimizer just moves randomly through the parameter space.
* Let the signal to noise ratio be `SNR = std_signal / std_noise`. So if SNR is low then noise drowns the signal and exploration is random.
* By letting SNR grow (i.e. decreaseing `std_noise`) we switch the model to fine tuning mode (less coarse exploration).
* That is similar to simulated annealing, where noise is also gradually decreased to focus on better and better regions of the parameter space.
* (4) Adding Noise when the Unit Saturate
* This approach does not always add the same noise. Instead, noise is added proportinally to the saturation magnitude. More saturation, more noise.
* That results in a clean signal in "good" regimes (non-saturation, strong gradients) and a noisy signal in "bad" regimes (saturation).
* Basic activation function with noise: `phi(x, z) = h(x) + (mu + std(x)*z)`, where `h(x)` is the saturating activation function, `mu` is the mean of the noise, `std` is the standard deviation of the noise and `z` is a random variable.
* Ideally the noise is unbiased so that the expectation values of `phi(x,z)` and `h(x)` are the same.
* `std(x)` should take higher values as h(x) enters the saturating regime.
* To calculate how "saturating" a activation function is, one can `v(x) = h(x) - u(x)`, where `u(x)` is the first-order Taylor expansion of `h(x)`.
* Empirically they found that a good choice is `std(x) = c(sigmoid(p*v(x)) - 0.5)^2` where `c` is a hyperparameter and `p` is learned.
* (4.1) Derivatives in the Saturated Regime
* For values below the threshold, the gradient of the noisy activation function is identical to the normal activation function.
* For values above the threshold, the gradient of the noisy activation function is `phi'(x,z) = std'(x)*z`. (Assuming that z is unbiased so that mu=0.)
* (4.2) Pushing Activations towards the Linear Regime
* In saturated regimes, one would like to have more of the noise point towards the unsaturated regimes than away from them (i.e. let the model try often whether the unsaturated regimes might be better).
* To achieve this they use the formula `phi(x,z) = alpha*h(x) + (1-alpha)u(x) + d(x)std(x)epsilon`
* `alpha`: A constant hyperparameter that determines the "direction" of the noise and the slope. Values below 1.0 let the noise point away from the unsaturated regime. Values <=1.0 let it point towards the unsaturated regime (higher alpha = stronger noise).
* `h(x)`: The original activation function.
* `u(x)`: First-order Taylor expansion of h(x).
* `d(x) = -sgn(x)sgn(1-alpha)`: Changes the "direction" of the noise.
* `std(x) = c(sigmoid(p*v(x))-0.5)^2 = c(sigmoid(p*(h(x)-u(x)))-0.5)^2` with `c` being a hyperparameter and `p` learned.
* `epsilon`: Either `z` or `|z|`. If `z` is a Gaussian, then `|z|` is called "half-normal" while just `z` is called "normal". Half-normal lets the noise only point towards one "direction" (towards the unsaturated regime or away from it), while normal noise lets it point in both directions (with the slope being influenced by `alpha`).
* The formula can be split into three parts:
* `alpha*h(x)`: Nonlinear part.
* `(1-alpha)u(x)`: Linear part.
* `d(x)std(x)epsilon`: Stochastic part.
* Each of these parts resembles a path along which gradient can flow through the network.
* During test time the activation function is made deterministic by using its expectation value: `E[phi(x,z)] = alpha*h(x) + (1-alpha)u(x) + d(x)std(x)E[epsilon]`.
* If `z` is half-normal then `E[epsilon] = sqrt(2/pi)`. If `z` is normal then `E[epsilon] = 0`.
* (5) Adding Noise to Input of the Function
* Noise can also be added to the input of an activation function, i.e. `h(x)` becomes `h(x + noise)`.
* The noise can either always be applied or only once the input passes a threshold.
* (6) Experimental Results
* They applied noise only during training.
* They used existing setups and just changed the activation functions to noisy ones. No further optimizations.
* `p` was initialized uniformly to [-1,1].
* Basic experiment settings:
* NAN: Normal noise applied to the outputs.
* NAH: Half-normal noise, i.e. `|z|`, i.e. noise is "directed" towards the unsaturated or satured regime.
* NANI: Normal noise applied to the *input*, i.e. `h(x+noise)`.
* NANIL: Normal noise applied to the input with learned variance.
* NANIS: Normal noise applied to the input, but only if the unit saturates (i.e. above/below thresholds).
* (6.1) Exploratory analysis
* A very simple MNIST network performed slightly better with noisy activations than without. But comparison was only to tanh and hard-tanh, not ReLU or similar.
* In an experiment with a simple GRU, NANI (noisy input) and NAN (noisy output) performed practically identical. NANIS (noisy input, only when saturated) performed significantly worse.
* (6.2) Learning to Execute
* Problem setting: Predict the output of some lines of code.
* They replaced sigmoids and tanhs with their noisy counterparts (NAH, i.e. half-normal noise on output). The model learned faster.
* (6.3) Penntreebank Experiments
* They trained a standard 2-layer LSTM language model on Penntreebank.
* Their model used noisy activations, as opposed to the usually non-noisy ones.
* They could improve upon the previously best value. Normal noise and half-normal noise performed roughly the same.
* (6.4) Neural Machine Translation Experiments
* They replaced all sigmoids and tanh units in the Neural Attention Model with noisy ones. Then they trained on the Europarl corpus.
* They improved upon the previously best score.
* (6.5) Image Caption Generation Experiments
* They train a network with soft attention to generate captions for the Flickr8k dataset.
* Using noisy activation units improved the result over normal sigmoids and tanhs.
* (6.6) Experiments with Continuation
* They build an LSTM and train it to predict how many unique integers there are in a sequence of random integers.
* Instead of using a constant value for hyperparameter `c` of the noisy activations (scale of the standard deviation of the noise), they start at `c=30` and anneal down to `c=0.5`.
* Annealed noise performed significantly better then unannealed noise.
* Noise applied to the output (NAN) significantly beat noise applied to the input (NANIL).
* In a second experiment they trained a Neural Turing Machine on the associative recall task.
* Again they used annealed noise.
* The NTM with annealed noise learned by far faster than the one without annealed noise and converged to a perfect solution.
 |
SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <1MB model size
Iandola, Forrest N. and Moskewicz, Matthew W. and Ashraf, Khalid and Han, Song and Dally, William J. and Keutzer, Kurt
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Iandola, Forrest N. and Moskewicz, Matthew W. and Ashraf, Khalid and Han, Song and Dally, William J. and Keutzer, Kurt
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* The authors train a variant of AlexNet that has significantly fewer parameters than the original network, while keeping the network's accuracy stable.
* Advantages of this:
* More efficient distributed training, because less parameters have to be transferred.
* More efficient transfer via the internet, because the model's file size is smaller.
* Possibly less memory demand in production, because fewer parameters have to be kept in memory.
### How
* They define a Fire Module. A Fire Module contains of:
* Squeeze Module: A 1x1 convolution that reduces the number of channels (e.g. from 128x32x32 to 64x32x32).
* Expand Module: A 1x1 convolution and a 3x3 convolution, both applied to the output of the Squeeze Module. Their results are concatenated.
* Using many 1x1 convolutions is advantageous, because they need less parameters than 3x3s.
* They use ReLUs, only convolutions (no fully connected layers) and Dropout (50%, before the last convolution).
* They use late maxpooling. They argue that applying pooling late - rather than early - improves accuracy while not needing more parameters.
* They try residual connections:
* One network without any residual connections (performed the worst).
* One network with residual connections based on identity functions, but only between layers of same dimensionality (performed the best).
* One network with residual connections based on identity functions and other residual connections with 1x1 convs (where dimensionality changed) (performance between the other two).
* They use pruning from Deep Compression to reduce the parameters further. Pruning simply collects the 50% of all parameters of a layer that have the lowest values and sets them to zero. That creates a sparse matrix.
### Results
* 50x parameter reduction of AlexNet (1.2M parameters before pruning, 0.4M after pruning).
* 510x file size reduction of AlexNet (from 250mb to 0.47mb) when combined with Deep Compression.
* Top-1 accuracy remained stable.
* Pruning apparently can be used safely, even after the network parameters have already been reduced significantly.
* While pruning was generally safe, they found that two of their later layers reacted quite sensitive to it. Adding parameters to these (instead of removing them) actually significantly improved accuracy.
* Generally they found 1x1 convs to react more sensitive to pruning than 3x3s. Therefore they focused pruning on 3x3 convs.
* First pruning a network, then re-adding the pruned weights (initialized with 0s) and then retraining for some time significantly improved accuracy.
* The network was rather resilient to significant channel reduction in the Squeeze Modules. Reducing to 25-50% of the original channels (e.g. 128x32x32 to 64x32x32) seemed to be a good choice.
* The network was rather resilient to removing 3x3 convs and replacing them with 1x1 convs. A ratio of 2:1 to 1:1 (1x1 to 3x3) seemed to produce good results while mostly keeping the accuracy.
* Adding some residual connections between the Fire Modules improved the accuracy.
* Adding residual connections with identity functions *and also* residual connections with 1x1 convs (where dimensionality changed) improved the accuracy, but not as much as using *only* residual connections with identity functions (i.e. it's better to keep some modules without identity functions).
--------------------
### Rough chapter-wise notes
* (1) Introduction and Motivation
* Advantages from having less parameters:
* More efficient distributed training, because less data (parameters) have to be transfered.
* Less data to transfer to clients, e.g. when a model used by some app is updated.
* FPGAs often have hardly any memory, i.e. a model has to be small to be executed.
* Target here: Find a CNN architecture with less parameters than an existing one but comparable accuracy.
* (2) Related Work
* (2.1) Model Compression
* SVD-method: Just apply SVD to the parameters of an existing model.
* Network Pruning: Replace parameters below threshold with zeros (-> sparse matrix), then retrain a bit.
* Add quantization and huffman encoding to network pruning = Deep Compression.
* (2.2) CNN Microarchitecture
* The term "CNN Microarchitecture" refers to the "organization and dimensions of the individual modules" (so an Inception module would have a complex CNN microarchitecture).
* (2.3) CNN Macroarchitecture
* CNN Macroarchitecture = "big picture" / organization of many modules in a network / general characteristics of the network, like depth
* Adding connections between modules can help (e.g. residual networks)
* (2.4) Neural Network Design Space Exploration
* Approaches for Design Space Exporation (DSE):
* Bayesian Optimization, Simulated Annealing, Randomized Search, Genetic Algorithms
* (3) SqueezeNet: preserving accuracy with few parameters
* (3.1) Architectural Design Strategies
* A conv layer with N filters applied to CxHxW input (e.g. 3x128x128 for a possible first layer) with kernel size kHxkW (e.g. 3x3) has `N*C*kH*kW` parameters.
* So one way to reduce the parameters is to decrease kH and kW, e.g. from 3x3 to 1x1 (reduces parameters by a factor of 9).
* A second way is to reduce the number of channels (C), e.g. by using 1x1 convs before the 3x3 ones.
* They think that accuracy can be improved by performing downsampling later in the network (if parameter count is kept constant).
* (3.2) The Fire Module
* The Fire Module has two components:
* Squeeze Module:
* One layer of 1x1 convs
* Expand Module:
* Concat the results of:
* One layer of 1x1 convs
* One layer of 3x3 convs
* The Squeeze Module decreases the number of input channels significantly.
* The Expand Module then increases the number of input channels again.
* (3.3) The SqueezeNet architecture
* One standalone conv, then several fire modules, then a standalone conv, then global average pooling, then softmax.
* Three late max pooling laters.
* Gradual increase of filter numbers.
* (3.3.1) Other SqueezeNet details
* ReLU activations
* Dropout before the last conv layer.
* No linear layers.
* (4) Evaluation of SqueezeNet
* Results of competing methods:
* SVD: 5x compression, 56% top-1 accuracy
* Pruning: 9x compression, 57.2% top-1 accuracy
* Deep Compression: 35x compression, ~57% top-1 accuracy
* SqueezeNet: 50x compression, ~57% top-1 accuracy
* SqueezeNet combines low parameter counts with Deep Compression.
* The accuracy does not go down because of that, i.e. apparently Deep Compression can even be applied to small models without giving up on performance.
* (5) CNN Microarchitecture Design Space Exploration
* (5.1) CNN Microarchitecture metaparameters
* blabla we test various values for this and that parameter
* (5.2) Squeeze Ratio
* In a Fire Module there is first a Squeeze Module and then an Expand Module. The Squeeze Module decreases the number of input channels to which 1x1 and 3x3 both are applied (at the same time).
* They analyzed how far you can go down with the Sqeeze Module by training multiple networks and calculating the top-5 accuracy for each of them.
* The accuracy by Squeeze Ratio (percentage of input channels kept in 1x1 squeeze, i.e. 50% = reduced by half, e.g. from 128 to 64):
* 12%: ~80% top-5 accuracy
* 25%: ~82% top-5 accuracy
* 50%: ~85% top-5 accuracy
* 75%: ~86% top-5 accuracy
* 100%: ~86% top-5 accuracy
* (5.3) Trading off 1x1 and 3x3 filters
* Similar to the Squeeze Ratio, they analyze the optimal ratio of 1x1 filters to 3x3 filters.
* E.g. 50% would mean that half of all filters in each Fire Module are 1x1 filters.
* Results:
* 01%: ~76% top-5 accuracy
* 12%: ~80% top-5 accuracy
* 25%: ~82% top-5 accuracy
* 50%: ~85% top-5 accuracy
* 75%: ~85% top-5 accuracy
* 99%: ~85% top-5 accuracy
* (6) CNN Macroarchitecture Design Space Exploration
* They compare the following networks:
* (1) Without residual connections
* (2) With residual connections between modules of same dimensionality
* (3) With residual connections between all modules (except pooling layers) using 1x1 convs (instead of identity functions) where needed
* Adding residual connections (2) improved top-1 accuracy from 57.5% to 60.4% without any new parameters.
* Adding complex residual connections (3) worsed top-1 accuracy again to 58.8%, while adding new parameters.
* (7) Model Compression Design Space Exploration
* (7.1) Sensitivity Analysis: Where to Prune or Add parameters
* They went through all layers (including each one in the Fire Modules).
* In each layer they set the 50% smallest weights to zero (pruning) and measured the effect on the top-5 accuracy.
* It turns out that doing that has basically no influence on the top-5 accuracy in most layers.
* Two layers towards the end however had significant influence (accuracy went down by 5-10%).
* Adding parameters to these layers improved top-1 accuracy from 57.5% to 59.5%.
* Generally they found 1x1 layers to be more sensitive than 3x3 layers so they pruned them less aggressively.
* (7.2) Improving Accuracy by Densifying Sparse Models
* They found that first pruning a model and then retraining it again (initializing the pruned weights to 0) leads to higher accuracy.
* They could improve top-1 accuracy by 4.3% in this way.
 |
DenseCap: Fully Convolutional Localization Networks for Dense Captioning
Justin Johnson and Andrej Karpathy and Li Fei-Fei
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.CV, cs.LG
First published: 2015/11/24 (8 years ago)
Abstract: We introduce the dense captioning task, which requires a computer vision system to both localize and describe salient regions in images in natural language. The dense captioning task generalizes object detection when the descriptions consist of a single word, and Image Captioning when one predicted region covers the full image. To address the localization and description task jointly we propose a Fully Convolutional Localization Network (FCLN) architecture that processes an image with a single, efficient forward pass, requires no external regions proposals, and can be trained end-to-end with a single round of optimization. The architecture is composed of a Convolutional Network, a novel dense localization layer, and Recurrent Neural Network language model that generates the label sequences. We evaluate our network on the Visual Genome dataset, which comprises 94,000 images and 4,100,000 region-grounded captions. We observe both speed and accuracy improvements over baselines based on current state of the art approaches in both generation and retrieval settings.
more
less
Justin Johnson and Andrej Karpathy and Li Fei-Fei
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.CV, cs.LG
First published: 2015/11/24 (8 years ago)
Abstract: We introduce the dense captioning task, which requires a computer vision system to both localize and describe salient regions in images in natural language. The dense captioning task generalizes object detection when the descriptions consist of a single word, and Image Captioning when one predicted region covers the full image. To address the localization and description task jointly we propose a Fully Convolutional Localization Network (FCLN) architecture that processes an image with a single, efficient forward pass, requires no external regions proposals, and can be trained end-to-end with a single round of optimization. The architecture is composed of a Convolutional Network, a novel dense localization layer, and Recurrent Neural Network language model that generates the label sequences. We evaluate our network on the Visual Genome dataset, which comprises 94,000 images and 4,100,000 region-grounded captions. We observe both speed and accuracy improvements over baselines based on current state of the art approaches in both generation and retrieval settings.
|
[link]
* They define four subtasks of image understanding:
* *Classification*: Assign a single label to a whole image.
* *Captioning*: Assign a sequence of words (description) to a whole image*
* *Detection*: Find objects/regions in an image and assign a single label to each one.
* *Dense Captioning*: Find objects/regions in an image and assign a sequence of words (description) to each one.
* DenseCap accomplishes the fourth task, i.e. it is a model that finds objects/regions in images and describes them with natural language.
### How
* Their model consists of four subcomponents, which run for each image in sequence:
* (1) **Convolutional Network**:
* Basically just VGG-16.
* (2) **Localization Layer**:
* This layer uses a convolutional network that has mostly the same architecture as in the "Faster R-CNN" paper.
* That ConvNet is applied to a grid of anchor points on the image.
* For each anchor point, it extracts the features generated by the VGG-Net (model 1) around that point.
* It then generates the attributes of `k` (default: 12) boxes using a shallow convolutional net. These attributes are (roughly): Height, width, center x, center y, confidence score.
* It then extracts the features of these boxes from the VGG-Net output (model 1) and uses bilinear sampling to project them onto a fixed size (height, width) for the next model. The result are the final region proposals.
* By default every image pixel is an anchor point, which results in a large number of regions. Hence, subsampling is used during training and testing.
* (3) **Recognition Network**:
* Takes a region (flattened to 1d vector) and projects it onto a vector of length 4096.
* It uses fully connected layers to do that (ReLU, dropout).
* Additionally, the network takes the 4096 vector and outputs new values for the region's position and confidence (for late fine tuning).
* The 4096 vectors of all regions are combined to a matrix that is fed into the next component (RNN).
* The intended sense of the this component seems to be to convert the "visual" features of each region to a more abstract, high-dimensional representation/description.
* (4) **RNN Language Model**:
* The take each 4096 vector and apply a fully connected layer + ReLU to it.
* Then they feed it into an LSTM, followed by a START token.
* The LSTM then generates word (as one hot vectors), which are fed back into the model for the next time step.
* This is continued until the LSTM generates an END token.
* Their full loss function has five components:
* Binary logistic loss for the confidence values generated by the localization layer.
* Binary logistic loss for the confidence values generated by the recognition layer.
* Smooth L1 loss for the region dimensions generated by the localization layer.
* Smooth L1 loss for the region dimensiosn generated by the recognition layer.
* Cross-entropy at every time-step of the language model.
* The whole model can be trained end-to-end.
* Results
* They mostly use the Visual Genome dataset.
* Their model finds lots of good regions in images.
* Their model generates good captions for each region. (Only short captions with simple language however.)
* The model seems to love colors. Like 30-50% of all captions contain a color. (Probably caused by the dataset?)
* They compare to EdgeBoxes (other method to find regions in images). Their model seems to perform better.
* Their model requires about 240ms per image (test time).
* The generated regions and captions enable one to search for specific objects in images using text queries.

*Architecture of the whole model. It starts with the VGG-Net ("CNN"), followed by the localization layer, which generates region proposals. Then the recognition network converts the regions to abstract high-dimensional representations. Then the language model ("RNN") generates the caption.*


--------------------
### Rough chapter-wise notes
* (1) Introduction
* They define four subtasks of visual scene understanding:
* Classification: Assign a single label to a whole image
* Captioning: Assign a sequence of words (description) to a whole image
* Detection: Find objects in an image and assign a single label to each one
* Dense Captioning: Find objects in an image and assign a sequence of words (description) to each one
* They developed a model for dense captioning.
* It has two three important components:
* A convoltional network for scene understanding
* A localization layer for region level predictions. It predicts regions of interest and then uses bilinear sampling to extract the activations of these regions.
* A recurrent network as the language model
* They evaluate the model on the large-scale Visual Genome dataset (94k images, 4.1M region captions).
* (3) Model
* Model architecture
* Convolutional Network
* They use VGG-16, but remove the last pooling layer.
* For an image of size W, H the output is 512xW/16xH/16.
* That output is the input into the localization layer.
* Fully Convolutional Localization Layer
* Input to this layer: Activations from the convolutional network.
* Output of this layer: Regions of interest, as fixed-sized representations.
* For B Regions:
* Coordinates of the bounding boxes (matrix of shape Bx4)
* Confidence scores (vector of length B)
* Features (matrix of shape BxCxXxY)
* Method: Faster R-CNN (pooling replaced by bilinear interpolation)
* This layer is fully differentiable.
* The localization layer predicts boxes at anchor points.
* At each anchor point it proposes `k` boxes using a small convolutional network. It assigns a confidence score and coordinates (center x, center y, height, width) to each proposal.
* For an image with size 720x540 and k=12 the model would have to predict 17,280 boxes, hence subsampling is used.
* During training they use minibatches with 256/2 positive and 256/2 negative region examples. A box counts as a positive example for a specific image if it has high overlap (intersection) with an annotated box for that image.
* During test time they use greedy non-maximum suppression (NMS) (?) to subsample the 300 most confident boxes.
* The region proposals have varying box sizes, but the output of the localization layer (which will be fed into the RNN) is ought to have fixed sizes.
* So they project each proposed region onto a fixed sized region. They use bilinear sampling for that projection, which is differentiable.
* Recognition network
* Each region is flattened to a one-dimensional vector.
* That vector is fed through 2 fully connected layers (unknown size, ReLU, dropout), ending with a 4096 neuron layer.
* The confidence score and box coordinates are also adjusted by the network during that process (fine tuning).
* RNN Language Model
* Each region is translated to a sentence.
* The region is fed into an LSTM (after a linear layer + ReLU), followed by a special START token.
* The LSTM outputs multiple words as one-hot-vectors, where each vector has the length `V+1` (i.e. vocabulary size + END token).
* Loss function is average crossentropy between output words and target words.
* During test time, words are sampled until an END tag is generated.
* Loss function
* Their full loss function has five components:
* Binary logistic loss for the confidence values generated by the localization layer.
* Binary logistic loss for the confidence values generated by the recognition layer.
* Smooth L1 loss for the region dimensions generated by the localization layer.
* Smooth L1 loss for the region dimensiosn generated by the recognition layer.
* Cross-entropy at every time-step of the language model.
* The language model term has a weight of 1.0, all other components have a weight of 0.1.
* Training an optimization
* Initialization: CNN pretrained on ImageNet, all other weights from `N(0, 0.01)`.
* SGD for the CNN (lr=?, momentum=0.9)
* Adam everywhere else (lr=1e-6, beta1=0.9, beta2=0.99)
* CNN is trained after epoch 1. CNN's first four layers are not trained.
* Batch size is 1.
* Image size is 720 on the longest side.
* They use Torch.
* 3 days of training time.
* (4) Experiments
* They use the Visual Genome Dataset (94k images, 4.1M regions with captions)
* Their total vocabulary size is 10,497 words. (Rare words in captions were replaced with `<UNK>`.)
* They throw away annotations with too many words as well as images with too few/too many regions.
* They merge heavily overlapping regions to single regions with multiple captions.
* Dense Captioning
* Dense captioning task: The model receives one image and produces a set of regions, each having a caption and a confidence score.
* Evaluation metrics
* Evaluation of the output is non-trivial.
* They compare predicted regions with regions from the annotation that have high overlap (above a threshold).
* They then compare the predicted caption with the captions having similar METEOR score (above a threshold).
* Instead of setting one threshold for each comparison they use multiple thresholds. Then they calculate the Mean Average Precision using the various pairs of thresholds.
* Baseline models
* Sources of region proposals during test time:
* GT: Ground truth boxes (i.e. found by humans).
* EB: EdgeBox (completely separate and pretrained system).
* RPN: Their localization and recognition networks trained separately on VG regions dataset (i.e. trained without the RNN language model).
* Models:
* Region RNN model: Apparently the recognition layer and the RNN language model, trained on predefined regions. (Where do these regions come from? VG training dataset?)
* Full Image RNN model: Apparently the recognition layer and the RNN language model, trained on full images from MSCOCO instead of small regions.
* FCLN on EB: Apparently the recognition layer and the RNN language model, trained on regions generated by EdgeBox (EB) (on VG dataset?).
* FCLN: Apparently their full model (trained on VG dataset?).
* Discrepancy between region and image level statistics
* When evaluating the models only on METEOR (language "quality"), the *Region RNN model* consistently outperforms the *Full Image RNN model*.
* That's probably because the *Full Image RNN model* was trained on captions of whole images, while the *Region RNN model* was trained on captions of small regions, which tend to be a bit different from full image captions.
* RPN outperforms external region proposals
* Generating region proposals via RPN basically always beats EB.
* Our model outperforms individual region description
* Their full jointly trained model (FCLN) achieves the best results.
* The full jointly trained model performs significantly better than `RPN + Region RNN model` (i.e. separately trained region proposal and region captioning networks).
* Qualitative results
* Finds plenty of good regions and generates reasonable captions for them.
* Sometimes finds the same region twice.
* Runtime evaluation
* 240ms on 720x600 image with 300 region proposals.
* 166ms on 720x600 image with 100 region proposals.
* Recognition of region proposals takes up most time.
* Generating region proposals takes up the 2nd most time.
* Generating captions for regions (RNN) takes almost no time.
* Image Retrieval using Regions and Captions
* They try to search for regions based on search queries.
* They search by letting their FCLN network or EB generate 100 region proposals per network. Then they calculate per region the probability of generating the search query as the caption. They use that probability to rank the results.
* They pick images from the VG dataset, then pick captions within those images as search query. Then they evaluate the ranking of those images for the respective search query.
* The results show that the model can learn to rank objects, object parts, people and actions as expected/desired.
* The method described can also be used to detect an arbitrary number of distinct classes in images (as opposed to the usual 10 to 1000 classes), because the classes are contained in the generated captions.
 |
Deep Networks with Stochastic Depth
Huang, Gao and Sun, Yu and Liu, Zhuang and Sedra, Daniel and Weinberger, Kilian
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: deeplearning, acreuser
Huang, Gao and Sun, Yu and Liu, Zhuang and Sedra, Daniel and Weinberger, Kilian
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: deeplearning, acreuser
|
[link]
* Stochastic Depth (SD) is a method for residual networks, which randomly removes/deactivates residual blocks during training.
* As such, it is similar to dropout.
* While dropout removes neurons, SD removes blocks (roughly the layers of a residual network).
* One can argue that dropout randomly changes the width of layers, while SD randomly changes the depth of the network.
* One can argue that using dropout is similar to training an ensemble of networks with different layer widths, while using SD is similar to training an ensemble of networks with different depths.
* Using SD has the following advantages:
* It decreases the effects of vanishing gradients, because on average the network is shallower during training (per batch), thereby increasing the gradient that reaches the early blocks.
* It increases training speed, because on average less convolutions have to be applied (due to blocks being removed).
* It has a regularizing effect, because blocks cannot easily co-adapt any more. (Similar to dropout avoiding co-adaption of neurons.)
* If using an increasing removal probability for later blocks: It spends more training time on the early (and thus most important) blocks than on the later blocks.
### How
* Normal formula for a residual block (test and train):
* `output = ReLU(f(input) + identity(input))`
* `f(x)` are usually one or two convolutions.
* Formula with SD (during training):
* `output = ReLU(b * f(input) + identity(input))`
* `b` is either exactly `1` (block survived, i.e. is not removed) or exactly `0` (block was removed).
* `b` is sampled from a bernoulli random variable that has the hyperparameter `p`.
* `p` is the survival probability of a block (i.e. chance to *not* be removed). (Note that this is the opposite of dropout, where higher values lead to more removal.)
* Formula with SD (during test):
* `output = ReLU(p * f(input) + input)`
* `p` is the average probability with which this residual block survives during training, i.e. the hyperparameter for the bernoulli variable.
* The test formula has to be changed, because the network will adapt during training to blocks being missing. Activating them all at the same time can lead to overly strong signals. This is similar to dropout, where weights also have to be changed during test.
* There are two simple schemas to set `p` per layer:
* Uniform schema: Every block gets the same `p` hyperparameter, i.e. the last block has the same chance of survival as the first block.
* Linear decay schema: Survival probability is higher for early layers and decreases towards the end.
* The formula is `p = 1 - (l/L)(1-q)`.
* `l`: Number of the block for which to set `p`.
* `L`: Total number of blocks.
* `q`: Desired survival probability of the last block (0.5 is a good value).
* For linear decay with `q=0.5` and `L` blocks, on average `(3/4)L` blocks will be trained per minibatch.
* For linear decay with `q=0.5` the average speedup will be about `1/4` (25%). If using `q=0.2` the speedup will be ~40%.
### Results
* 152 layer networks with SD outperform identical networks without SD on CIFAR-10, CIFAR-100 and SVHN.
* The improvement in test error is quite significant.
* SD seems to have a regularizing effect. Networks with SD are not overfitting where networks without SD already are.
* Even networks with >1000 layers are well trainable with SD.
* The gradients that reach the early blocks of the networks are consistently significantly higher with SD than without SD (i.e. less vanishing gradient).
* The linear decay schema consistently outperforms the uniform schema (in test error). The best value seems to be `q=0.5`, though values between 0.4 and 0.8 all seem to be good. For the uniform schema only 0.8 seems to be good.

*Performance on SVHN with 152 layer networks with SD (blue, bottom) and without SD (red, top).*
*Performance on CIFAR-10 with 1202 layer networks with SD (blue, bottom) and without SD (red, top).*
*Optimal choice of the survival probability `p_L` (in this summary `q`) for the last layer, for the uniform schema (same for all other layers) and the linear decay schema (decreasing towards `p_L`). Linear decay performs consistently better and allows for lower `p_L` values, leading to more speedup.*
--------------------
### Rough chapter-wise notes
* (1) Introduction
* Problems of deep networks:
* Vanishing Gradients: During backpropagation, gradients approach zero due to being repeatedly multiplied with small weights. Possible counter-measures: Careful initialization of weights, "hidden layer supervision" (?), batch normalization.
* Diminishing feature reuse: Aequivalent problem to vanishing gradients during forward propagation. Results of early layers are repeatedly multiplied with later layer's (randomly initialized) weights. The total result then becomes meaningless noise and doesn't have a clear/strong gradient to fix it.
* Long training time: The time of each forward-backward increases linearly with layer depth. Current 152-layer networks can take weeks to train on ImageNet.
* I.e.: Shallow networks can be trained effectively and fast, but deep networks would be much more expressive.
* During testing we want deep networks, during training we want shallow networks.
* They randomly "drop out" (i.e. remove) complete layers during training (per minibatch), resulting in shallow networks.
* Result: Lower training time *and* lower test error.
* While dropout randomly removes width from the network, stochastic depth randomly removes depth from the networks.
* While dropout can be thought of as training an ensemble of networks with different depth, stochastic depth can be thought of as training an ensemble of networks with different depth.
* Stochastic depth acts as a regularizer, similar to dropout and batch normalization. It allows deeper networks without overfitting (because 1000 layers clearly wasn't enough!).
* (2) Background
* Some previous methods to train deep networks: Greedy layer-wise training, careful initializations, batch normalization, highway connections, residual connections.
* <Standard explanation of residual networks>
* <Standard explanation of dropout>
* Dropout loses effectiveness when combined with batch normalization. Seems to have basically no benefit any more for deep residual networks with batch normalization.
* (3) Deep Networks with Stochastic Depth
* They randomly skip entire layers during training.
* To do that, they use residual connections. They select random layers and use only the identity function for these layers (instead of the full residual block of identity + convolutions + add).
* ResNet architecture: They use standard residual connections. ReLU activations, 2 convolutional layers (conv->BN->ReLU->conv->BN->add->ReLU). They use <= 64 filters per conv layer.
* While the standard formula for residual connections is `output = ReLU(f(input) + identity(input))`, their formula is `output = ReLU(b * f(input) + identity(input))` with `b` being either 0 (inactive/removed layer) or 1 (active layer), i.e. is a sample of a bernoulli random variable.
* The probabilities of the bernoulli random variables are now hyperparameters, similar to dropout.
* Note that the probability here means the probability of *survival*, i.e. high value = more survivors.
* The probabilities could be set uniformly, e.g. to 0.5 for each variable/layer.
* They can also be set with a linear decay, so that the first layer has a very high probability of survival, while the last layer has a very low probability of survival.
* Linear decay formula: `p = 1 - (l/L)(1-q)` where `l` is the current layer's number, `L` is the total number of layers, `p` is the survival probability of layer `l` and `q` is the desired survival probability of the last layer (e.g. 0.5).
* They argue that linear decay is better, as the early layer extract low level features and are therefor more important.
* The expected number of surviving layers is simply the sum of the probabilities.
* For linear decay with `q=0.5` and `L=54` (i.e. 54 residual blocks = 110 total layers) the expected number of surviving blocks is roughly `(3/4)L = (3/4)54 = 40`, i.e. on average 14 residual blocks will be removed per training batch.
* With linear decay and `q=0.5` the expected speedup of training is about 25%. `q=0.2` leads to about 40% speedup (while in one test still achieving the test error of the same network without stochastic depth).
* Depending on the `q` setting, they observe significantly lower test errors. They argue that stochastic depth has a regularizing effect (training an ensemble of many networks with different depths).
* Similar to dropout, the forward pass rule during testing must be slightly changed, because the network was trained on missing values. The residual formular during test time becomes `output = ReLU(p * f(input) + input)` where `p` is the average probability with which this residual block survives during training.
* (4) Results
* Their model architecture:
* Three chains of 18 residual blocks each, so 3*18 blocks per model.
* Number of filters per conv. layer: 16 (first chain), 32 (second chain), 64 (third chain)
* Between each block they use average pooling. Then they zero-pad the new dimensions (e.g. from 16 to 32 at the end of the first chain).
* CIFAR-10:
* Trained with SGD (momentum=0.9, dampening=0, lr=0.1 after 1st epoch, 0.01 after epoch 250, 0.001 after epoch 375).
* Weight decay/L2 of 1e-4.
* Batch size 128.
* Augmentation: Horizontal flipping, crops (4px offset).
* They achieve 5.23% error (compared to 6.41% in the original paper about residual networks).
* CIFAR-100:
* Same settings as before.
* 24.58% error with stochastic depth, 27.22% without.
* SVHN:
* The use both the hard and easy sub-datasets of images.
* They preprocess to zero-mean, unit-variance.
* Batch size 128.
* Learning rate is 0.1 (start), 0.01 (after epoch 30), 0.001 (after epoch 35).
* 1.75% error with stochastic depth, 2.01% error without.
* Network without stochastic depth starts to overfit towards the end.
* Stochastic depth with linear decay and `q=0.5` gives ~25% speedup.
* 1202-layer CIFAR-10:
* They trained a 1202-layer deep network on CIFAR-10 (previous tests: 152 layers).
* Without stochastic depth: 6.72% test error.
* With stochastic depth: 4.91% test error.
* (5) Analytic experiments
* Vanishing Gradient:
* They analyzed the gradient that reaches the first layer.
* The gradient with stochastic depth is consistently higher (throughout the epochs) than without stochastic depth.
* The difference is very significant after decreasing the learning rate.
* Hyper-parameter sensitivity:
* They evaluated with test error for different choices of the survival probability `q`.
* Linear decay schema: Values between 0.4 and 0.8 perform best. 0.5 is suggested (nearly best value, good spedup). Even 0.2 improves the test error (compared to no stochastic depth).
* Uniform schema: 0.8 performs best, other values mostly significantly worse.
* Linear decay performs consistently better than the uniform schema.
 |
Multi-view Face Detection Using Deep Convolutional Neural Networks
Farfade, Sachin Sudhakar and Saberian, Mohammad J. and Li, Li-Jia
ACM ICMR - 2015 via Local Bibsonomy
Keywords: dblp
Farfade, Sachin Sudhakar and Saberian, Mohammad J. and Li, Li-Jia
ACM ICMR - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* They propose a CNN-based approach to detect faces in a wide range of orientations using a single model. However, since the training set is skewed, the network is more confident about up-right faces. * The model does not require additional components such as segmentation, bounding-box regression, segmentation, or SVM classifiers ### How * __Data augmentation__: to increase the number of positive samples (24K face annotations), the authors used randomly sampled sub-windows of the images with IOU > 50% and also randomly flipped these images. In total, there were 20K positive and 20M negative training samples. * __CNN Architecture__: 5 convolutional layers followed by 3 fully-connected. The fully-connected layers were converted to convolutional layers. Non-Maximal Suppression is applied to merge predicted bounding boxes. * __Training__: the CNN was trained using Caffe Library in the AFLW dataset with the following parameters: * Fine-tuning with AlexNet model * Input image size = 227x227 * Batch size = 128 (32+, 96-) * Stride = 32 * __Test__: the model was evaluated on PASCAL FACE, AFW, and FDDB dataset. * __Running time__: since the fully-connected layers were converted to convolutional layers, the input image in running time may be of any size, obtaining a heat map as output. To detect faces of different sizes though, the image is scaled up/down and new heatmaps are obtained. The authors found that rescaling image 3 times per octave gives reasonable good performance.  * The authors realized that the model is more confident about up-right faces than rotated/occluded ones. This trend is because the lack of good training examples to represent such faces in the training process. Better results can be achieved by using better sampling strategies and more sophisticated data augmentation techniques.  * The authors tested different strategies for NMS and the effect of bounding-box regression for improving face detection. They NMS-avg had better performance compared to NMS-max in terms of average precision. On the other hand, adding a bounding-box regressor degraded the performance for both NMS strategies due to the mismatch between annotations of the training set and the test set. This mismatch is mostly for side-view faces. ### Results: * In comparison to R-CNN, the proposed face detector had significantly better performance independent of the NMS strategy. The authors believe the inferior performance of R-CNN due to the loss of recall since selective search may miss some of the face regions; and loss in localization since bounding-box regression is not perfect and may not be able to fully align the segmentation bounding-boxes, provided by selective search, with the ground truth. * In comparison to other state-of-art methods like structural model, TSM and cascade-based methods the DDFD achieve similar or better results. However, this comparison is not completely fair since the most of methods use extra information of pose annotation or information about facial landmarks during the training.  |
On the Effects of Batch and Weight Normalization in Generative Adversarial Networks
Sitao Xiang and Hao Li
arXiv e-Print archive - 2017 via Local arXiv
Keywords: stat.ML, cs.CV, cs.LG
First published: 2017/04/13 (7 years ago)
Abstract: Generative adversarial networks (GANs) are highly effective unsupervised learning frameworks that can generate very sharp data, even for data such as images with complex, highly multimodal distributions. However GANs are known to be very hard to train, suffering from problems such as mode collapse and disturbing visual artifacts. Batch normalization (BN) techniques have been introduced to address the training problem. However, though BN accelerates training in the beginning, our experiments show that the use of BN can be unstable and negatively impact the quality of the trained model. The evaluation of BN and numerous other recent schemes for improving GAN training is hindered by the lack of an effective objective quality measure for GAN models. To address these issues, we first introduce a weight normalization (WN) approach for GAN training that significantly improves the stability, efficiency and the quality of the generated samples. To allow a methodical evaluation, we introduce a new objective measure based on a squared Euclidean reconstruction error metric, to assess training performance in terms of speed, stability, and quality of generated samples. Our experiments indicate that training using WN is generally superior to BN for GANs. We provide statistical evidence for commonly used datasets (CelebA, LSUN, and CIFAR-10), that WN achieves 10% lower mean squared loss for reconstruction and significantly better qualitative results than BN.
more
less
Sitao Xiang and Hao Li
arXiv e-Print archive - 2017 via Local arXiv
Keywords: stat.ML, cs.CV, cs.LG
First published: 2017/04/13 (7 years ago)
Abstract: Generative adversarial networks (GANs) are highly effective unsupervised learning frameworks that can generate very sharp data, even for data such as images with complex, highly multimodal distributions. However GANs are known to be very hard to train, suffering from problems such as mode collapse and disturbing visual artifacts. Batch normalization (BN) techniques have been introduced to address the training problem. However, though BN accelerates training in the beginning, our experiments show that the use of BN can be unstable and negatively impact the quality of the trained model. The evaluation of BN and numerous other recent schemes for improving GAN training is hindered by the lack of an effective objective quality measure for GAN models. To address these issues, we first introduce a weight normalization (WN) approach for GAN training that significantly improves the stability, efficiency and the quality of the generated samples. To allow a methodical evaluation, we introduce a new objective measure based on a squared Euclidean reconstruction error metric, to assess training performance in terms of speed, stability, and quality of generated samples. Our experiments indicate that training using WN is generally superior to BN for GANs. We provide statistical evidence for commonly used datasets (CelebA, LSUN, and CIFAR-10), that WN achieves 10% lower mean squared loss for reconstruction and significantly better qualitative results than BN.
|
[link]
* They analyze the effects of using Batch Normalization (BN) and Weight Normalization (WN) in GANs (classical algorithm, like DCGAN).
* They introduce a new measure to rate the quality of the generated images over time.
### How
* They use BN as it is usually defined.
* They use WN with the following formulas:
* Strict weight-normalized layer:
* 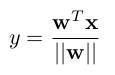
* Affine weight-normalized layer:
* 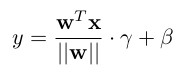
* As activation units they use Translated ReLUs (aka "threshold functions"):
* 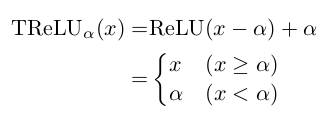
* `alpha` is a learned parameter.
* TReLUs play better with their WN layers than normal ReLUs.
* Reconstruction measure
* To evaluate the quality of the generated images during training, they introduce a new measure.
* The measure is based on a L2-Norm (MSE) between (1) a real image and (2) an image created by the generator that is as similar as possible to the real image.
* They generate (2) by starting `G(z)` with a noise vector `z` that is filled with zeros. The desired output is the real image. They compute a MSE between the generated and real image and backpropagate the result. Then they use the generated gradient to update `z`, while leaving the parameters of `G` unaltered. They repeat this for a defined number of steps.
* Note that the above described method is fairly time-consuming, so they don't do it often.
* Networks
* Their networks are fairly standard.
* Generator: Starts at 1024 filters, goes down to 64 (then 3 for the output). Upsampling via fractionally strided convs.
* Discriminator: Starts at 64 filters, goes to 1024 (then 1 for the output). Downsampling via strided convolutions.
* They test three variations of these networks:
* Vanilla: No normalization. PReLUs in both G and D.
* BN: BN in G and D, but not in the last layers and not in the first layer of D. PReLUs in both G and D.
* WN: Strict weight-normalized layers in G and D, except for the last layers, which are affine weight-normalized layers. TPReLUs (Translated PReLUs) in both G and D.
* Other
* They train with RMSProp and batch size 32.
### Results
* Their WN formulation trains stable, provided the learning rate is set to 0.0002 or lower.
* They argue, that their achieved stability is similar to the one in WGAN.
* BN had significant swings in quality.
* Vanilla collapsed sooner or later.
* Both BN and Vanilla reached an optimal point shortly after the start of the training. After that, the quality of the generated images only worsened.
* Plot of their quality measure:
* 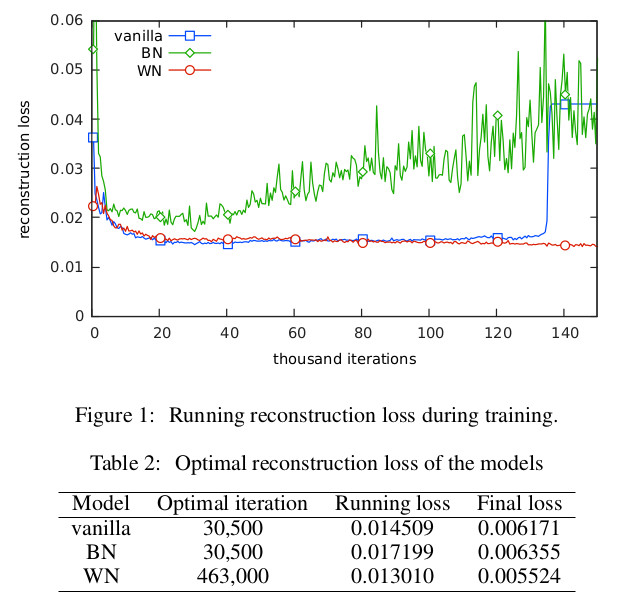
* Their quality measure is based on reconstruction of input images. The below image shows examples for that reconstruction (each person: original image, vanilla reconstruction, BN rec., WN rec.).
* 
* Examples generated by their WN network:
* 
 |
Weight Normalization: A Simple Reparameterization to Accelerate Training of Deep Neural Networks
Salimans, Tim and Kingma, Diederik P.
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
Salimans, Tim and Kingma, Diederik P.
Neural Information Processing Systems Conference - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* Weight Normalization (WN) is a normalization technique, similar to Batch Normalization (BN).
* It normalizes each layer's weights.
### Differences to BN
* WN normalizes based on each weight vector's orientation and magnitude. BN normalizes based on each weight's mean and variance in a batch.
* WN works on each example on its own. BN works on whole batches.
* WN is more deterministic than BN (due to not working an batches).
* WN is better suited for noisy environment (RNNs, LSTMs, reinforcement learning, generative models). (Due to being more deterministic.)
* WN is computationally simpler than BN.
### How its done
* WN is a module added on top of a linear or convolutional layer.
* If that layer's weights are `w` then WN learns two parameters `g` (scalar) and `v` (vector, identical dimension to `w`) so that `w = gv / ||v||` is fullfilled (`||v||` = euclidean norm of v).
* `g` is the magnitude of the weights, `v` are their orientation.
* `v` is initialized to zero mean and a standard deviation of 0.05.
* For networks without recursions (i.e. not RNN/LSTM/GRU):
* Right after initialization, they feed a single batch through the network.
* For each neuron/weight, they calculate the mean and standard deviation after the WN layer.
* They then adjust the bias to `-mean/stdDev` and `g` to `1/stdDev`.
* That makes the network start with each feature being roughly zero-mean and unit-variance.
* The same method can also be applied to networks without WN.
### Results:
* They define BN-MEAN as a variant of BN which only normalizes to zero-mean (not unit-variance).
* CIFAR-10 image classification (no data augmentation, some dropout, some white noise):
* WN, BN, BN-MEAN all learn similarly fast. Network without normalization learns slower, but catches up towards the end.
* BN learns "more" per example, but is about 16% slower (time-wise) than WN.
* WN reaches about same test error as no normalization (both ~8.4%), BN achieves better results (~8.0%).
* WN + BN-MEAN achieves best results with 7.31%.
* Optimizer: Adam
* Convolutional VAE on MNIST and CIFAR-10:
* WN learns more per example und plateaus at better values than network without normalization. (BN was not tested.)
* Optimizer: Adamax
* DRAW on MNIST (heavy on LSTMs):
* WN learns significantly more example than network without normalization.
* Also ends up with better results. (Normal network might catch up though if run longer.)
* Deep Reinforcement Learning (Space Invaders):
* WN seemed to overall acquire a bit more reward per epoch than network without normalization. Variance (in acquired reward) however also grew.
* Results not as clear as in DRAW.
* Optimizer: Adamax
### Extensions
* They argue that initializing `g` to `exp(cs)` (`c` constant, `s` learned) might be better, but they didn't get better test results with that.
* Due to some gradient effects, `||v||` currently grows monotonically with every weight update. (Not necessarily when using optimizers that use separate learning rates per parameters.)
* That grow effect leads the network to be more robust to different learning rates.
* Setting a small hard limit/constraint for `||v||` can lead to better test set performance (parameter updates are larger, introducing more noise).

*Performance of WN on CIFAR-10 compared to BN, BN-MEAN and no normalization.*

*Performance of WN for DRAW (left) and deep reinforcement learning (right).*
 |
Inception-v4, Inception-ResNet and the Impact of Residual Connections on Learning
Szegedy, Christian and Ioffe, Sergey and Vanhoucke, Vincent
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Szegedy, Christian and Ioffe, Sergey and Vanhoucke, Vincent
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* Inception v4 is like Inception v3, but
* Slimmed down, i.e. some parts were simplified
* One new version with residual connections (Inception-ResNet-v2), one without (Inception-v4)
* They didn't observe an improved error rate when using residual connections.
* They did however oberserve that using residual connections decreased their training times.
* They had to scale down the results of their residual modules (multiply them by a constant ~0.1). Otherwise their networks would die (only produce 0s).
* Results on ILSVRC 2012 (val set, 144 crops/image):
* Top-1 Error:
* Inception-v4: 17.7%
* Inception-ResNet-v2: 17.8%
* Top-5 Error (ILSVRC 2012 val set, 144 crops/image):
* Inception-v4: 3.8%
* Inception-ResNet-v2: 3.7%
### Architecture
* Basic structure of Inception-ResNet-v2 (layers, dimensions):
* `Image -> Stem -> 5x Module A -> Reduction-A -> 10x Module B -> Reduction B -> 5x Module C -> AveragePooling -> Droput 20% -> Linear, Softmax`
* `299x299x3 -> 35x35x256 -> 35x35x256 -> 17x17x896 -> 17x17x896 -> 8x8x1792 -> 8x8x1792 -> 1792 -> 1792 -> 1000`
* Modules A, B, C are very similar.
* They contain 2 (B, C) or 3 (A) branches.
* Each branch starts with a 1x1 convolution on the input.
* All branches merge into one 1x1 convolution (which is then added to the original input, as usually in residual architectures).
* Module A uses 3x3 convolutions, B 7x1 and 1x7, C 3x1 and 1x3.
* The reduction modules also contain multiple branches. One has max pooling (3x3 stride 2), the other branches end in convolutions with stride 2.




*From top to bottom: Module A, Module B, Module C, Reduction Module A.*

*Top 5 eror by epoch, models with (red, solid, bottom) and without (green, dashed) residual connections.*
-------------------------
### Rough chapter-wise notes
### Introduction, Related Work
* Inception v3 was adapted to run on DistBelief. Inception v4 is designed for TensorFlow, which gets rid of some constraints and allows a simplified architecture.
* Authors don't think that residual connections are inherently needed to train deep nets, but they do speed up the training.
* History:
* Inception v1 - Introduced inception blocks
* Inception v2 - Added Batch Normalization
* Inception v3 - Factorized the inception blocks further (more submodules)
* Inception v4 - Adds residual connections
### Architectural Choices
* Previous architectures were constrained due to memory problems. TensorFlow got rid of that problem.
* Previous architectures were carefully/conservatively extended. Architectures ended up being quite complicated. This version slims down everything.
* They had problems with residual networks dieing when they contained more than 1000 filters (per inception module apparently?). They could fix that by multiplying the results of the residual subnetwork (before the element-wise addition) with a constant factor of ~0.1.
### Training methodology
* Kepler GPUs, TensorFlow, RMSProb (SGD+Momentum apprently performed worse)
### Experimental Results
* Their residual version of Inception v4 ("Inception-ResNet-v2") seemed to learn faster than the non-residual version.
* They both peaked out at almost the same value.
* Top-1 Error (ILSVRC 2012 val set, 144 crops/image):
* Inception-v4: 17.7%
* Inception-ResNet-v2: 17.8%
* Top-5 Error (ILSVRC 2012 val set, 144 crops/image):
* Inception-v4: 3.8%
* Inception-ResNet-v2: 3.7%
 |
Generative Adversarial Nets
Goodfellow, Ian J. and Pouget-Abadie, Jean and Mirza, Mehdi and Xu, Bing and Warde-Farley, David and Ozair, Sherjil and Courville, Aaron C. and Bengio, Yoshua
Neural Information Processing Systems Conference - 2014 via Local Bibsonomy
Keywords: dblp
Goodfellow, Ian J. and Pouget-Abadie, Jean and Mirza, Mehdi and Xu, Bing and Warde-Farley, David and Ozair, Sherjil and Courville, Aaron C. and Bengio, Yoshua
Neural Information Processing Systems Conference - 2014 via Local Bibsonomy
Keywords: dblp
|
[link]
* GANs are based on adversarial training.
* Adversarial training is a basic technique to train generative models (so here primarily models that create new images).
* In an adversarial training one model (G, Generator) generates things (e.g. images). Another model (D, discriminator) sees real things (e.g. real images) as well as fake things (e.g. images from G) and has to learn how to differentiate the two.
* Neural Networks are models that can be trained in an adversarial way (and are the only models discussed here).
### How
* G is a simple neural net (e.g. just one fully connected hidden layer). It takes a vector as input (e.g. 100 dimensions) and produces an image as output.
* D is a simple neural net (e.g. just one fully connected hidden layer). It takes an image as input and produces a quality rating as output (0-1, so sigmoid).
* You need a training set of things to be generated, e.g. images of human faces.
* Let the batch size be B.
* G is trained the following way:
* Create B vectors of 100 random values each, e.g. sampled uniformly from [-1, +1]. (Number of values per components depends on the chosen input size of G.)
* Feed forward the vectors through G to create new images.
* Feed forward the images through D to create ratings.
* Use a cross entropy loss on these ratings. All of these (fake) images should be viewed as label=0 by D. If D gives them label=1, the error will be low (G did a good job).
* Perform a backward pass of the errors through D (without training D). That generates gradients/errors per image and pixel.
* Perform a backward pass of these errors through G to train G.
* D is trained the following way:
* Create B/2 images using G (again, B/2 random vectors, feed forward through G).
* Chose B/2 images from the training set. Real images get label=1.
* Merge the fake and real images to one batch. Fake images get label=0.
* Feed forward the batch through D.
* Measure the error using cross entropy.
* Perform a backward pass with the error through D.
* Train G for one batch, then D for one (or more) batches. Sometimes D can be too slow to catch up with D, then you need more iterations of D per batch of G.
### Results
* Good looking images MNIST-numbers and human faces. (Grayscale, rather homogeneous datasets.)
* Not so good looking images of CIFAR-10. (Color, rather heterogeneous datasets.)

*Faces generated by MLP GANs. (Rightmost column shows examples from the training set.)*
-------------------------
### Rough chapter-wise notes
* Introduction
* Discriminative models performed well so far, generative models not so much.
* Their suggested new architecture involves a generator and a discriminator.
* The generator learns to create content (e.g. images), the discriminator learns to differentiate between real content and generated content.
* Analogy: Generator produces counterfeit art, discriminator's job is to judge whether a piece of art is a counterfeit.
* This principle could be used with many techniques, but they use neural nets (MLPs) for both the generator as well as the discriminator.
* Adversarial Nets
* They have a Generator G (simple neural net)
* G takes a random vector as input (e.g. vector of 100 random values between -1 and +1).
* G creates an image as output.
* They have a Discriminator D (simple neural net)
* D takes an image as input (can be real or generated by G).
* D creates a rating as output (quality, i.e. a value between 0 and 1, where 0 means "probably fake").
* Outputs from G are fed into D. The result can then be backpropagated through D and then G. G is trained to maximize log(D(image)), so to create a high value of D(image).
* D is trained to produce only 1s for images from G.
* Both are trained simultaneously, i.e. one batch for G, then one batch for D, then one batch for G...
* D can also be trained multiple times in a row. That allows it to catch up with G.
* Theoretical Results
* Let
* pd(x): Probability that image `x` appears in the training set.
* pg(x): Probability that image `x` appears in the images generated by G.
* If G is now fixed then the best possible D classifies according to: `D(x) = pd(x) / (pd(x) + pg(x))`
* It is proofable that there is only one global optimum for GANs, which is reached when G perfectly replicates the training set probability distribution. (Assuming unlimited capacity of the models and unlimited training time.)
* It is proofable that G and D will converge to the global optimum, so long as D gets enough steps per training iteration to model the distribution generated by G. (Again, assuming unlimited capacity/time.)
* Note that these things are proofed for the general principle for GANs. Implementing GANs with neural nets can then introduce problems typical for neural nets (e.g. getting stuck in saddle points).
* Experiments
* They tested on MNIST, Toronto Face Database (TFD) and CIFAR-10.
* They used MLPs for G and D.
* G contained ReLUs and Sigmoids.
* D contained Maxouts.
* D had Dropout, G didn't.
* They use a Parzen Window Estimate aka KDE (sigma obtained via cross validation) to estimate the quality of their images.
* They note that KDE is not really a great technique for such high dimensional spaces, but its the only one known.
* Results on MNIST and TDF are great. (Note: both grayscale)
* CIFAR-10 seems to match more the texture but not really the structure.
* Noise is noticeable in CIFAR-10 (a bit in TFD too). Comes from MLPs (no convolutions).
* Their KDE score for MNIST and TFD is competitive or better than other approaches.
* Advantages and Disadvantages
* Advantages
* No Markov Chains, only backprob
* Inference-free training
* Wide variety of functions can be incorporated into the model (?)
* Generator never sees any real example. It only gets gradients. (Prevents overfitting?)
* Can represent a wide variety of distributions, including sharp ones (Markov chains only work with blurry images).
* Disadvantages
* No explicit representation of the distribution modeled by G (?)
* D and G must be well synchronized during training
* If G is trained to much (i.e. D can't catch up), it can collapse many components of the random input vectors to the same output ("Helvetica")
 |
Fractional Max-Pooling
Benjamin Graham
arXiv e-Print archive - 2014 via Local arXiv
Keywords: cs.CV
First published: 2014/12/18 (9 years ago)
Abstract: Convolutional networks almost always incorporate some form of spatial pooling, and very often it is alpha times alpha max-pooling with alpha=2. Max-pooling act on the hidden layers of the network, reducing their size by an integer multiplicative factor alpha. The amazing by-product of discarding 75% of your data is that you build into the network a degree of invariance with respect to translations and elastic distortions. However, if you simply alternate convolutional layers with max-pooling layers, performance is limited due to the rapid reduction in spatial size, and the disjoint nature of the pooling regions. We have formulated a fractional version of max-pooling where alpha is allowed to take non-integer values. Our version of max-pooling is stochastic as there are lots of different ways of constructing suitable pooling regions. We find that our form of fractional max-pooling reduces overfitting on a variety of datasets: for instance, we improve on the state-of-the art for CIFAR-100 without even using dropout.
more
less
Benjamin Graham
arXiv e-Print archive - 2014 via Local arXiv
Keywords: cs.CV
First published: 2014/12/18 (9 years ago)
Abstract: Convolutional networks almost always incorporate some form of spatial pooling, and very often it is alpha times alpha max-pooling with alpha=2. Max-pooling act on the hidden layers of the network, reducing their size by an integer multiplicative factor alpha. The amazing by-product of discarding 75% of your data is that you build into the network a degree of invariance with respect to translations and elastic distortions. However, if you simply alternate convolutional layers with max-pooling layers, performance is limited due to the rapid reduction in spatial size, and the disjoint nature of the pooling regions. We have formulated a fractional version of max-pooling where alpha is allowed to take non-integer values. Our version of max-pooling is stochastic as there are lots of different ways of constructing suitable pooling regions. We find that our form of fractional max-pooling reduces overfitting on a variety of datasets: for instance, we improve on the state-of-the art for CIFAR-100 without even using dropout.
|
[link]
* Traditionally neural nets use max pooling with 2x2 grids (2MP).
* 2MP reduces the image dimensions by a factor of 2.
* An alternative would be to use pooling schemes that reduce by factors other than two, e.g. `1 < factor < 2`.
* Pooling by a factor of `sqrt(2)` would allow twice as many pooling layers as 2MP, resulting in "softer" image size reduction throughout the network.
* Fractional Max Pooling (FMP) is such a method to perform max pooling by factors other than 2.
### How
* In 2MP you move a 2x2 grid always by 2 pixels.
* Imagine that these step sizes follow a sequence, i.e. for 2MP: `2222222...`
* If you mix in just a single `1` you get a pooling factor of `<2`.
* By chosing the right amount of `1s` vs. `2s` you can pool by any factor between 1 and 2.
* The sequences of `1s` and `2s` can be generated in fully *random* order or in *pseudorandom* order, where pseudorandom basically means "predictable sub patterns" (e.g. 211211211211211...).
* FMP can happen *disjoint* or *overlapping*. Disjoint means 2x2 grids, overlapping means 3x3.
### Results
* FMP seems to perform generally better than 2MP.
* Better results on various tests, including CIFAR-10 and CIFAR-100 (often quite significant improvement).
* Best configuration seems to be *random* sequences with *overlapping* regions.
* Results are especially better if each test is repeated multiple times per image (as the random sequence generation creates randomness, similar to dropout). First 5-10 repetitions seem to be most valuable, but even 100+ give some improvement.
* An FMP-factor of `sqrt(2)` was usually used.

*Random FMP with a factor of sqrt(2) applied five times to the same input image (results upscaled back to original size).*
-------------------------
### Rough chapter-wise notes
* (1) Convolutional neural networks
* Advantages of 2x2 max pooling (2MP): fast; a bit invariant to translations and distortions; quick reduction of image sizes
* Disadvantages: "disjoint nature of pooling regions" can limit generalization (i.e. that they don't overlap?); reduction of image sizes can be too quick
* Alternatives to 2MP: 3x3 pooling with stride 2, stochastic 2x2 pooling
* All suggested alternatives to 2MP also reduce sizes by a factor of 2
* Author wants to have reduction by sqrt(2) as that would enable to use twice as many pooling layers
* Fractional Max Pooling = Pooling that reduces image sizes by a factor of `1 < alpha < 2`
* FMP introduces randomness into pooling (by the choice of pooling regions)
* Settings of FMP:
* Pooling Factor `alpha` in range [1, 2] (1 = no change in image sizes, 2 = image sizes get halfed)
* Choice of Pooling-Regions: Random or pseudorandom. Random is stronger (?). Random+Dropout can result in underfitting.
* Disjoint or overlapping pooling regions. Results for overlapping are better.
* (2) Fractional max-pooling
* For traditional 2MP, every grid's top left coordinate is at `(2i-1, 2j-1)` and it's bottom right coordinate at `(2i, 2j)` (i=col, j=row).
* It will reduce the original size N to 1/2N, i.e. `2N_in = N_out`.
* Paper analyzes `1 < alpha < 2`, but `alpha > 2` is also possible.
* Grid top left positions can be described by sequences of integers, e.g. (only column): 1, 3, 5, ...
* Disjoint 2x2 pooling might be 1, 3, 5, ... while overlapping would have the same sequence with a larger 3x3 grid.
* The increment of the sequences can be random or pseudorandom for alphas < 2.
* For 2x2 FMP you can represent any alpha with a "good" sequence of increments that all have values `1` or `2`, e.g. 2111121122111121...
* In the case of random FMP, the optimal fraction of 1s and 2s is calculated. Then a random permutation of a sequence of 1s and 2s is generated.
* In the case of pseudorandom FMP, the 1s and 2s follow a pattern that leads to the correct alpha, e.g. 112112121121211212...
* Random FMP creates varying distortions of the input image. Pseudorandom FMP is a faithful downscaling.
* (3) Implementation
* In their tests they use a convnet starting with 10 convolutions, then 20, then 30, ...
* They add FMP with an alpha of sqrt(2) after every conv layer.
* They calculate the desired output size, then go backwards through their network to the input. They multiply the size of the image by sqrt(2) with every FMP layer and add a flat 1 for every conv layer. The result is the required image size. They pad the images to that size.
* They use dropout, with increasing strength from 0% to 50% towards the output.
* They use LeakyReLUs.
* Every time they apply an FMP layer, they generate a new sequence of 1s and 2s. That indirectly makes the network an ensemble of similar networks.
* The output of the network can be averaged over several forward passes (for the same image). The result then becomes more accurate (especially up to >=6 forward passes).
* (4) Results
* Tested on MNIST and CIFAR-100
* Architectures (somehow different from (3)?):
* MNIST: 36x36 img -> 6 times (32 conv (3x3?) -> FMP alpha=sqrt(2)) -> ? -> ? -> output
* CIFAR-100: 94x94 img -> 12 times (64 conv (3x3?) -> FMP alpha=2^(1/3)) -> ? -> ? -> output
* Overlapping pooling regions seemed to perform better than disjoint regions.
* Random FMP seemed to perform better than pseudorandom FMP.
* Other tests:
* "The Online Handwritten Assamese Characters Dataset": FMP performed better than 2MP (though their network architecture seemed to have significantly more parameters
* "CASIA-OLHWDB1.1 database": FMP performed better than 2MP (again, seemed to have more parameters)
* CIFAR-10: FMP performed better than current best network (especially with many tests per image)
 |
Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs)
Djork-Arné Clevert and Thomas Unterthiner and Sepp Hochreiter
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.LG
First published: 2015/11/23 (8 years ago)
Abstract: We introduce the "exponential linear unit" (ELU) which speeds up learning in deep neural networks and leads to higher classification accuracies. Like rectified linear units (ReLUs), leaky ReLUs (LReLUs) and parametrized ReLUs (PReLUs), ELUs alleviate the vanishing gradient problem via the identity for positive values. However, ELUs have improved learning characteristics compared to the units with other activation functions. In contrast to ReLUs, ELUs have negative values which allows them to push mean unit activations closer to zero like batch normalization but with lower computational complexity. Mean shifts toward zero speed up learning by bringing the normal gradient closer to the unit natural gradient because of a reduced bias shift effect. While LReLUs and PReLUs have negative values, too, they do not ensure a noise-robust deactivation state. ELUs saturate to a negative value with smaller inputs and thereby decrease the forward propagated variation and information. Therefore, ELUs code the degree of presence of particular phenomena in the input, while they do not quantitatively model the degree of their absence. In experiments, ELUs lead not only to faster learning, but also to significantly better generalization performance than ReLUs and LReLUs on networks with more than 5 layers. On CIFAR-100 ELUs networks significantly outperform ReLU networks with batch normalization while batch normalization does not improve ELU networks. ELU networks are among the top 10 reported CIFAR-10 results and yield the best published result on CIFAR-100, without resorting to multi-view evaluation or model averaging. On ImageNet, ELU networks considerably speed up learning compared to a ReLU network with the same architecture, obtaining less than 10% classification error for a single crop, single model network.
more
less
Djork-Arné Clevert and Thomas Unterthiner and Sepp Hochreiter
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.LG
First published: 2015/11/23 (8 years ago)
Abstract: We introduce the "exponential linear unit" (ELU) which speeds up learning in deep neural networks and leads to higher classification accuracies. Like rectified linear units (ReLUs), leaky ReLUs (LReLUs) and parametrized ReLUs (PReLUs), ELUs alleviate the vanishing gradient problem via the identity for positive values. However, ELUs have improved learning characteristics compared to the units with other activation functions. In contrast to ReLUs, ELUs have negative values which allows them to push mean unit activations closer to zero like batch normalization but with lower computational complexity. Mean shifts toward zero speed up learning by bringing the normal gradient closer to the unit natural gradient because of a reduced bias shift effect. While LReLUs and PReLUs have negative values, too, they do not ensure a noise-robust deactivation state. ELUs saturate to a negative value with smaller inputs and thereby decrease the forward propagated variation and information. Therefore, ELUs code the degree of presence of particular phenomena in the input, while they do not quantitatively model the degree of their absence. In experiments, ELUs lead not only to faster learning, but also to significantly better generalization performance than ReLUs and LReLUs on networks with more than 5 layers. On CIFAR-100 ELUs networks significantly outperform ReLU networks with batch normalization while batch normalization does not improve ELU networks. ELU networks are among the top 10 reported CIFAR-10 results and yield the best published result on CIFAR-100, without resorting to multi-view evaluation or model averaging. On ImageNet, ELU networks considerably speed up learning compared to a ReLU network with the same architecture, obtaining less than 10% classification error for a single crop, single model network.
|
[link]
* ELUs are an activation function
* The are most similar to LeakyReLUs and PReLUs
### How (formula)
* f(x):
* `if x >= 0: x`
* `else: alpha(exp(x)-1)`
* f'(x) / Derivative:
* `if x >= 0: 1`
* `else: f(x) + alpha`
* `alpha` defines at which negative value the ELU saturates.
* E. g. `alpha=1.0` means that the minimum value that the ELU can reach is `-1.0`
* LeakyReLUs however can go to `-Infinity`, ReLUs can't go below 0.
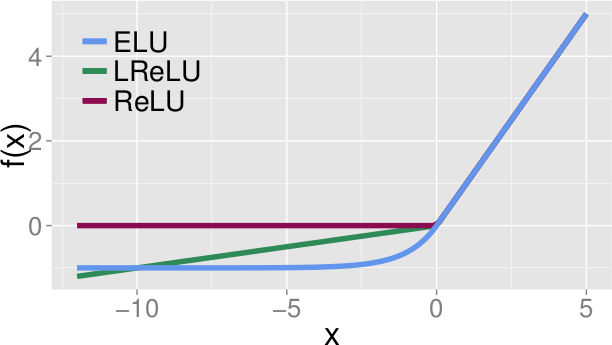
*Form of ELUs(alpha=1.0) vs LeakyReLUs vs ReLUs.*
### Why
* They derive from the unit natural gradient that a network learns faster, if the mean activation of each neuron is close to zero.
* ReLUs can go above 0, but never below. So their mean activation will usually be quite a bit above 0, which should slow down learning.
* ELUs, LeakyReLUs and PReLUs all have negative slopes, so their mean activations should be closer to 0.
* In contrast to LeakyReLUs and PReLUs, ELUs saturate at a negative value (usually -1.0).
* The authors think that is good, because it lets ELUs encode the degree of presence of input concepts, while they do not quantify the degree of absence.
* So ELUs can measure the presence of concepts quantitatively, but the absence only qualitatively.
* They think that this makes ELUs more robust to noise.
### Results
* In their tests on MNIST, CIFAR-10, CIFAR-100 and ImageNet, ELUs perform (nearly always) better than ReLUs and LeakyReLUs.
* However, they don't test PReLUs at all and use an alpha of 0.1 for LeakyReLUs (even though 0.33 is afaik standard) and don't test LeakyReLUs on ImageNet (only ReLUs).
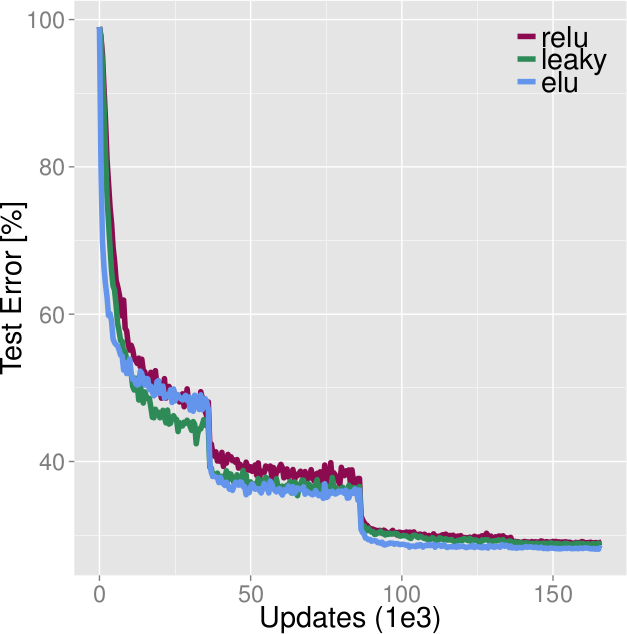
*Comparison of ELUs, LeakyReLUs, ReLUs on CIFAR-100. ELUs ends up with best values, beaten during the early epochs by LeakyReLUs. (Learning rates were optimized for ReLUs.)*
-------------------------
### Rough chapter-wise notes
* Introduction
* Currently popular choice: ReLUs
* ReLU: max(0, x)
* ReLUs are sparse and avoid the vanishing gradient problem, because their derivate is 1 when they are active.
* ReLUs have a mean activation larger than zero.
* Non-zero mean activation causes a bias shift in the next layer, especially if multiple of them are correlated.
* The natural gradient (?) corrects for the bias shift by adjusting the weight update.
* Having less bias shift would bring the standard gradient closer to the natural gradient, which would lead to faster learning.
* Suggested solutions:
* Centering activation functions at zero, which would keep the off-diagonal entries of the Fisher information matrix small.
* Batch Normalization
* Projected Natural Gradient Descent (implicitly whitens the activations)
* These solutions have the problem, that they might end up taking away previous learning steps, which would slow down learning unnecessarily.
* Chosing a good activation function would be a better solution.
* Previously, tanh was prefered over sigmoid for that reason (pushed mean towards zero).
* Recent new activation functions:
* LeakyReLUs: x if x > 0, else alpha*x
* PReLUs: Like LeakyReLUs, but alpha is learned
* RReLUs: Slope of part < 0 is sampled randomly
* Such activation functions with non-zero slopes for negative values seemed to improve results.
* The deactivation state of such units is not very robust to noise, can get very negative.
* They suggest an activation function that can return negative values, but quickly saturates (for negative values, not for positive ones).
* So the model can make a quantitative assessment for positive statements (there is an amount X of A in the image), but only a qualitative negative one (something indicates that B is not in the image).
* They argue that this makes their activation function more robust to noise.
* Their activation function still has activations with a mean close to zero.
* Zero Mean Activations Speed Up Learning
* Natural Gradient = Update direction which corrects the gradient direction with the Fisher Information Matrix
* Hessian-Free Optimization techniques use an extended Gauss-Newton approximation of Hessians and therefore can be interpreted as versions of natural gradient descent.
* Computing the Fisher matrix is too expensive for neural networks.
* Methods to approximate the Fisher matrix or to perform natural gradient descent have been developed.
* Natural gradient = inverse(FisherMatrix) * gradientOfWeights
* Lots of formulas. Apparently first explaining how the natural gradient descent works, then proofing that natural gradient descent can deal well with non-zero-mean activations.
* Natural gradient descent auto-corrects bias shift (i.e. non-zero-mean activations).
* If that auto-correction does not exist, oscillations (?) can occur, which slow down learning.
* Two ways to push means towards zero:
* Unit zero mean normalization (e.g. Batch Normalization)
* Activation functions with negative parts
* Exponential Linear Units (ELUs)
* *Formula*
* f(x):
* if x >= 0: x
* else: alpha(exp(x)-1)
* f'(x) / Derivative:
* if x >= 0: 1
* else: f(x) + alpha
* `alpha` defines at which negative value the ELU saturates.
* `alpha=0.5` => minimum value is -0.5 (?)
* ELUs avoid the vanishing gradient problem, because their positive part is the identity function (like e.g. ReLUs)
* The negative values of ELUs push the mean activation towards zero.
* Mean activations closer to zero resemble more the natural gradient, therefore they should speed up learning.
* ELUs are more noise robust than PReLUs and LeakyReLUs, because their negative values saturate and thus should create a small gradient.
* "ELUs encode the degree of presence of input concepts, while they do not quantify the degree of absence"
* Experiments Using ELUs
* They compare ELUs to ReLUs and LeakyReLUs, but not to PReLUs (no explanation why).
* They seem to use a negative slope of 0.1 for LeakyReLUs, even though 0.33 is standard afaik.
* They use an alpha of 1.0 for their ELUs (i.e. minimum value is -1.0).
* MNIST classification:
* ELUs achieved lower mean activations than ReLU/LeakyReLU
* ELUs achieved lower cross entropy loss than ReLU/LeakyReLU (and also seemed to learn faster)
* They used 5 hidden layers of 256 units each (no explanation why so many)
* (No convolutions)
* MNIST Autoencoder:
* ELUs performed consistently best (at different learning rates)
* Usually ELU > LeakyReLU > ReLU
* LeakyReLUs not far off, so if they had used a 0.33 value maybe these would have won
* CIFAR-100 classification:
* Convolutional network, 11 conv layers
* LeakyReLUs performed better during the first ~50 epochs, ReLUs mostly on par with ELUs
* LeakyReLUs about on par for epochs 50-100
* ELUs win in the end (the learning rates used might not be optimal for ELUs, were designed for ReLUs)
* CIFER-100, CIFAR-10 (big convnet):
* 6.55% error on CIFAR-10, 24.28% on CIFAR-100
* No comparison with ReLUs and LeakyReLUs for same architecture
* ImageNet
* Big convnet with spatial pyramid pooling (?) before the fully connected layers
* Network with ELUs performed better than ReLU network (better score at end, faster learning)
* Networks were still learning at the end, they didn't run till convergence
* No comparison to LeakyReLUs
 |
Deep Residual Learning for Image Recognition
He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian
arXiv e-Print archive - 2015 via Local Bibsonomy
Keywords: dblp
He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian
arXiv e-Print archive - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* Deep plain/ordinary networks usually perform better than shallow networks.
* However, when they get too deep their performance on the *training* set decreases. That should never happen and is a shortcoming of current optimizers.
* If the "good" insights of the early layers could be transferred through the network unaltered, while changing/improving the "bad" insights, that effect might disappear.
### What residual architectures are
* Residual architectures use identity functions to transfer results from previous layers unaltered.
* They change these previous results based on results from convolutional layers.
* So while a plain network might do something like `output = convolution(image)`, a residual network will do `output = image + convolution(image)`.
* If the convolution resorts to just doing nothing, that will make the result a lot worse in the plain network, but not alter it at all in the residual network.
* So in the residual network, the convolution can focus fully on learning what positive changes it has to perform, while in the plain network it *first* has to learn the identity function and then what positive changes it can perform.
### How it works
* Residual architectures can be implemented in most frameworks. You only need something like a split layer and an element-wise addition.
* Use one branch with an identity function and one with 2 or more convolutions (1 is also possible, but seems to perform poorly). Merge them with the element-wise addition.
* Rough example block (for a 64x32x32 input):
https://i.imgur.com/NJVb9hj.png
* An example block when you have to change the dimensionality (e.g. here from 64x32x32 to 128x32x32):
https://i.imgur.com/9NXvTjI.png
* The authors seem to prefer using either two 3x3 convolutions or the chain of 1x1 then 3x3 then 1x1. They use the latter one for their very deep networks.
* The authors also tested:
* To use 1x1 convolutions instead of identity functions everywhere. Performed a bit better than using 1x1 only for dimensionality changes. However, also computation and memory demands.
* To use zero-padding for dimensionality changes (no 1x1 convs, just fill the additional dimensions with zeros). Performed only a bit worse than 1x1 convs and a lot better than plain network architectures.
* Pooling can be used as in plain networks. No special architectures are necessary.
* Batch normalization can be used as usually (before nonlinearities).
### Results
* Residual networks seem to perform generally better than similarly sized plain networks.
* They seem to be able to achieve similar results with less computation.
* They enable well-trainable very deep architectures with up to 1000 layers and more.
* The activations of the residual layers are low compared to plain networks. That indicates that the residual networks indeed only learn to make "good" changes and default to "if in doubt, change nothing".
*Examples of basic building blocks (other architectures are possible). The paper doesn't discuss the placement of the ReLU (after add instead of after the layer).*
*Activations of layers (after batch normalization, before nonlinearity) throughout the network for plain and residual nets. Residual networks have on average lower activations.*
-------------------------
### Rough chapter-wise notes
* (1) Introduction
* In classical architectures, adding more layers can cause the network to perform worse on the training set.
* That shouldn't be the case. (E.g. a shallower could be trained and then get a few layers of identity functions on top of it to create a deep network.)
* To combat that problem, they stack residual layers.
* A residual layer is an identity function and can learn to add something on top of that.
* So if `x` is an input image and `f(x)` is a convolution, they do something like `x + f(x)` or even `x + f(f(x))`.
* The classical architecture would be more like `f(f(f(f(x))))`.
* Residual architectures can be easily implemented in existing frameworks using skip connections with identity functions (split + merge).
* Residual architecture outperformed other in ILSVRC 2015 and COCO 2015.
* (3) Deep Residual Learning
* If some layers have to fit a function `H(x)` then they should also be able to fit `H(x) - x` (change between `x` and `H(x)`).
* The latter case might be easier to learn than the former one.
* The basic structure of a residual block is `y = x + F(x, W)`, where `x` is the input image, `y` is the output image (`x + change`) and `F(x, W)` is the residual subnetwork that estimates a good change of `x` (W are the subnetwork's weights).
* `x` and `F(x, W)` are added using element-wise addition.
* `x` and the output of `F(x, W)` must be have equal dimensions (channels, height, width).
* If different dimensions are required (mainly change in number of channels) a linear projection `V` is applied to `x`: `y = F(x, W) + Vx`. They use a 1x1 convolution for `V` (without nonlinearity?).
* `F(x, W)` subnetworks can contain any number of layer. They suggest 2+ convolutions. Using only 1 layer seems to be useless.
* They run some tests on a network with 34 layers and compare to a 34 layer network without residual blocks and with VGG (19 layers).
* They say that their architecture requires only 18% of the FLOPs of VGG. (Though a lot of that probably comes from VGG's 2x4096 fully connected layers? They don't use any fully connected layers, only convolutions.)
* A critical part is the change in dimensionality (e.g. from 64 kernels to 128). They test (A) adding the new dimensions empty (padding), (B) using the mentioned linear projection with 1x1 convolutions and (C) using the same linear projection, but on all residual blocks (not only for dimensionality changes).
* (A) doesn't add parameters, (B) does (i.e. breaks the pattern of using identity functions).
* They use batch normalization before each nonlinearity.
* Optimizer is SGD.
* They don't use dropout.
* (4) Experiments
* When testing on ImageNet an 18 layer plain (i.e. not residual) network has lower training set error than a deep 34 layer plain network.
* They argue that this effect does probably not come from vanishing gradients, because they (a) checked the gradient norms and they looked healthy and (b) use batch normaliaztion.
* They guess that deep plain networks might have exponentially low convergence rates.
* For the residual architectures its the other way round. Stacking more layers improves the results.
* The residual networks also perform better (in error %) than plain networks with the same number of parameters and layers. (Both for training and validation set.)
* Regarding the previously mentioned handling of dimensionality changes:
* (A) Pad new dimensions: Performs worst. (Still far better than plain network though.)
* (B) Linear projections for dimensionality changes: Performs better than A.
* (C) Linear projections for all residual blocks: Performs better than B. (Authors think that's due to introducing new parameters.)
* They also test on very deep residual networks with 50 to 152 layers.
* For these deep networks their residual block has the form `1x1 conv -> 3x3 conv -> 1x1 conv` (i.e. dimensionality reduction, convolution, dimensionality increase).
* These deeper networks perform significantly better.
* In further tests on CIFAR-10 they can observe that the activations of the convolutions in residual networks are lower than in plain networks.
* So the residual networks default to doing nothing and only change (activate) when something needs to be changed.
* They test a network with 1202 layers. It is still easily optimizable, but overfits the training set.
* They also test on COCO and get significantly better results than a Faster-R-CNN+VGG implementation.
 |
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift
Sergey Ioffe and Christian Szegedy
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.LG
First published: 2015/02/11 (9 years ago)
Abstract: Training Deep Neural Networks is complicated by the fact that the distribution of each layer's inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities. We refer to this phenomenon as internal covariate shift, and address the problem by normalizing layer inputs. Our method draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini-batch. Batch Normalization allows us to use much higher learning rates and be less careful about initialization. It also acts as a regularizer, in some cases eliminating the need for Dropout. Applied to a state-of-the-art image classification model, Batch Normalization achieves the same accuracy with 14 times fewer training steps, and beats the original model by a significant margin. Using an ensemble of batch-normalized networks, we improve upon the best published result on ImageNet classification: reaching 4.9% top-5 validation error (and 4.8% test error), exceeding the accuracy of human raters.
more
less
Sergey Ioffe and Christian Szegedy
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.LG
First published: 2015/02/11 (9 years ago)
Abstract: Training Deep Neural Networks is complicated by the fact that the distribution of each layer's inputs changes during training, as the parameters of the previous layers change. This slows down the training by requiring lower learning rates and careful parameter initialization, and makes it notoriously hard to train models with saturating nonlinearities. We refer to this phenomenon as internal covariate shift, and address the problem by normalizing layer inputs. Our method draws its strength from making normalization a part of the model architecture and performing the normalization for each training mini-batch. Batch Normalization allows us to use much higher learning rates and be less careful about initialization. It also acts as a regularizer, in some cases eliminating the need for Dropout. Applied to a state-of-the-art image classification model, Batch Normalization achieves the same accuracy with 14 times fewer training steps, and beats the original model by a significant margin. Using an ensemble of batch-normalized networks, we improve upon the best published result on ImageNet classification: reaching 4.9% top-5 validation error (and 4.8% test error), exceeding the accuracy of human raters.
|
[link]
### What is BN:
* Batch Normalization (BN) is a normalization method/layer for neural networks.
* Usually inputs to neural networks are normalized to either the range of [0, 1] or [-1, 1] or to mean=0 and variance=1. The latter is called *Whitening*.
* BN essentially performs Whitening to the intermediate layers of the networks.
### How its calculated:
* The basic formula is $x^* = (x - E[x]) / \sqrt{\text{var}(x)}$, where $x^*$ is the new value of a single component, $E[x]$ is its mean within a batch and `var(x)` is its variance within a batch.
* BN extends that formula further to $x^{**} = gamma * x^* +$ beta, where $x^{**}$ is the final normalized value. `gamma` and `beta` are learned per layer. They make sure that BN can learn the identity function, which is needed in a few cases.
* For convolutions, every layer/filter/kernel is normalized on its own (linear layer: each neuron/node/component). That means that every generated value ("pixel") is treated as an example. If we have a batch size of N and the image generated by the convolution has width=P and height=Q, we would calculate the mean (E) over `N*P*Q` examples (same for the variance).
### Theoretical effects:
* BN reduces *Covariate Shift*. That is the change in distribution of activation of a component. By using BN, each neuron's activation becomes (more or less) a gaussian distribution, i.e. its usually not active, sometimes a bit active, rare very active.
* Covariate Shift is undesirable, because the later layers have to keep adapting to the change of the type of distribution (instead of just to new distribution parameters, e.g. new mean and variance values for gaussian distributions).
* BN reduces effects of exploding and vanishing gradients, because every becomes roughly normal distributed. Without BN, low activations of one layer can lead to lower activations in the next layer, and then even lower ones in the next layer and so on.
### Practical effects:
* BN reduces training times. (Because of less Covariate Shift, less exploding/vanishing gradients.)
* BN reduces demand for regularization, e.g. dropout or L2 norm. (Because the means and variances are calculated over batches and therefore every normalized value depends on the current batch. I.e. the network can no longer just memorize values and their correct answers.)
* BN allows higher learning rates. (Because of less danger of exploding/vanishing gradients.)
* BN enables training with saturating nonlinearities in deep networks, e.g. sigmoid. (Because the normalization prevents them from getting stuck in saturating ranges, e.g. very high/low values for sigmoid.)

*BN applied to MNIST (a), and activations of a randomly selected neuron over time (b, c), where the middle line is the median activation, the top line is the 15th percentile and the bottom line is the 85th percentile.*
-------------------------
### Rough chapter-wise notes
* (2) Towards Reducing Covariate Shift
* Batch Normalization (*BN*) is a special normalization method for neural networks.
* In neural networks, the inputs to each layer depend on the outputs of all previous layers.
* The distributions of these outputs can change during the training. Such a change is called a *covariate shift*.
* If the distributions stayed the same, it would simplify the training. Then only the parameters would have to be readjusted continuously (e.g. mean and variance for normal distributions).
* If using sigmoid activations, it can happen that one unit saturates (very high/low values). That is undesired as it leads to vanishing gradients for all units below in the network.
* BN fixes the means and variances of layer inputs to specific values (zero mean, unit variance).
* That accomplishes:
* No more covariate shift.
* Fixes problems with vanishing gradients due to saturation.
* Effects:
* Networks learn faster. (As they don't have to adjust to covariate shift any more.)
* Optimizes gradient flow in the network. (As the gradient becomes less dependent on the scale of the parameters and their initial values.)
* Higher learning rates are possible. (Optimized gradient flow reduces risk of divergence.)
* Saturating nonlinearities can be safely used. (Optimized gradient flow prevents the network from getting stuck in saturated modes.)
* BN reduces the need for dropout. (As it has a regularizing effect.)
* How BN works:
* BN normalizes layer inputs to zero mean and unit variance. That is called *whitening*.
* Naive method: Train on a batch. Update model parameters. Then normalize. Doesn't work: Leads to exploding biases while distribution parameters (mean, variance) don't change.
* A proper method has to include the current example *and* all previous examples in the normalization step.
* This leads to calculating in covariance matrix and its inverse square root. That's expensive. The authors found a faster way.
* (3) Normalization via Mini-Batch Statistics
* Each feature (component) is normalized individually. (Due to cost, differentiability.)
* Normalization according to: `componentNormalizedValue = (componentOldValue - E[component]) / sqrt(Var(component))`
* Normalizing each component can reduce the expressitivity of nonlinearities. Hence the formula is changed so that it can also learn the identiy function.
* Full formula: `newValue = gamma * componentNormalizedValue + beta` (gamma and beta learned per component)
* E and Var are estimated for each mini batch.
* BN is fully differentiable. Formulas for gradients/backpropagation are at the end of chapter 3 (page 4, left).
* (3.1) Training and Inference with Batch-Normalized Networks
* During test time, E and Var of each component can be estimated using all examples or alternatively with moving averages estimated during training.
* During test time, the BN formulas can be simplified to a single linear transformation.
* (3.2) Batch-Normalized Convolutional Networks
* Authors recommend to place BN layers after linear/fully-connected layers and before the ninlinearities.
* They argue that the linear layers have a better distribution that is more likely to be similar to a gaussian.
* Placing BN after the nonlinearity would also not eliminate covariate shift (for some reason).
* Learning a separate bias isn't necessary as BN's formula already contains a bias-like term (beta).
* For convolutions they apply BN equally to all features on a feature map. That creates effective batch sizes of m\*pq, where m is the number of examples in the batch and p q are the feature map dimensions (height, width). BN for linear layers has a batch size of m.
* gamma and beta are then learned per feature map, not per single pixel. (Linear layers: Per neuron.)
* (3.3) Batch Normalization enables higher learning rates
* BN normalizes activations.
* Result: Changes to early layers don't amplify towards the end.
* BN makes it less likely to get stuck in the saturating parts of nonlinearities.
* BN makes training more resilient to parameter scales.
* Usually, large learning rates cannot be used as they tend to scale up parameters. Then any change to a parameter amplifies through the network and can lead to gradient explosions.
* With BN gradients actually go down as parameters increase. Therefore, higher learning rates can be used.
* (something about singular values and the Jacobian)
* (3.4) Batch Normalization regularizes the model
* Usually: Examples are seen on their own by the network.
* With BN: Examples are seen in conjunction with other examples (mean, variance).
* Result: Network can't easily memorize the examples any more.
* Effect: BN has a regularizing effect. Dropout can be removed or decreased in strength.
* (4) Experiments
* (4.1) Activations over time
** They tested BN on MNIST with a 100x100x10 network. (One network with BN before each nonlinearity, another network without BN for comparison.)
** Batch Size was 60.
** The network with BN learned faster. Activations of neurons (their means and variances over several examples) seemed to be more consistent during training.
** Generalization of the BN network seemed to be better.
* (4.2) ImageNet classification
** They applied BN to the Inception network.
** Batch Size was 32.
** During training they used (compared to original Inception training) a higher learning rate with more decay, no dropout, less L2, no local response normalization and less distortion/augmentation.
** They shuffle the data during training (i.e. each batch contains different examples).
** Depending on the learning rate, they either achieve the same accuracy (as in the non-BN network) in 14 times fewer steps (5x learning rate) or a higher accuracy in 5 times fewer steps (30x learning rate).
** BN enables training of Inception networks with sigmoid units (still a bit lower accuracy than ReLU).
** An ensemble of 6 Inception networks with BN achieved better accuracy than the previously best network for ImageNet.
* (5) Conclusion
** BN is similar to a normalization layer suggested by Gülcehre and Bengio. However, they applied it to the outputs of nonlinearities.
** They also didn't have the beta and gamma parameters (i.e. their normalization could not learn the identity function).
 |
A Neural Algorithm of Artistic Style
Leon A. Gatys and Alexander S. Ecker and Matthias Bethge
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.CV, cs.NE, q-bio.NC
First published: 2015/08/26 (8 years ago)
Abstract: In fine art, especially painting, humans have mastered the skill to create unique visual experiences through composing a complex interplay between the content and style of an image. Thus far the algorithmic basis of this process is unknown and there exists no artificial system with similar capabilities. However, in other key areas of visual perception such as object and face recognition near-human performance was recently demonstrated by a class of biologically inspired vision models called Deep Neural Networks. Here we introduce an artificial system based on a Deep Neural Network that creates artistic images of high perceptual quality. The system uses neural representations to separate and recombine content and style of arbitrary images, providing a neural algorithm for the creation of artistic images. Moreover, in light of the striking similarities between performance-optimised artificial neural networks and biological vision, our work offers a path forward to an algorithmic understanding of how humans create and perceive artistic imagery.
more
less
Leon A. Gatys and Alexander S. Ecker and Matthias Bethge
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.CV, cs.NE, q-bio.NC
First published: 2015/08/26 (8 years ago)
Abstract: In fine art, especially painting, humans have mastered the skill to create unique visual experiences through composing a complex interplay between the content and style of an image. Thus far the algorithmic basis of this process is unknown and there exists no artificial system with similar capabilities. However, in other key areas of visual perception such as object and face recognition near-human performance was recently demonstrated by a class of biologically inspired vision models called Deep Neural Networks. Here we introduce an artificial system based on a Deep Neural Network that creates artistic images of high perceptual quality. The system uses neural representations to separate and recombine content and style of arbitrary images, providing a neural algorithm for the creation of artistic images. Moreover, in light of the striking similarities between performance-optimised artificial neural networks and biological vision, our work offers a path forward to an algorithmic understanding of how humans create and perceive artistic imagery.
|
[link]
* The paper describes a method to separate content and style from each other in an image.
* The style can then be transfered to a new image.
* Examples:
* Let a photograph look like a painting of van Gogh.
* Improve a dark beach photo by taking the style from a sunny beach photo.
### How
* They use the pretrained 19-layer VGG net as their base network.
* They assume that two images are provided: One with the *content*, one with the desired *style*.
* They feed the content image through the VGG net and extract the activations of the last convolutional layer. These activations are called the *content representation*.
* They feed the style image through the VGG net and extract the activations of all convolutional layers. They transform each layer to a *Gram Matrix* representation. These Gram Matrices are called the *style representation*.
* How to calculate a *Gram Matrix*:
* Take the activations of a layer. That layer will contain some convolution filters (e.g. 128), each one having its own activations.
* Convert each filter's activations to a (1-dimensional) vector.
* Pick all pairs of filters. Calculate the scalar product of both filter's vectors.
* Add the scalar product result as an entry to a matrix of size `#filters x #filters` (e.g. 128x128).
* Repeat that for every pair to get the Gram Matrix.
* The Gram Matrix roughly represents the *texture* of the image.
* Now you have the content representation (activations of a layer) and the style representation (Gram Matrices).
* Create a new image of the size of the content image. Fill it with random white noise.
* Feed that image through VGG to get its content representation and style representation. (This step will be repeated many times during the image creation.)
* Make changes to the new image using gradient descent to optimize a loss function.
* The loss function has two components:
* The mean squared error between the new image's content representation and the previously extracted content representation.
* The mean squared error between the new image's style representation and the previously extracted style representation.
* Add up both components to get the total loss.
* Give both components a weight to alter for more/less style matching (at the expense of content matching).

*One example input image with different styles added to it.*
-------------------------
### Rough chapter-wise notes
* Page 1
* A painted image can be decomposed in its content and its artistic style.
* Here they use a neural network to separate content and style from each other (and to apply that style to an existing image).
* Page 2
* Representations get more abstract as you go deeper in networks, hence they should more resemble the actual content (as opposed to the artistic style).
* They call the feature responses in higher layers *content representation*.
* To capture style information, they use a method that was originally designed to capture texture information.
* They somehow build a feature space on top of the existing one, that is somehow dependent on correlations of features. That leads to a "stationary" (?) and multi-scale representation of the style.
* Page 3
* They use VGG as their base CNN.
* Page 4
* Based on the extracted style features, they can generate a new image, which has equal activations in these style features.
* The new image should match the style (texture, color, localized structures) of the artistic image.
* The style features become more and more abtstract with higher layers. They call that multi-scale the *style representation*.
* The key contribution of the paper is a method to separate style and content representation from each other.
* These representations can then be used to change the style of an existing image (by changing it so that its content representation stays the same, but its style representation matches the artwork).
* Page 6
* The generated images look most appealing if all features from the style representation are used. (The lower layers tend to reflect small features, the higher layers tend to reflect larger features.)
* Content and style can't be separated perfectly.
* Their loss function has two terms, one for content matching and one for style matching.
* The terms can be increased/decreased to match content or style more.
* Page 8
* Previous techniques work only on limited or simple domains or used non-parametric approaches (see non-photorealistic rendering).
* Previously neural networks have been used to classify the time period of paintings (based on their style).
* They argue that separating content from style might be useful and many other domains (other than transfering style of paintings to images).
* Page 9
* The style representation is gathered by measuring correlations between activations of neurons.
* They argue that this is somehow similar to what "complex cells" in the primary visual system (V1) do.
* They note that deep convnets seem to automatically learn to separate content from style, probably because it is helpful for style-invariant classification.
* Page 9, Methods
* They use the 19 layer VGG net as their basis.
* They use only its convolutional layers, not the linear ones.
* They use average pooling instead of max pooling, as that produced slightly better results.
* Page 10, Methods
* The information about the image that is contained in layers can be visualized. To do that, extract the features of a layer as the labels, then start with a white noise image and change it via gradient descent until the generated features have minimal distance (MSE) to the extracted features.
* The build a style representation by calculating Gram Matrices for each layer.
* Page 11, Methods
* The Gram Matrix is generated in the following way:
* Convert each filter of a convolutional layer to a 1-dimensional vector.
* For a pair of filters i, j calculate the value in the Gram Matrix by calculating the scalar product of the two vectors of the filters.
* Do that for every pair of filters, generating a matrix of size #filters x #filters. That is the Gram Matrix.
* Again, a white noise image can be changed with gradient descent to match the style of a given image (i.e. minimize MSE between two Gram Matrices).
* That can be extended to match the style of several layers by measuring the MSE of the Gram Matrices of each layer and giving each layer a weighting.
* Page 12, Methods
* To transfer the style of a painting to an existing image, proceed as follows:
* Start with a white noise image.
* Optimize that image with gradient descent so that it minimizes both the content loss (relative to the image) and the style loss (relative to the painting).
* Each distance (content, style) can be weighted to have more or less influence on the loss function.
 |
Unsupervised Representation Learning with Deep Convolutional Generative Adversarial Networks
Alec Radford and Luke Metz and Soumith Chintala
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.LG, cs.CV
First published: 2015/11/19 (8 years ago)
Abstract: In recent years, supervised learning with convolutional networks (CNNs) has seen huge adoption in computer vision applications. Comparatively, unsupervised learning with CNNs has received less attention. In this work we hope to help bridge the gap between the success of CNNs for supervised learning and unsupervised learning. We introduce a class of CNNs called deep convolutional generative adversarial networks (DCGANs), that have certain architectural constraints, and demonstrate that they are a strong candidate for unsupervised learning. Training on various image datasets, we show convincing evidence that our deep convolutional adversarial pair learns a hierarchy of representations from object parts to scenes in both the generator and discriminator. Additionally, we use the learned features for novel tasks - demonstrating their applicability as general image representations.
more
less
Alec Radford and Luke Metz and Soumith Chintala
arXiv e-Print archive - 2015 via Local arXiv
Keywords: cs.LG, cs.CV
First published: 2015/11/19 (8 years ago)
Abstract: In recent years, supervised learning with convolutional networks (CNNs) has seen huge adoption in computer vision applications. Comparatively, unsupervised learning with CNNs has received less attention. In this work we hope to help bridge the gap between the success of CNNs for supervised learning and unsupervised learning. We introduce a class of CNNs called deep convolutional generative adversarial networks (DCGANs), that have certain architectural constraints, and demonstrate that they are a strong candidate for unsupervised learning. Training on various image datasets, we show convincing evidence that our deep convolutional adversarial pair learns a hierarchy of representations from object parts to scenes in both the generator and discriminator. Additionally, we use the learned features for novel tasks - demonstrating their applicability as general image representations.
|
[link]
* DCGANs are just a different architecture of GANs.
* In GANs a Generator network (G) generates images. A discriminator network (D) learns to differentiate between real images from the training set and images generated by G.
* DCGANs basically convert the laplacian pyramid technique (many pairs of G and D to progressively upscale an image) to a single pair of G and D.
### How
* Their D: Convolutional networks. No linear layers. No pooling, instead strided layers. LeakyReLUs.
* Their G: Starts with 100d noise vector. Generates with linear layers 1024x4x4 values. Then uses fractionally strided convolutions (move by 0.5 per step) to upscale to 512x8x8. This is continued till Cx32x32 or Cx64x64. The last layer is a convolution to 3x32x32/3x64x64 (Tanh activation).
* The fractionally strided convolutions do basically the same as the progressive upscaling in the laplacian pyramid. So it's basically one laplacian pyramid in a single network and all upscalers are trained jointly leading to higher quality images.
* They use Adam as their optimizer. To decrease instability issues they decreased the learning rate to 0.0002 (from 0.001) and the momentum/beta1 to 0.5 (from 0.9).
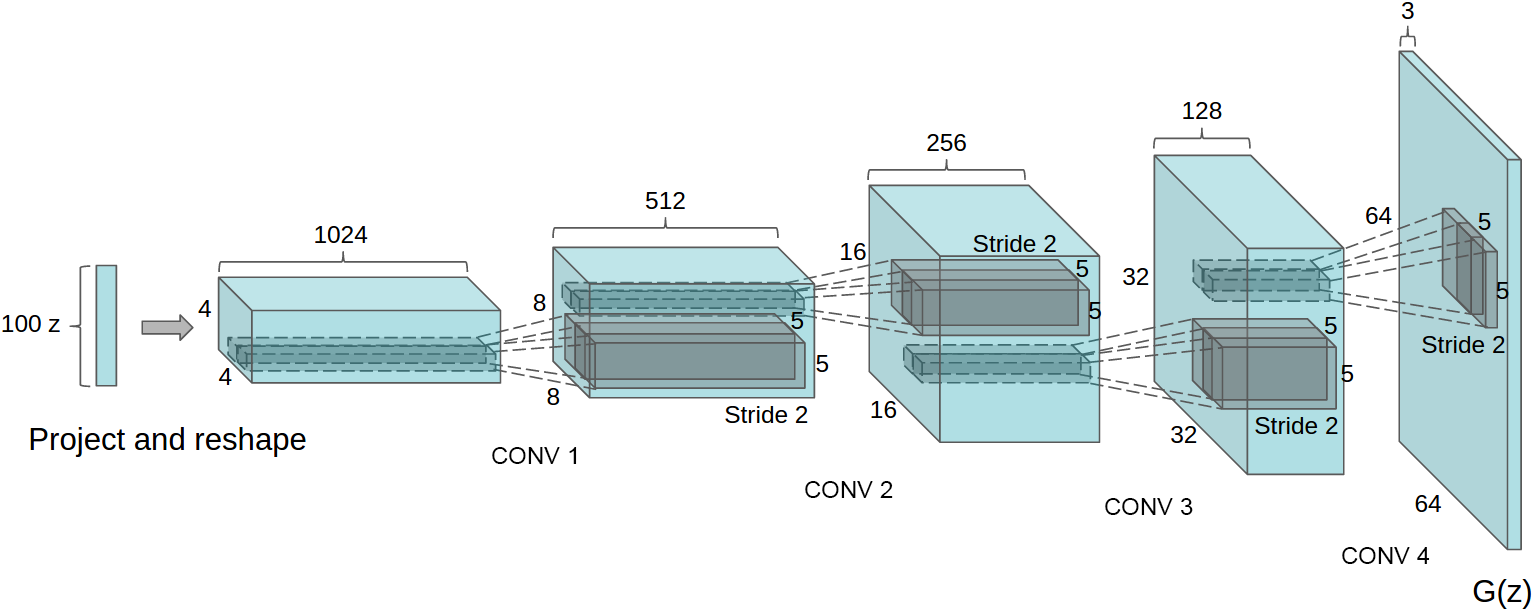
*Architecture of G using fractionally strided convolutions to progressively upscale the image.*
### Results
* High quality images. Still with distortions and errors, but at first glance they look realistic.
* Smooth interpolations between generated images are possible (by interpolating between the noise vectors and feeding these interpolations into G).
* The features extracted by D seem to have some potential for unsupervised learning.
* There seems to be some potential for vector arithmetics (using the initial noise vectors) similar to the vector arithmetics with wordvectors. E.g. to generate mean with sunglasses via `vector(men) + vector(sunglasses)`.
")
*Generated images, bedrooms.*
")
*Generated images, faces.*
### Rough chapter-wise notes
* Introduction
* For unsupervised learning, they propose to use to train a GAN and then reuse the weights of D.
* GANs have traditionally been hard to train.
* Approach and model architecture
* They use for D an convnet without linear layers, withput pooling layers (only strides), LeakyReLUs and Batch Normalization.
* They use for G ReLUs (hidden layers) and Tanh (output).
* Details of adversarial training
* They trained on LSUN, Imagenet-1k and a custom dataset of faces.
* Minibatch size was 128.
* LeakyReLU alpha 0.2.
* They used Adam with a learning rate of 0.0002 and momentum of 0.5.
* They note that a higher momentum lead to oscillations.
* LSUN
* 3M images of bedrooms.
* They use an autoencoder based technique to filter out 0.25M near duplicate images.
* Faces
* They downloaded 3M images of 10k people.
* They extracted 350k faces with OpenCV.
* Empirical validation of DCGANs capabilities
* Classifying CIFAR-10 GANs as a feature extractor
* They train a pair of G and D on Imagenet-1k.
* D's top layer has `512*4*4` features.
* They train an SVM on these features to classify the images of CIFAR-10.
* They achieve a score of 82.8%, better than unsupervised K-Means based methods, but worse than Exemplar CNNs.
* Classifying SVHN digits using GANs as a feature extractor
* They reuse the same pipeline (D trained on CIFAR-10, SVM) for the StreetView House Numbers dataset.
* They use 1000 SVHN images (with the features from D) to train the SVM.
* They achieve 22.48% test error.
* Investigating and visualizing the internals of the networks
* Walking in the latent space
* The performs walks in the latent space (= interpolate between input noise vectors and generate several images for the interpolation).
* They argue that this might be a good way to detect overfitting/memorizations as those might lead to very sudden (not smooth) transitions.
* Visualizing the discriminator features
* They use guided backpropagation to visualize what the feature maps in D have learned (i.e. to which images they react).
* They can show that their LSUN-bedroom GAN seems to have learned in an unsupervised way what beds and windows look like.
* Forgetting to draw certain objects
* They manually annotated the locations of objects in some generated bedroom images.
* Based on these annotations they estimated which feature maps were mostly responsible for generating the objects.
* They deactivated these feature maps and regenerated the images.
* That decreased the appearance of these objects. It's however not as easy as one feature map deactivation leading to one object disappearing. They deactivated quite a lot of feature maps (200) and they objects were often still quite visible or replaced by artefacts/errors.
* Vector arithmetic on face samples
* Wordvectors can be used to perform semantic arithmetic (e.g. `king - man + woman = queen`).
* The unsupervised representations seem to be useable in a similar fashion.
* E.g. they generated images via G. They then picked several images that showed men with glasses and averaged these image's noise vectors. They did with same with men without glasses and women without glasses. Then they performed on these vectors `men with glasses - mean without glasses + women without glasses` to get `woman with glasses
 |
Pixel Recurrent Neural Networks
Oord, Aäron Van Den and Kalchbrenner, Nal and Kavukcuoglu, Koray
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Oord, Aäron Van Den and Kalchbrenner, Nal and Kavukcuoglu, Koray
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
*Note*: This paper felt rather hard to read. The summary might not have hit exactly what the authors tried to explain.
* The authors describe multiple architectures that can model the distributions of images.
* These networks can be used to generate new images or to complete existing ones.
* The networks are mostly based on RNNs.
### How
* They define three architectures:
* Row LSTM:
* Predicts a pixel value based on all previous pixels in the image.
* It applies 1D convolutions (with kernel size 3) to the current and previous rows of the image.
* It uses the convolution results as features to predict a pixel value.
* Diagonal BiLSTM:
* Predicts a pixel value based on all previous pixels in the image.
* Instead of applying convolutions in a row-wise fashion, they apply them to the diagonals towards the top left and top right of the pixel.
* Diagonal convolutions can be applied by padding the n-th row with `n-1` pixels from the left (diagonal towards top left) or from the right (diagonal towards the top right), then apply a 3x1 column convolution.
* PixelCNN:
* Applies convolutions to the region around a pixel to predict its values.
* Uses masks to zero out pixels that follow after the target pixel.
* They use no pooling layers.
* While for the LSTMs each pixel is conditioned on all previous pixels, the dependency range of the CNN is bounded.
* They use up to 12 LSTM layers.
* They use residual connections between their LSTM layers.
* All architectures predict pixel values as a softmax over 255 distinct values (per channel). According to the authors that leads to better results than just using one continuous output (i.e. sigmoid) per channel.
* They also try a multi-scale approach: First, one network generates a small image. Then a second networks generates the full scale image while being conditioned on the small image.
### Results
* The softmax layers learn reasonable distributions. E.g. neighboring colors end up with similar probabilities. Values 0 and 255 tend to have higher probabilities than others, especially for the very first pixel.
* In the 12-layer LSTM row model, residual and skip connections seem to have roughly the same effect on the network's results. Using both yields a tiny improvement over just using one of the techniques alone.
* They achieve a slightly better result on MNIST than DRAW did.
* Their negative log likelihood results for CIFAR-10 improve upon previous models. The diagonal BiLSTM model performs best, followed by the row LSTM model, followed by PixelCNN.
* Their generated images for CIFAR-10 and Imagenet capture real local spatial dependencies. The multi-scale model produces better looking results. The images do not appear blurry. Overall they still look very unreal.

*Generated ImageNet 64x64 images.*

*Completing partially occluded images.*
 |
Generative Moment Matching Networks
Li, Yujia and Swersky, Kevin and Zemel, Richard S.
International Conference on Machine Learning - 2015 via Local Bibsonomy
Keywords: dblp
Li, Yujia and Swersky, Kevin and Zemel, Richard S.
International Conference on Machine Learning - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* Generative Moment Matching Networks (GMMN) are generative models that use maximum mean discrepancy (MMD) for their objective function.
* MMD is a measure of how similar two datasets are (here: generated dataset and training set).
* GMMNs are similar to GANs, but they replace the Discriminator with the MMD measure, making their optimization more stable.
### How
* MMD calculates a similarity measure by comparing statistics of two datasets with each other.
* MMD is calculated based on samples from the training set and the generated dataset.
* A kernel function is applied to pairs of these samples (thus the statistics are acutally calculated in high-dimensional spaces). The authors use Gaussian kernels.
* MMD can be approximated using a small number of samples.
* MMD is differentiable and therefor can be used as a standard loss function.
* They train two models:
* GMMN: Noise vector input (as in GANs), several ReLU layers into one sigmoid layer. MMD as the loss function.
* GMMN+AE: Same as GMMN, but the sigmoid output is not an image, but instead the code that gets fed into an autoencoder's (AE) decoder. The AE is trained separately on the dataset. MMD is backpropagated through the decoder and then the GMMN. I.e. the GMMN learns to produce codes that let the decoder generate good looking images.

*MMD formula, where $x_i$ is a training set example and $y_i$ a generated example.*

*Architectures of GMMN (left) and GMMN+AE (right).*
### Results
* They tested only on MNIST and TFD (i.e. datasets that are well suited for AEs...).
* Their GMMN achieves similar log likelihoods compared to other models.
* Their GMMN+AE achieves better log likelihoods than other models.
* GMMN+AE produces good looking images.
* GMMN+AE produces smooth interpolations between images.

*Generated TFD images and interpolations between them.*
--------------------
### Rough chapter-wise notes
* (1) Introduction
* Sampling in GMMNs is fast.
* GMMNs are similar to GANs.
* While the training objective in GANs is a minimax problem, in GMMNs it is a simple loss function.
* GMMNs are based on maximum mean discrepancy. They use that (implemented via the kernel trick) as the loss function.
* GMMNs try to generate data so that the moments in the generated data are as similar as possible to the moments in the training data.
* They combine GMMNs with autoencoders. That is, they first train an autoencoder to generate images. Then they train a GMMN to produce sound code inputs to the decoder of the autoencoder.
* (2) Maximum Mean Discrepancy
* Maximum mean discrepancy (MMD) is a frequentist estimator to tell whether two datasets X and Y come from the same probability distribution.
* MMD estimates basic statistics values (i.e. mean and higher order statistics) of both datasets and compares them with each other.
* MMD can be formulated so that examples from the datasets are only used for scalar products. Then the kernel trick can be applied.
* It can be shown that minimizing MMD with gaussian kernels is equivalent to matching all moments between the probability distributions of the datasets.
* (4) Generative Moment Matching Networks
* Data Space Networks
* Just like GANs, GMMNs start with a noise vector that has N values sampled uniformly from [-1, 1].
* The noise vector is then fed forward through several fully connected ReLU layers.
* The MMD is differentiable and therefor can be used for backpropagation.
* Auto-Encoder Code Sparse Networks
* AEs can be used to reconstruct high-dimensional data, which is a simpler task than to learn to generate new data from scratch.
* Advantages of using the AE code space:
* Dimensionality can be explicitly chosen.
* Disentangling factors of variation.
* They suggest a combination of GMMN and AE. They first train an AE, then they train a GMMN to generate good codes for the AE's decoder (based on MMD loss).
* For some reason they use greedy layer-wise pretraining with later fine-tuning for the AE, but don't explain why. (That training method is outdated?)
* They add dropout to their AE's encoder to get a smoother code manifold.
* Practical Considerations
* MMD has a bandwidth parameter (as its based on RBFs). Instead of chosing a single fixed bandwidth, they instead use multiple kernels with different bandwidths (1, 5, 10, ...), apply them all and then sum the results.
* Instead of $MMD^2$ loss they use $\sqrt{MMD^2}$, which does not go as fast to zero as raw MMD, thereby creating stronger gradients.
* Per minibatch they generate a small number of samples und they pick a small number of samples from the training set. They then compute MMD for these samples. I.e. they don't run MMD over the whole training set as that would be computationally prohibitive.
* (5) Experiments
* They trained on MNIST and TFD.
* They used an GMMN with 4 ReLU layers and autoencoders with either 2/2 (encoder, decoder) hidden sigmoid layers (MNIST) or 3/3 (TFD).
* They used dropout on the encoder layers.
* They used layer-wise pretraining and finetuning for the AEs.
* They tuned most of the hyperparameters using bayesian optimization.
* They use minibatch sizes of 1000 and compute MMD based on those (i.e. based on 2000 points total).
* Their GMMN+AE model achieves better log likelihood values than all competitors. The raw GMMN model performs roughly on par with the competitors.
* Nearest neighbor evaluation indicates that it did not just memorize the training set.
* The model learns smooth interpolations between digits (MNIST) and faces (TFD).
 |
Generating Images with Perceptual Similarity Metrics based on Deep Networks
Alexey Dosovitskiy and Thomas Brox
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.CV, cs.NE
First published: 2016/02/08 (8 years ago)
Abstract: Image-generating machine learning models are typically trained with loss functions based on distance in the image space. This often leads to over-smoothed results. We propose a class of loss functions, which we call deep perceptual similarity metrics (DeePSiM), that mitigate this problem. Instead of computing distances in the image space, we compute distances between image features extracted by deep neural networks. This metric better reflects perceptually similarity of images and thus leads to better results. We show three applications: autoencoder training, a modification of a variational autoencoder, and inversion of deep convolutional networks. In all cases, the generated images look sharp and resemble natural images.
more
less
Alexey Dosovitskiy and Thomas Brox
arXiv e-Print archive - 2016 via Local arXiv
Keywords: cs.LG, cs.CV, cs.NE
First published: 2016/02/08 (8 years ago)
Abstract: Image-generating machine learning models are typically trained with loss functions based on distance in the image space. This often leads to over-smoothed results. We propose a class of loss functions, which we call deep perceptual similarity metrics (DeePSiM), that mitigate this problem. Instead of computing distances in the image space, we compute distances between image features extracted by deep neural networks. This metric better reflects perceptually similarity of images and thus leads to better results. We show three applications: autoencoder training, a modification of a variational autoencoder, and inversion of deep convolutional networks. In all cases, the generated images look sharp and resemble natural images.
|
[link]
* The authors define in this paper a special loss function (DeePSiM), mostly for autoencoders.
* Usually one would use a MSE of euclidean distance as the loss function for an autoencoder. But that loss function basically always leads to blurry reconstructed images.
* They add two new ingredients to the loss function, which results in significantly sharper looking images.
### How
* Their loss function has three components:
* Euclidean distance in image space (i.e. pixel distance between reconstructed image and original image, as usually used in autoencoders)
* Euclidean distance in feature space. Another pretrained neural net (e.g. VGG, AlexNet, ...) is used to extract features from the original and the reconstructed image. Then the euclidean distance between both vectors is measured.
* Adversarial loss, as usually used in GANs (generative adversarial networks). The autoencoder is here treated as the GAN-Generator. Then a second network, the GAN-Discriminator is introduced. They are trained in the typical GAN-fashion. The loss component for DeePSiM is the loss of the Discriminator. I.e. when reconstructing an image, the autoencoder would learn to reconstruct it in a way that lets the Discriminator believe that the image is real.
* Using the loss in feature space alone would not be enough as that tends to lead to overpronounced high frequency components in the image (i.e. too strong edges, corners, other artefacts).
* To decrease these high frequency components, a "natural image prior" is usually used. Other papers define some function by hand. This paper uses the adversarial loss for that (i.e. learns a good prior).
* Instead of training a full autoencoder (encoder + decoder) it is also possible to only train a decoder and feed features - e.g. extracted via AlexNet - into the decoder.
### Results
* Using the DeePSiM loss with a normal autoencoder results in sharp reconstructed images.
* Using the DeePSiM loss with a VAE to generate ILSVRC-2012 images results in sharp images, which are locally sound, but globally don't make sense. Simple euclidean distance loss results in blurry images.
* Using the DeePSiM loss when feeding only image space features (extracted via AlexNet) into the decoder leads to high quality reconstructions. Features from early layers will lead to more exact reconstructions.
* One can again feed extracted features into the network, but then take the reconstructed image, extract features of that image and feed them back into the network. When using DeePSiM, even after several iterations of that process the images still remain semantically similar, while their exact appearance changes (e.g. a dog's fur color might change, counts of visible objects change).

*Images generated with a VAE using DeePSiM loss.*

*Images reconstructed from features fed into the network. Different AlexNet layers (conv5 - fc8) were used to generate the features. Earlier layers allow more exact reconstruction.*

*First, images are reconstructed from features (AlexNet, layers conv5 - fc8 as columns). Then, features of the reconstructed images are fed back into the network. That is repeated up to 8 times (rows). Images stay semantically similar, but their appearance changes.*
--------------------
### Rough chapter-wise notes
* (1) Introduction
* Using a MSE of euclidean distances for image generation (e.g. autoencoders) often results in blurry images.
* They suggest a better loss function that cares about the existence of features, but not as much about their exact translation, rotation or other local statistics.
* Their loss function is based on distances in suitable feature spaces.
* They use ConvNets to generate those feature spaces, as these networks are sensitive towards important changes (e.g. edges) and insensitive towards unimportant changes (e.g. translation).
* However, naively using the ConvNet features does not yield good results, because the networks tend to project very different images onto the same feature vectors (i.e. they are contractive). That leads to artefacts in the generated images.
* Instead, they combine the feature based loss with GANs (adversarial loss). The adversarial loss decreases the negative effects of the feature loss ("natural image prior").
* (3) Model
* A typical choice for the loss function in image generation tasks (e.g. when using an autoencoders) would be squared euclidean/L2 loss or L1 loss.
* They suggest a new class of losses called "DeePSiM".
* We have a Generator `G`, a Discriminator `D`, a feature space creator `C` (takes an image, outputs a feature space for that image), one (or more) input images `x` and one (or more) target images `y`. Input and target image can be identical.
* The total DeePSiM loss is a weighted sum of three components:
* Feature loss: Squared euclidean distance between the feature spaces of (1) input after fed through G and (2) the target image, i.e. `||C(G(x))-C(y)||^2_2`.
* Adversarial loss: A discriminator is introduced to estimate the "fakeness" of images generated by the generator. The losses for D and G are the standard GAN losses.
* Pixel space loss: Classic squared euclidean distance (as commonly used in autoencoders). They found that this loss stabilized their adversarial training.
* The feature loss alone would create high frequency artefacts in the generated image, which is why a second loss ("natural image prior") is needed. The adversarial loss fulfills that role.
* Architectures
* Generator (G):
* They define different ones based on the task.
* They all use up-convolutions, which they implement by stacking two layers: (1) a linear upsampling layer, then (2) a normal convolutional layer.
* They use leaky ReLUs (alpha=0.3).
* Comparators (C):
* They use variations of AlexNet and Exemplar-CNN.
* They extract the features from different layers, depending on the experiment.
* Discriminator (D):
* 5 convolutions (with some striding; 7x7 then 5x5, afterwards 3x3), into average pooling, then dropout, then 2x linear, then 2-way softmax.
* Training details
* They use Adam with learning rate 0.0002 and normal momentums (0.9 and 0.999).
* They temporarily stop the discriminator training when it gets too good.
* Batch size was 64.
* 500k to 1000k batches per training.
* (4) Experiments
* Autoencoder
* Simple autoencoder with an 8x8x8 code layer between encoder and decoder (so actually more values than in the input image?!).
* Encoder has a few convolutions, decoder a few up-convolutions (linear upsampling + convolution).
* They train on STL-10 (96x96) and take random 64x64 crops.
* Using for C AlexNet tends to break small structural details, using Exempler-CNN breaks color details.
* The autoencoder with their loss tends to produce less blurry images than the common L2 and L1 based losses.
* Training an SVM on the 8x8x8 hidden layer performs significantly with their loss than L2/L1. That indicates potential for unsupervised learning.
* Variational Autoencoder
* They replace part of the standard VAE loss with their DeePSiM loss (keeping the KL divergence term).
* Everything else is just like in a standard VAE.
* Samples generated by a VAE with normal loss function look very blurry. Samples generated with their loss function look crisp and have locally sound statistics, but still (globally) don't really make any sense.
* Inverting AlexNet
* Assume the following variables:
* I: An image
* ConvNet: A convolutional network
* F: The features extracted by a ConvNet, i.e. ConvNet(I) (feaures in all layers, not just the last one)
* Then you can invert the representation of a network in two ways:
* (1) An inversion that takes an F and returns roughly the I that resulted in F (it's *not* key here that ConvNet(reconstructed I) returns the same F again).
* (2) An inversion that takes an F and projects it to *some* I so that ConvNet(I) returns roughly the same F again.
* Similar to the autoencoder cases, they define a decoder, but not encoder.
* They feed into the decoder a feature representation of an image. The features are extracted using AlexNet (they try the features from different layers).
* The decoder has to reconstruct the original image (i.e. inversion scenario 1). They use their DeePSiM loss during the training.
* The images can be reonstructed quite well from the last convolutional layer in AlexNet. Chosing the later fully connected layers results in more errors (specifially in the case of the very last layer).
* They also try their luck with the inversion scenario (2), but didn't succeed (as their loss function does not care about diversity).
* They iteratively encode and decode the same image multiple times (probably means: image -> features via AlexNet -> decode -> reconstructed image -> features via AlexNet -> decode -> ...). They observe, that the image does not get "destroyed", but rather changes semantically, e.g. three apples might turn to one after several steps.
* They interpolate between images. The interpolations are smooth.
 |
DRAW: A Recurrent Neural Network For Image Generation
Gregor, Karol and Danihelka, Ivo and Graves, Alex and Rezende, Danilo Jimenez and Wierstra, Daan
International Conference on Machine Learning - 2015 via Local Bibsonomy
Keywords: dblp
Gregor, Karol and Danihelka, Ivo and Graves, Alex and Rezende, Danilo Jimenez and Wierstra, Daan
International Conference on Machine Learning - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* DRAW = deep recurrent attentive writer
* DRAW is a recurrent autoencoder for (primarily) images that uses attention mechanisms.
* Like all autoencoders it has an encoder, a latent layer `Z` in the "middle" and a decoder.
* Due to the recurrence, there are actually multiple autoencoders, one for each timestep (the number of timesteps is fixed).
* DRAW has attention mechanisms which allow the model to decide where to look at in the input image ("glimpses") and where to write/draw to in the output image.
* If the attention mechanisms are skipped, the model becomes a simple recurrent autoencoder.
* By training the full autoencoder on a dataset and then only using the decoder, one can generate new images that look similar to the dataset images.
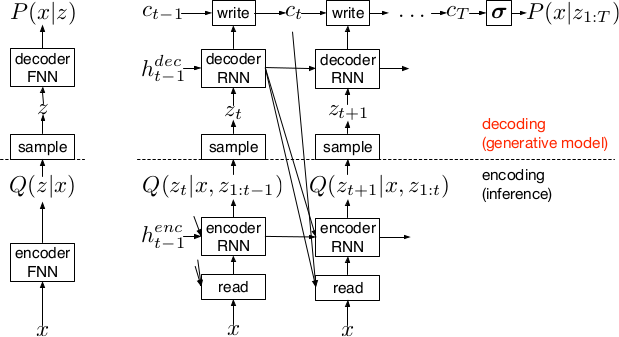
*Basic recurrent architecture of DRAW.*
### How
* General architecture
* The encoder-decoder-pair follows the design of variational autoencoders.
* The latent layer follows an n-dimensional gaussian distribution. The hyperparameters of that distribution (means, standard deviations) are derived from the output of the encoder using a linear transformation.
* Using a gaussian distribution enables the use of the reparameterization trick, which can be useful for backpropagation.
* The decoder receives a sample drawn from that gaussian distribution.
* While the encoder reads from the input image, the decoder writes to an image canvas (where "write" is an addition, not a replacement of the old values).
* The model works in a fixed number of timesteps. At each timestep the encoder performs a read operation and the decoder a write operation.
* Both the encoder and the decoder receive the previous output of the encoder.
* Loss functions
* The loss function of the latent layer is the KL-divergence between that layer's gaussian distribution and a prior, summed over the timesteps.
* The loss function of the decoder is the negative log likelihood of the image given the final canvas content under a bernoulli distribution.
* The total loss, which is optimized, is the expectation of the sum of both losses (latent layer loss, decoder loss).
* Attention
* The selective read attention works on image patches of varying sizes. The result size is always NxN.
* The mechanism has the following parameters:
* `gx`: x-axis coordinate of the center of the patch
* `gy`: y-axis coordinate of the center of the patch
* `delta`: Strides. The higher the strides value, the larger the read image patch.
* `sigma`: Standard deviation. The higher the sigma value, the more blurry the extracted patch will be.
* `gamma`: Intensity-Multiplier. Will be used on the result.
* All of these parameters are generated using a linear transformation applied to the decoder's output.
* The mechanism places a grid of NxN gaussians on the image. The grid is centered at `(gx, gy)`. The gaussians are `delta` pixels apart from each other and have a standard deviation of `sigma`.
* Each gaussian is applied to the image, the center pixel is read and added to the result.
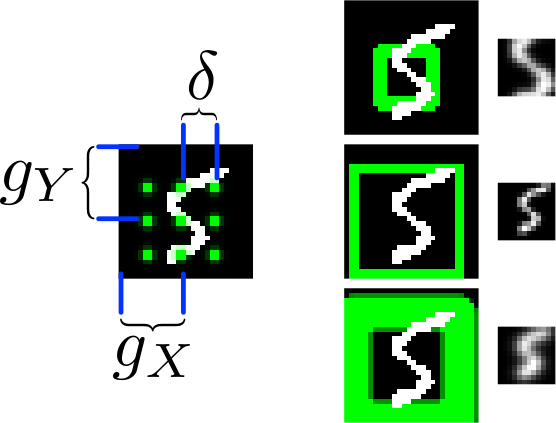
*The basic attention mechanism. (gx, gy) is the read patch center. delta is the strides. On the right: Patches with different sizes/strides and standard deviations/blurriness.*
### Results
* Realistic looking generated images for MNIST and SVHN.
* Structurally OK, but overall blurry images for CIFAR-10.
* Results with attention are usually significantly better than without attention.
* Image generation without attention starts with a blurry image and progressively sharpens it.

*Using DRAW with attention to generate new SVHN images.*
----------
### Rough chapter-wise notes
* 1. Introduction
* The natural way to draw an image is in a step by step way (add some lines, then add some more, etc.).
* Most generative neural networks however create the image in one step.
* That removes the possibility of iterative self-correction, is hard to scale to large images and makes the image generation process dependent on a single latent distribution (input parameters).
* The DRAW architecture generates images in multiple steps, allowing refinements/corrections.
* DRAW is based on varational autoencoders: An encoder compresses images to codes and a decoder generates images from codes.
* The loss function is a variational upper bound on the log-likelihood of the data.
* DRAW uses recurrance to generate images step by step.
* The recurrance is combined with attention via partial glimpses/foveations (i.e. the model sees only a small part of the image).
* Attention is implemented in a differentiable way in DRAW.
* 2. The DRAW Network
* The DRAW architecture is based on variational autoencoders:
* Encoder: Compresses an image to latent codes, which represent the information contained in the image.
* Decoder: Transforms the codes from the encoder to images (i.e. defines a distribution over images which is conditioned on the distribution of codes).
* Differences to variational autoencoders:
* Encoder and decoder are both recurrent neural networks.
* The encoder receives the previous output of the decoder.
* The decoder writes several times to the image array (instead of only once).
* The encoder has an attention mechanism. It can make a decision about the read location in the input image.
* The decoder has an attention mechanism. It can make a decision about the write location in the output image.
* 2.1 Network architecture
* They use LSTMs for the encoder and decoder.
* The encoder generates a vector.
* The decoder generates a vector.
* The encoder receives at each time step the image and the output of the previous decoding step.
* The hidden layer in between encoder and decoder is a distribution Q(Zt|ht^enc), which is a diagonal gaussian.
* The mean and standard deviation of that gaussian is derived from the encoder's output vector with a linear transformation.
* Using a gaussian instead of a bernoulli distribution enables the use of the reparameterization trick. That trick makes it straightforward to backpropagate "low variance stochastic gradients of the loss function through the latent distribution".
* The decoder writes to an image canvas. At every timestep the vector generated by the decoder is added to that canvas.
* 2.2 Loss function
* The main loss function is the negative log probability: `-log D(x|ct)`, where `x` is the input image and `ct` is the final output image of the autoencoder. `D` is a bernoulli distribution if the image is binary (only 0s and 1s).
* The model also uses a latent loss for the latent layer (between encoder and decoder). That is typical for VAEs. The loss is the KL-Divergence between Q(Zt|ht_enc) (`Zt` = latent layer, `ht_enc` = result of encoder) and a prior `P(Zt)`.
* The full loss function is the expection value of both losses added up.
* 2.3 Stochastic Data Generation
* To generate images, samples can be picked from the latent layer based on a prior. These samples are then fed into the decoder. That is repeated for several timesteps until the image is finished.
* 3. Read and Write Operations
* 3.1 Reading and writing without attention
* Without attention, DRAW simply reads in the whole image and modifies the whole output image canvas at every timestep.
* 3.2 Selective attention model
* The model can decide which parts of the image to read, i.e. where to look at. These looks are called glimpses.
* Each glimpse is defined by its center (x, y), its stride (zoom level), its gaussian variance (the higher the variance, the more blurry is the result) and a scalar multiplier (that scales the intensity of the glimpse result).
* These parameters are calculated based on the decoder output using a linear transformation.
* For an NxN patch/glimpse `N*N` gaussians are created and applied to the image. The center pixel of each gaussian is then used as the respective output pixel of the glimpse.
* 3.3 Reading and writing with attention
* Mostly the same technique from (3.2) is applied to both reading and writing.
* The glimpse parameters are generated from the decoder output in both cases. The parameters can be different (i.e. read and write at different positions).
* For RGB the same glimpses are applied to each channel.
* 4. Experimental results
* They train on binary MNIST, cluttered MNIST, SVHN and CIFAR-10.
* They then classfiy the images (cluttered MNIST) or generate new images (other datasets).
* They say that these generated images are unique (to which degree?) and that they look realistic for MNIST and SVHN.
* Results on CIFAR-10 are blurry.
* They use binary crossentropy as the loss function for binary MNIST.
* They use crossentropy as the loss function for SVHN and CIFAR-10 (color).
* They used Adam as their optimizer.
* 4.1 Cluttered MNIST classification
* They classify images of cluttered MNIST. To do that, they use an LSTM that performs N read-glimpses and then classifies via a softmax layer.
* Their model's error rate is significantly below a previous non-differentiable attention based model.
* Performing more glimpses seems to decrease the error rate further.
* 4.2 MNIST generation
* They generate binary MNIST images using only the decoder.
* DRAW without attention seems to perform similarly to previous models.
* DRAW with attention seems to perform significantly better than previous models.
* DRAW without attention progressively sharpens images.
* DRAW with attention draws lines by tracing them.
* 4.3 MNIST generation with two digits
* They created a dataset of 60x60 images, each of them containing two random 28x28 MNIST images.
* They then generated new images using only the decoder.
* DRAW learned to do that.
* Using attention, the model usually first drew one digit then the other.
* 4.4 Street view house number generation
* They generate SVHN images using only the decoder.
* Results look quite realistic.
* 4.5 Generating CIFAR images
* They generate CIFAR-10 images using only the decoder.
* Results follow roughly the structure of CIFAR-images, but look blurry.
 |
Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks
Denton, Emily L. and Chintala, Soumith and Szlam, Arthur and Fergus, Rob
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
Denton, Emily L. and Chintala, Soumith and Szlam, Arthur and Fergus, Rob
Neural Information Processing Systems Conference - 2015 via Local Bibsonomy
Keywords: dblp
|
[link]
* The original GAN approach used one Generator (G) to generate images and one Discriminator (D) to rate these images.
* The laplacian pyramid GAN uses multiple pairs of G and D.
* It starts with an ordinary GAN that generates small images (say, 4x4).
* Each following pair learns to generate plausible upscalings of the image, usually by a factor of 2. (So e.g. from 4x4 to 8x8.)
* This scaling from coarse to fine resembles a laplacian pyramid, hence the name.
### How
* The first pair of G and D is just like an ordinary GAN.
* For each pair afterwards, G recieves the output of the previous step, upscaled to the desired size. Due to the upscaling, the image will be blurry.
* G has to learn to generate a plausible sharpening of that blurry image.
* G outputs a difference image, not the full sharpened image.
* D recieves the upscaled/blurry image. D also recieves either the optimal difference image (for images from the training set) or G's generated difference image.
* D adds the difference image to the blurry image as its first step. Afterwards it applies convolutions to the image and ends in one sigmoid unit.
* The training procedure is just like in the ordinary GAN setting. Each upscaling pair of G and D can be trained on its own.
* The first G recieves a "normal" noise vector, just like in the ordinary GAN setting. Later Gs recieve noise as one plane, so each image has four channels: R, G, B, noise.
### Results
* Images are rated as looking more realistic than the ones from ordinary GANs.
* The approximated log likelihood is significantly lower (improved) compared to ordinary GANs.
* The generated images do however still look distorted compared to real images.
* They also tried to add class conditional information to G and D (just a one hot vector for the desired class of the image). G and D learned successfully to adapt to that information (e.g. to only generate images that seem to show birds).
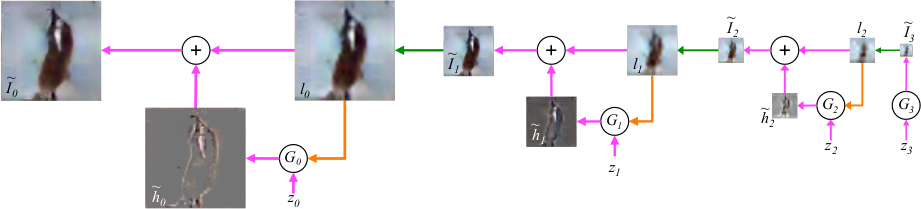
*Basic training and sampling process. The first image is generated directly from noise. Everything afterwards is de-blurring of upscaled images.*
-------------------------
### Rough chapter-wise notes
* Introduction
* Instead of just one big generative model, they build multiple ones.
* They start with one model at a small image scale (e.g. 4x4) and then add multiple generative models that increase the image size (e.g. from 4x4 to 8x8).
* This scaling from coarse to fine (low frequency to high frequency components) resembles a laplacian pyramid, hence the name of the paper.
* Related Works
* Types of generative image models:
* Non-Parametric: Models copy patches from training set (e.g. texture synthesis, super-resolution)
* Parametric: E.g. Deep Boltzmann machines or denoising auto-encoders
* Novel approaches: e.g. DRAW, diffusion-based processes, LSTMs
* This work is based on (conditional) GANs
* Approach
* They start with a Gaussian and a Laplacian pyramid.
* They build the Gaussian pyramid by repeatedly decreasing the image height/width by 2: [full size image, half size image, quarter size image, ...]
* They build a Laplacian pyramid by taking pairs of images in the gaussian pyramid, upscaling the smaller one and then taking the difference.
* In the laplacian GAN approach, an image at scale k is created by first upscaling the image at scale k-1 and then adding a refinement to it (de-blurring). The refinement is created with a GAN that recieves the upscaled image as input.
* Note that the refinement is a difference image (between the upscaled image and the optimal upscaled image).
* The very first (small scale) image is generated by an ordinary GAN.
* D recieves an upscaled image and a difference image. It then adds them together to create an upscaled and de-blurred image. Then D applies ordinary convolutions to the result and ends in a quality rating (sigmoid).
* Model Architecture and Training
* Datasets: CIFAR-10 (32x32, 100k images), STL (96x96, 100k), LSUN (64x64, 10M)
* They use a uniform distribution of [-1, 1] for their noise vectors.
* For the upscaling Generators they add the noise as a fourth plane (to the RGB image).
* CIFAR-10: 8->14->28 (height/width), STL: 8->16->32->64->96, LSUN: 4->8->16->32->64
* CIFAR-10: G=3 layers, D=2 layers, STL: G=3 layers, D=2 layers, LSUN: G=5 layers, D=3 layers.
* Experiments
* Evaluation methods:
* Computation of log-likelihood on a held out image set
* They use a Gaussian window based Parzen estimation to approximate the probability of an image (note: not very accurate).
* They adapt their estimation method to the special case of the laplacian pyramid.
* Their laplacian pyramid model seems to perform significantly better than ordinary GANs.
* Subjective evaluation of generated images
* Their model seems to learn the rough structure and color correlations of images to generate.
* They add class conditional information to G and D. G indeed learns to generate different classes of images.
* All images still have noticeable distortions.
* Subjective evaluation of generated images by other people
* 15 volunteers.
* They show generated or real images in an interface for 50-2000ms. Volunteer then has to decide whether the image is fake or real.
* 10k ratings were collected.
* At 2000ms, around 50% of the generated images were considered real, ~90 of the true real ones and <10% of the images generated by an ordinary GAN.
 |
Mask R-CNN
He, Kaiming and Gkioxari, Georgia and Dollár, Piotr and Girshick, Ross B.
arXiv e-Print archive - 2017 via Local Bibsonomy
Keywords: dblp
He, Kaiming and Gkioxari, Georgia and Dollár, Piotr and Girshick, Ross B.
arXiv e-Print archive - 2017 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a variation of Faster R-CNN.
* Their network detects bounding boxes (e.g. of people, cars) in images *and also* segments the objects within these bounding boxes (i.e. classifies for each pixel whether it is part of the object or background).
* The model runs roughly at the same speed as Faster R-CNN.
### How
* The architecture and training is mostly the same as in Faster R-CNN:
* Input is an image.
* The *backbone* network transforms the input image into feature maps. It consists of convolutions, e.g. initialized with ResNet's weights.
* The *RPN* (Region Proposal Network) takes the feature maps and classifies for each location whether there is a bounding box at that point (with some other stuff to regress height/width and offsets).
This leads to a large number of bounding box candidates (region proposals) per image.
* *RoIAlign*: Each region proposal's "area" is extracted from the feature maps and converted into a fixed-size `7x7xF` feature map (with F input filters). (See below.)
* The *head* uses the region proposal's features to perform
* Classification: "is the bounding box of a person/car/.../background"
* Regression: "bounding box should have width/height/offset so and so"
* Segmentation: "pixels so and so are part of this object's mask"
* Rough visualization of the architecture:
* 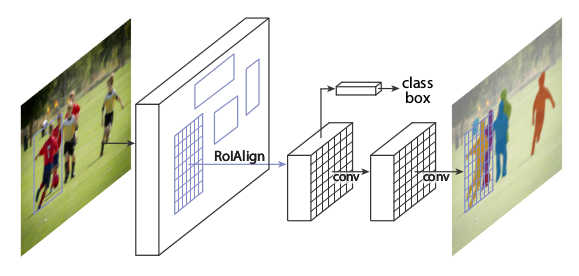
* RoIAlign
* This is very similar to RoIPooling in Faster R-CNN.
* For each RoI, RoIPooling first "finds" the features in the feature maps that lie within the RoI's rectangle. Then it max-pools them to create a fixed size vector.
* Problem: The coordinates where an RoI starts and ends may be non-integers. E.g. the top left corner might have coordinates `(x=2.5, y=4.7)`.
RoIPooling simply rounds these values to the nearest integers (e.g. `(x=2, y=5)`).
But that can create pooled RoIs that are significantly off, as the feature maps with which RoIPooling works have high (total) stride (e.g. 32 pixels in standard ResNets).
So being just one cell off can easily lead to being 32 pixels off on the input image.
* For classification, being some pixels off is usually not that bad. For masks however it can significantly worsen the results, as these have to be pixel-accurate.
* In RoIAlign this is compensated by not rounding the coordinates and instead using bilinear interpolation to interpolate between the feature map's cells.
* Each RoI is pooled by RoIAlign to a fixed sized feature map of size `(H, W, F)`, with H and W usually being 7 or 14. (It can also generate different sizes, e.g. `7x7xF` for classification and more accurate `14x14xF` for masks.)
* If H and W are `7`, this leads to `49` cells within each plane of the pooled feature maps.
* Each cell again is a rectangle -- similar to the RoIs -- and pooled with bilinear interpolation.
More exactly, each cell is split up into four sub-cells (top left, top right, bottom right, bottom left).
Each of these sub-cells is pooled via bilinear interpolation, leading to four values per cell.
The final cell value is then computed using either an average or a maximum over the four sub-values.
* Segmentation
* They add an additional branch to the *head* that gets pooled RoI as inputs and processes them seperately from the classification and regression (no connections between the branches).
* That branch does segmentation. It is fully convolutional, similar to many segmentation networks.
* The result is one mask per class.
* There is no softmax per pixel over the classes, as classification is done by a different branch.
* Base networks
* Their *backbone* networks are either ResNet or ResNeXt (in the 50 or 102 layer variations).
* Their *head* is either the fourth/fifth module from ResNet/ResNeXt (called *C4* (fourth) or *C5* (fifth)) or they use the second half from the FPN network (called *FPN*).
* They denote their networks via `backbone-head`, i.e. ResNet-101-FPN means that their backbone is ResNet-101 and their head is FPN.
* Visualization of the different heads:
* 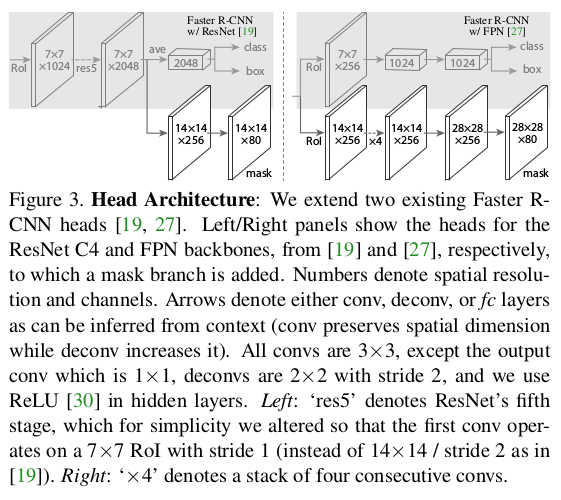
* Training
* Training happens in basically the same way as Faster R-CNN.
* They just add an additional loss term to the total loss (`L = L_classification + L_regression + L_mask`). `L_mask` is based on binary cross-entropy.
* For each predicted RoI, the correct mask is the intersection between that RoI's area and the correct mask.
* They only train masks for RoIs that are positive (overlap with ground truth bounding boxes).
* They train for 120k iterations at learning rate 0.02 and 40k at 0.002 with weight decay 0.0002 and momentum 0.9.
* Test
* For the *C4*-head they sample up to 300 region proposals from the RPN (those with highest confidence values). For the FPN head they sample up to 1000, as FPN is faster.
* They sample masks only for the 100 proposals with highest confidence values.
* Each mask is turned into a binary mask using a threshold of 0.5.
### Results
* Instance Segmentation
* They train and test on COCO.
* They can outperform the best competitor by a decent margin (AP 37.1 vs 33.6 for FCIS+++ with OHEM).
* Their model especially performs much better when there is overlap between bounding boxes.
* Ranking of their models: ResNeXt-101-FPN > ResNet-101-FPN > ResNet-50-FPN > ResNet-101-C4 > ResNet-50-C4.
* Using sigmoid instead of softmax (over classes) for the mask prediction significantly improves results by 5.5 to 7.1 points AP (depending on measurement method).
* Predicting only one mask per RoI (class-agnostic) instead of C masks (where C is the number of classes) only has a small negative effect on AP (about 0.6 points).
* Using RoIAlign instead of RoIPooling has significant positive effects on the AP of around 5 to 10 points (if a network with C5 head is chosen, which has a high stride of 32). Effects are smaller for small strides and FPN head.
* Using fully convolutional networks for the mask branch performs better than fully connected layers (1-3 points AP).
* Examples results on COCO vs FCIS (note the better handling of overlap):
* 
* Bounding-Box-Detection
* Training additionally on masks seems to improve AP for bounding boxes by around 1 point (benefit from multi-task learning).
* Timing
* Around 200ms for ResNet-101-FPN. (M40 GPU)
* Around 400ms for ResNet-101-C4.
* Human Pose Estimation
* The mask branch can be used to predict keypoint (landmark) locations on human bodies (i.e. locations of hands, feet etc.).
* This is done by using one mask per keypoint, initializing it to `0` and setting the keypoint location to `1`.
* By doing this, Mask R-CNN can predict keypoints roughly as good as the current leading models (on COCO), while running at 5fps.
* Cityscapes
* They test their model on the cityscapes dataset.
* They beat previous models with significant margins. This is largely due to their better handling of overlapping instances.
* They get their best scores using a model that was pre-trained on COCO.
* Examples results on cityscapes:
* 
 |
MobileNets: Efficient Convolutional Neural Networks for Mobile Vision Applications
Howard, Andrew G. and Zhu, Menglong and Chen, Bo and Kalenichenko, Dmitry and Wang, Weijun and Weyand, Tobias and Andreetto, Marco and Adam, Hartwig
arXiv e-Print archive - 2017 via Local Bibsonomy
Keywords: dblp
Howard, Andrew G. and Zhu, Menglong and Chen, Bo and Kalenichenko, Dmitry and Wang, Weijun and Weyand, Tobias and Andreetto, Marco and Adam, Hartwig
arXiv e-Print archive - 2017 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a factorization of standard 3x3 convolutions that is more efficient.
* They build a model based on that factorization. The model has hyperparameters to choose higher performance or higher accuracy.
### How
* Factorization
* They factorize the standard 3x3 convolution into one depthwise 3x3 convolution, followed by a pointwise convoluton.
* Normal 3x3 convolution:
* Computes per filter and location a weighted average over all filters.
* For kernel height `kH`, width `kW` and number of input filters/planes `Fin`, it requires `kH*kW*Fin` computations per location.
* Depthwise 3x3 convolution:
* Computes per filter and location a weighted average over *one* input filter. E.g. the 13th filter would only computed weighted averages over the 13th input filter/plane and ignore all the other input filters/planes.
* This requires `kH*kW*1` computations per location, i.e. drastically less than a normal convolution.
* Pointwise convolution:
* This is just another name for a normal 1x1 convolution.
* This is placed after a depthwise convolution in order to compensate the fact that every (depthwise) filter only sees a single input plane.
* As the kernel size is `1`, this is rather fast to compute.
* Visualization of normal vs factorized convolution:
* 
* Models
* They use two hyperparameters for their models.
* `alpha`: Multiplier for the width in the range `(0, 1]`. A value of 0.5 means that every layer has half as many filters.
* `roh`: Multiplier for the resolution. In practice this is simply the input image size, having a value of `{224, 192, 160, 128}`.
### Results
* ImageNet
* Compared to VGG16, they achieve 1 percentage point less accuracy, while using only about 4% of VGG's multiply and additions (mult-adds) and while using only about 3% of the parameters.
* Compared to GoogleNet, they achieve about 1 percentage point more accuracy, while using only about 36% of the mult-adds and 61% of the parameters.
* Note that they don't compare to ResNet.
* Results for architecture choices vs. accuracy on ImageNet:
* 
* Relation between mult-adds and accuracy on ImageNet:
* 
* Object Detection
* Their mAP is a bit on COCO when combining MobileNet with SSD (as opposed to using VGG or Inception v2).
* Their mAP is quite a bit worse on COCO when combining MobileNet with Faster R-CNN.
* Reducing the number of filters (`alpha`) influences the results more than reducing the input image resolution (`roh`).
* Making the models shallower influences the results more than making them thinner.
 |
SSD: Single Shot MultiBox Detector
Liu, Wei and Anguelov, Dragomir and Erhan, Dumitru and Szegedy, Christian and Reed, Scott E. and Fu, Cheng-Yang and Berg, Alexander C.
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
Liu, Wei and Anguelov, Dragomir and Erhan, Dumitru and Szegedy, Christian and Reed, Scott E. and Fu, Cheng-Yang and Berg, Alexander C.
European Conference on Computer Vision - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a new bounding box detector.
* Their detector works without an RPN and RoI-Pooling, making it very fast (almost 60fps).
* Their detector works at multiple scales, making it better at detecting small and large objects.
* They achieve scores similar to Faster R-CNN.
### How
* Architecture
* Similar to Faster R-CNN, they use a base network (modified version of VGG16) to transform images to feature maps.
* They do not use an RPN.
* They predict via convolutions for each location in the feature maps:
* (a) one confidence value per class (high confidence indicates that there is a bounding box of that class at the given location)
* (b) x/y offsets that indicate where exactly the center of the bounding box is (e.g. a bit to the left or top of the feature map cell's center)
* (c) height/width values that reflect the (logarithm of) the height/width of the bounding box
* Similar to Faster R-CNN, they also use the concept of anchor boxes.
So they generate the described values not only once per location, but several times for several anchor boxes (they use six anchor boxes).
Each anchor box has different height/width and optionally scale.
* Visualization of the predictions and anchor boxes:
* 
* They generate these predictions not only for the final feature map, but also for various feature maps in between (e.g. before pooling layers).
This makes it easier for the network to detect small (as well as large) bounding boxes (multi-scale detection).
* Visualization of the multi-scale architecture:
* 
* Training
* Ground truth bounding boxes have to be matched with anchor boxes (at multiple scales) to determine correct outputs.
To do this, anchor boxes and ground truth bounding boxes are matched if their jaccard overlap is 0.5 or higher.
Any unmatched ground truth bounding box is matched to the anchor box with highest jaccard overlap.
* Note that this means that a ground truth bounding box can be assigned to multiple anchor boxes (in Faster R-CNN it is always only one).
* The loss function is similar to Faster R-CNN, i.e. a mixture of confidence loss (classification) and location loss (regression).
They use softmax with crossentropy for the confidence loss and smooth L1 loss for the location.
* Similar to Faster R-CNN, they perform hard negative mining.
Instead of training every anchor box at every scale they only train the ones with the highest loss (per example image).
While doing that, they also pick the anchor boxes to be trained so that 3 in 4 boxes are negative examples (and 1 in 4 positive).
* Data Augmentation: They sample patches from images using a wide range of possible sizes and aspect ratios.
They also horizontally flip images, perform cropping and padding and perform some photo-metric distortions.
* Non-Maximum-Suppression (NMS)
* Upon inference, they remove all bounding boxes that have a confidence below 0.01.
* They then apply NMS, removing bounding boxes if there is already a similar one (measured by jaccard overlap of 0.45 or more).
### Results
* Pascal VOC 2007
* They achieve around 1-3 points mAP better results than Faster R-CNN.
* 
* Despite the multi-scale method, the model's performance is still significantly worse for small objects than for large ones.
* Adding data augmentation significantly improved the results compared to no data augmentation (around 6 points mAP).
* Using more than one anchor box also had noticeable effects on the results (around 2 mAP or more).
* Using multiple feature maps to predict outputs (multi-scale architecture) significantly improves the results (around 10 mAP).
Though adding very coarse (high-level) feature maps seems to rather hurt than help.
* Pascal VOC 2012
* Around 4 mAP better results than Faster R-CNN.
* COCO
* Between 1 and 4 mAP better results than Faster R-CNN.
* Times
* At a batch size of 1, SSD runs at about 46 fps at input resolution 300x300 (74.3 mAP on Pascal VOC) and 19 fps at input resolution 512x512 (76.8 mAP on Pascal VOC).
* 

1 Comments
|
Feature Pyramid Networks for Object Detection
Lin, Tsung-Yi and Dollár, Piotr and Girshick, Ross B. and He, Kaiming and Hariharan, Bharath and Belongie, Serge J.
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
Lin, Tsung-Yi and Dollár, Piotr and Girshick, Ross B. and He, Kaiming and Hariharan, Bharath and Belongie, Serge J.
arXiv e-Print archive - 2016 via Local Bibsonomy
Keywords: dblp
|
[link]
* They suggest a modified network architecture for object detectors (i.e. bounding box detectors).
* The architecture aggregates features from many scales (i.e. before each pooling layer) to detect both small and large object.
* The network is shaped similar to an hourglass.
### How
* Architecture
* They have two branches.
* The first one is similar to any normal network:
Convolutions and pooling.
The exact choice of convolutions (e.g. how many) and pooling is determined by the used base network (e.g. ~50 convolutions with ~5x pooling in ResNet-50).
* The second branch starts at the first one's output.
It uses nearest neighbour upsampling to re-increase the resolution back to the original one.
It does not contain convolutions.
All layers have 256 channels.
* There are connections between the layers of the first and second branch.
These connections are simply 1x1 convolutions followed by an addition (similar to residual connections).
Only layers with similar height and width are connected.
* Visualization:
* 
* Integration with Faster R-CNN
* They base the RPN on their second branch.
* While usually an RPN is applied to a single feature map of one scale, in their case it is applied to many feature maps of varying scales.
* The RPN uses the same parameters for all scales.
* They use anchor boxes, but only of different aspect ratios, not of different scales (as scales are already covered by their feature map heights/widths).
* Ground truth bounding boxes are associated with the best matching anchor box (i.e. one box among all scales).
* Everything else is the same as in Faster R-CNN.
* Integration with Fast R-CNN
* Fast R-CNN does not use an RPN, but instead usually uses Selective Search to find region proposals (and applies RoI-Pooling to them).
* Here, they simply RoI-Pool from the FPN's output of the second branch.
* They do not pool over all scales. Instead they pick only the scale/layer that matches the region proposal's size (based on its height/width).
* They process each pooled RoI using two 1024-dimensional fully connected layers (initalizes randomly).
* Everything else is the same as in Fast R-CNN.
### Results
* Faster R-CNN
* FPN improves recall on COCO by about 8 points, compared to using standard RPN.
* Improvement is stronger for small objects (about 12 points).
* For some reason no AP values here, only recall.
* The RPN uses some convolutions to transform each feature map into region proposals.
Sharing the features of these convolutions marginally improves results.
* Fast R-CNN
* FPN improves AP on COCO by about 2 points.
* Improvement is stronger for small objects (about 2.1 points).
 |












