Temporal Cycle-Consistency Learning
Dwibedi, Debidatta and Aytar, Yusuf and Tompson, Jonathan and Sermanet, Pierre and Zisserman, Andrew
arXiv e-Print archive - 2019 via Local Bibsonomy
Keywords: dblp
Dwibedi, Debidatta and Aytar, Yusuf and Tompson, Jonathan and Sermanet, Pierre and Zisserman, Andrew
arXiv e-Print archive - 2019 via Local Bibsonomy
Keywords: dblp
|
[link]
# Overview This paper presents a novel way to align frames in videos of similar actions temporally in a self-supervised setting. To do so, they leverage the concept of cycle-consistency. They introduce two formulations of cycle-consistency which are differentiable and solvable using standard gradient descent approaches. They name their method Temporal Cycle Consistency (TCC). They introduce a dataset that they use to evaluate their approach and show that their learned embeddings allow for few shot classification of actions from videos. Figure 1 shows the basic idea of what the paper aims to achieve. Given two video sequences, they wish to map the frames that are closest to each other in both sequences. The beauty here is that this "closeness" measure is defined by nearest neighbors in an embedding space, so the network has to figure out for itself what being close to another frame means. The cycle-consistency is what makes the network converge towards meaningful "closeness".  # Cycle Consistency Intuitively, the concept of cycle-consistency can be thought of like this: suppose you have an application that allows you to take the photo of a user X and increase their apparent age via some transformation F and decrease their age via some transformation G. The process is cycle-consistent if you can age your image, then using the aged image, "de-age" it and obtain something close to the original image you took; i.e. F(G(X)) ~= X. In this paper, cycle-consistency is defined in the context of nearest-neighbors in the embedding space. Suppose you have two video sequences, U and V. Take a frame embedding from U, u_i, and find its nearest neighbor in V's embedding space, v_j. Now take the frame embedding v_j and find its closest frame embedding in U, u_k, using a nearest-neighbors approach. If k=i, the frames are cycle consistent. Otherwise, they are not. The authors seek to maximize cycle consistency across frames. # Differentiable Cycle Consistency The authors present two differentiable methods for cycle-consistency; cycle-back classification and cycle-back regression. In order to make their cycle-consistency formulation differentiable, the authors use the concept of soft nearest neighbor: 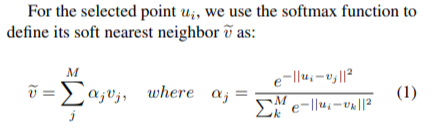 ## cycle-back classification Once the soft nearest neighbor v~ is computed, the euclidean distance between v~ and all u_k is computed for a total of N frames (assume N frames in U) in a logit vector x_k and softmaxed to a prediction ŷ = softmax(x): 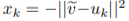. 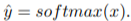 Note the clever use of the negative, which will ensure the softmax selects for the highest distance. The ground truth label is a one-hot vector of size 1xN where position i is set to 1 and all others are set to 0. Cross-entropy is then used to compute the loss. ## cycle-back regression The concept is very similar to cycle-back classification up to the soft nearest neighbor calculation. However the similarity metric of v~ back to u_k is not computed using euclidean distance but instead soft nearest neighbor again: 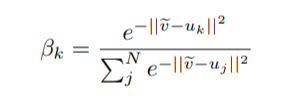 The idea is that they want to penalize the network less for "close enough" guesses. This is done by imposing a gaussian prior on beta centered around the actual closest neighbor i. 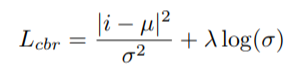 The following figure summarizes the pipeline: 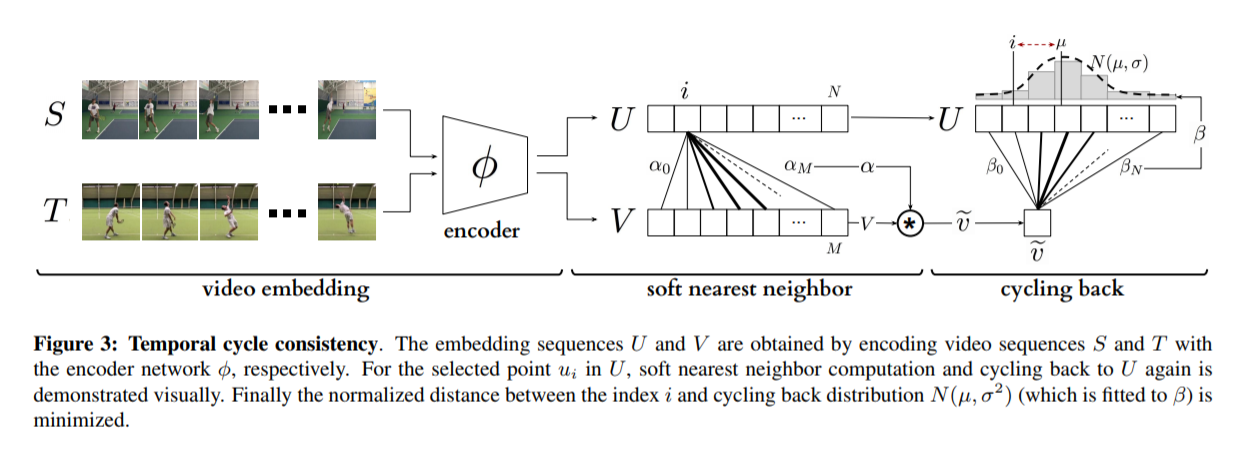 # Datasets All training is done in a self-supervised fashion. To evaluate their methods, they annotate the Pouring dataset, which they introduce and the Penn Action dataset. To annotate the datasets, they limit labels to specific events and phases between phases  # Model The network consists of two parts: an encoder network and an embedder network. ## Encoder They experiment with two encoders: * ResNet-50 pretrained on imagenet. They use conv_4 layer's output which is 14x14x1024 as the encoder scheme. * A Vgg-like model from scratch whose encoder output is 14x14x512. ## Embedder They then fuse the k following frame encodings along the time dimension, and feed it to an embedder network which uses 3D Convolutions and 3D pooling to reduce it to a 1x128 feature vector. They find that k=2 works pretty well.  |
You must log in before you can submit this summary! Your draft will not be saved!
Preview:












